Н.Ф. Мусаева, Д.И. Масталиева, Р.М. Кадымов
РЕШЕНИЕ ЗАДАЧИ КОНФЛЮЭНТНОГО АНАЛИЗА С ПОМОЩЬЮ РОБАСТНЫХ ОЦЕНОК ЗАШУМЛЕННЫХ СИГНАЛОВ
Институт кибернетики НАНА, Баку, Азербайджан
musana@rambler.ru, musaeva@cyber.ab.az ,dilara.mestelieva@gmail.com, rauf_qadimov@mail.ru
Первоисточник http://www.science.az/cyber/pci2006/1/!1r12-musayeva.doc
Известно, что при построении математических моделей
общий вид исследуемой зависимости между выходной ![]() и
входными
и
входными ![]() ,
, ![]() переменными считается заданным, неизвестными
являются значения вектора коэффициентов
переменными считается заданным, неизвестными
являются значения вектора коэффициентов ![]() .
Так, например, при линейной форме зависимости следует найти значения
коэффициентов
.
Так, например, при линейной форме зависимости следует найти значения
коэффициентов ![]() уравнения:
уравнения:
![]() =
=![]() +
+![]() +
+![]() . (1)
. (1)
При традиционном подходе к решению этой задачи предполагается,
что выполняются классические ограничения [1, с. 22-26]. Это означает, что
выходной параметр ![]() и наложенная на нее помеха
и наложенная на нее помеха ![]() есть
случайные функции с нормальным законом распределения, помеха
есть
случайные функции с нормальным законом распределения, помеха ![]() имеет
нулевое математическое ожидание
имеет
нулевое математическое ожидание ![]() =0, некоррелированные значения
=0, некоррелированные значения 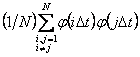 =0 и
одинаковые дисперсии
=0 и
одинаковые дисперсии ![]() ; входные параметры
; входные параметры ![]() ,
, ![]() , ...
,
, ...
, ![]() содержат пренебрежимо малые помехи; на значения коэффициентов модели
содержат пренебрежимо малые помехи; на значения коэффициентов модели
![]() ,
, ![]() =1,2,...,
=1,2,...,![]() не наложены никакие ограничения; ранг матрицы
входных переменных
не наложены никакие ограничения; ранг матрицы
входных переменных ![]() .
.
Однако по своей природе зависимости между выходным и входными переменными модели могут быть разделены на четыре группы [2, с. 210-220]: 1) детерминированные (тип А), когда исследуется функциональная зависимость между неслучайными выходной и входными переменными; 2) регрессионные (тип В), когда исследуется зависимость случайной выходной переменной от неслучайных входных переменных, причем входные переменные измеряются без ошибок и не содержат помех, а значения выходной переменной зависят от ряда случайных неконтролируемых помех; 3) корреляционные (тип С), когда исследуется зависимость между случайными выходной и входными переменными, причем входные переменные не содержат случайных помех; 4) конфлюэнтные (типы Д1 и Д2), когда исследуется функциональная зависимость между случайными или неслучайными переменными в ситуации, когда те и другие содержат некоторые случайные помехи.
В схемах Д1 и Д2 речь идет о восстановлении искомых зависимостей по искаженным наблюдениям анализируемых переменных, причем, в отличие от регрессионной схемы искаженными оказываются при наблюдении не только значения выходной переменной, но и значения входных переменных. В зависимости от того, между какими именно переменными - неслучайными или случайными – исследуются связи, имеют соответственно тип связи по схеме Д1 или Д2. Оба эти типа связей называются зависимостями по схеме конфлюэнтного анализа.
Существует множество конфлюэнтных методов, и они
весьма разнообразны [2, с. 210-220]. Однако для построения состоятельных
оценок, кроме результатов измерений входных ![]() и
выходного
и
выходного ![]() параметров, необходима дополнительная информация
о дисперсиях
параметров, необходима дополнительная информация
о дисперсиях ![]() ,
, ![]() помех
помех ![]() ,
, ![]() , которыми искажены соответственно
, которыми искажены соответственно ![]() ,
, ![]() ,
либо отношение этих дисперсий
,
либо отношение этих дисперсий ![]() /
/![]() . Только в том случае, когда известна одна из
дисперсий помех или их отношение, можно построить модификации оценок метода
наименьших квадратов (МНК), и они окажутся состоятельными. Но, к сожалению,
вычислить дисперсии помех, не поддающихся измерению, невозможно. Поэтому хорошо
разработанные конфлюэнтные методы типа Д2 оказываются практически непригодными
для построения адекватных математических моделей исследуемых технологических процессов.
. Только в том случае, когда известна одна из
дисперсий помех или их отношение, можно построить модификации оценок метода
наименьших квадратов (МНК), и они окажутся состоятельными. Но, к сожалению,
вычислить дисперсии помех, не поддающихся измерению, невозможно. Поэтому хорошо
разработанные конфлюэнтные методы типа Д2 оказываются практически непригодными
для построения адекватных математических моделей исследуемых технологических процессов.
В данной работе предлагается решение задачи конфлюэнтного анализа типа Д2 с помощью алгоритмов вычисления дисперсии помехи, величины робастности оценок авто и взаимно корреляционных функций, робастных оценок коэффициентов корреляции и уравновешивания величин относительных погрешностей элементов робастных корреляционных матриц, разработанных в предыдущих работах [3, с. 50-63; 4, с. 15-26; 5, с. 64-74]. Для этого предлагается следующий алгоритм (вычисления проводятся для дискретизированных сигналов):
1) вычисляются оценки авто и взаимно корреляционных функций центрированных и нецентрированных зашумленных входных и выходного сигналов:
![]() ,
, ![]() (6)
(6)
![]() , (7)
, (7)
![]() , (8)
, (8)
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() -
-![]() , (11)
, (11)
![]() =
=![]() -
-![]() ,
, ![]() =
=![]() -
-![]() ,
, ![]() ,
, ![]() – математические ожидания
– математические ожидания ![]() ,
,![]() ;
;
2) вычисляются робастные оценки авто и взаимно корреляционных функций:
 , (12)
, (12)
![]() , (13)
, (13)
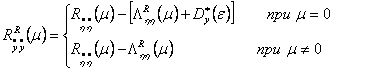 , (14)
, (14)
![]() , (15)
, (15)
где
![]() ,
,
![]() ,
,
![]() =
=![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() =
=![]() ,
,
![]() ,
,![]() ,
, ![]() ,
, ![]() =
=![]() ,
,
![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() –
количество положительных и отрицательных произведений
–
количество положительных и отрицательных произведений ![]() ,
, ![]() ,
, ![]() при
временном сдвиге
при
временном сдвиге ![]() ;
;
3) вычисляются робастные коэффициенты корреляции:
![]() =
=![]() /
/![]() ,
, ![]() (16)
(16)
![]() =
=![]() /
/![]() . (17)
. (17)
Для вычисления робастных коэффициентов модели необходимо сначала составить робастные корреляционные матрицы, то есть выполнить следующую работу:
1) составить робастную корреляционную матрицу из робастных оценок коэффициентов корреляции входных сигналов, а также вектор-столбец из робастных оценок коэффициентов корреляции между входными и выходным сигналами:
![]() =
= ; (18)
; (18)
![]() =
=![]() ; (19)
; (19)
2)
вычислить число обусловленности робастной корреляционной матрицы ![]() :
:
![]() =
=![]() ; (20)
; (20)
3)
заменить соответственно 1-й, 2-й, …, n-й столбцы
робастной корреляционной матрицы ![]() робастным вектором-столбцом
робастным вектором-столбцом ![]() , и
составить робастные матрицы:
, и
составить робастные матрицы:
![]() =
=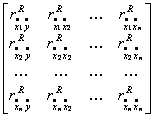 ;…,
;…,![]() =
= ; (21)
; (21)
4)
вычислить определители ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() робастных корреляционных матриц
робастных корреляционных матриц ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() ;
;
5) вычислить робастные коэффициенты математической модели:
![]() =
=![]() , …,
, …, ![]() =
=![]() ,
, ![]() , (22)
, (22)
где
![]() ,
, ![]() .
.
Для проверки эффективности технологии решения задач конфлюэнтного анализа с использованием робастных коэффициентов корреляции и робастных корреляционных матриц были проведены вычислительные эксперименты, которые показали, что разработанные технологии вычисления дисперсии помехи, величины робастности оценок авто и взаимно корреляционных функций, робастных оценок коэффициентов корреляции и уравновешивания величин относительных погрешностей элементов корреляционных матриц дают возможность решать задачи конфлюэнтного анализа и обеспечивать адекватность математических моделей исследуемых объектов контроля и управления.
Работа выполнена при поддержке Азербайджанского Национального Научного Фонда (Azerbaijan National Science Foundation (ANSF)) и Американского Фонда Гражданских Исследований и Развития (the U.S. Civilian Research & Development Foundation (CRDF)), грант N3104.
Литература
1. Вучков И., Бояджиева Л., Солаков Е. Прикладной линейный регрессионный анализ, М.: Финансы и статистика, 1987, 240 с.
2. Грановский В.А., Сирая Т.Н. Методы обработки экспериментальных данных при измерениях, Ленинград.: Энергоатомиздат, 1990, 288 с.
3. Мусаева Н.Ф. Робастный метод оценивания при “загрязнениях” грубыми ошибками // Автоматика и вычислительная техника, №6, 2003, с. 50-63.
4. Алиев Т.А., Мусаева Н.Ф. Технология экспериментального исследования стохастических процессов // Автоматика и вычислительная техника,№4, 2005, с.15-26.
5. Мусаева Н.Ф. Технология вычисления величины робастности как оценки статистической характеристики зашумленного сигнала // Автоматика и вычислительная техника, №5, 2005, с. 64-74.