Сравнительный анализ различных методов обнаружения грубых ошибок является акту­альным в теории и практике обработки геодезических измерений.Ниже анализи­руются два таких метода: по невязкам услов­ных уравнений и поправкам в результаты измерений [1,4]. Цель данной статьи — установить метод, позволяющий определять не только наличие грубой ошибки, но и измерение, в котором она допущена. Значение имеет также простота реализации метода в компьютерной программе. J) Рассмотрим условия, необходимые для обнаружения грубой ошибки по невязкам условных уравнений. Зависимость невязки w условного уравнения от ошибок из­мерений характеризуется уравнением

                                        (1)

где  — коэффициенты условного уравне­ния;

—ошибки измерений(i= 1,2, ...,n). Если ошибки случайны и их матема­тические ожидания равны нулю, то матема­тическое ожидание невязки тоже равно нулю, а возможный диапазон ее значений при равноточных измерениях характеризуется доверительным интервалом

                                                          

 

где  - стандарт измерения. При этом значение t определяет вероятность попадания невязки в соответствующий интервал. Зна­чение t = 2,5 считают предельным и для обнаружения грубых ошибок используют допуск

                                                   (2)

 

 

 

Предположим, что одно из измерений кроме обычной случайной ошибки со-г держит еще и грубую . Тогда

,

,

где h — номер коэффициента и соот­ветствующего ошибочного измерения.

Проанализируем, какое значение грубой ошибки  может быть обнаружено на фоне «шума», образуемого случайными ошибками . Заметим, что при любом фиксированном зна­чении . математическое ожидание  (обоз­начим его как среднее ) уже не равно нулю.

т. е. центр рассеяния возможных значений невязки смещен на величину , и дове­рительный интервал, в котором они могут оказаться, равен

Условие  применяемое для обнаружения грубой ошибки, на краях интервалов

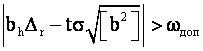
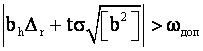
Таким образом, возможность обнаружения грубой ошибки  носит вероятностный характер и зависит от значений случайных ошибок.

Если при этом невязка окажется на нижней границе интервала, то с по­мощью допуска (2) может быть обнаружена грубая ошибка

 

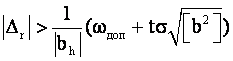                                               (3)

если на верхней,

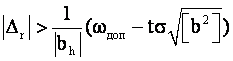                                               (4)

Неравенства (3) и (4) указывают с неко­торой вероятностью границы диапазона, в котором может быть обнаружена грубая ошибка. Смысл диапазона прост — при благоприятном стечении случайных ошибок грубая ошибка меньше, чем при небла­гоприятном.

Желая исследовать действие случайных ошибок при средних условиях измерений, положим, что их рассеивание соответствует стандарту , тогда в (3) и (4) t= 1. Заметим, что, исследуя условия, отличающиеся от средних, следует принять иное значение t. Для t=1 имеем

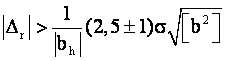
где знаки "+" и "—" соответствуют границам обнаружения грубой ошибки. Среднее ее значение соответствует положению, когда все ошибки, кроме грубой, равны нулю

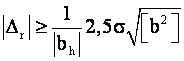
Например, по невязке условия фигуры в треугольнике, где коэффициент   а число их равно 6, грубая ошибка может быть обнаружена на интервале 3,0-8,5, где  средняя квадратическая ошибка нап­равления. Для полигона с  пятью вершинами диапазон обнаружения соответствует 4,7-11,1. Отметим, что,  используя вместо направлений углы, получим множители при  в    раза меньше, а обнаружения грубых ошибок по невязкам условий фигур не изменятся.

В условном уравнении полюса геоде­зического четырехугольника квадратной формы коэффициенты условного уравнения также равны 1 (°). Вычисляя нап­равления, найдем, что в этом случае , т. е. в среднем может быть обнаружена ошибка, превышающая . Границы ее обнаружения зависят от значений случайных ошибок. На основании вышесказанного можно сделать вывод, что по невязкам условных уравнений определяются только крупные промахи.

Исследуем возможности обнаружения грубых ошибок по поправкам. Векторы поправок V и ошибки измерений связаны формулой [2]

                                                (5)

 

причем корреляционная матрица поправок равна:

 

                                                                              (6)

где      -средняя квадратическая ошибка единицы веса;

            P – матрица весов измерений.

 

Матрица  находится по формуле:

                                                                         

где      E – единичная матрица;

            А – матрица коэффициентов параметрических уравнений поправок;

            N - матрица коэффициентов нормальных уравнений, которая находится по формуле:

 

                                                                              

С ростом ошибок измерений увеличиваются поправки, по значению которых можно судить о наличии грубых ошибок. Допуски для поправок вычисляют по формуле:

 

                                               

 

где       - параметр, обычно принимаемый 2,5;

 - средняя квадратическая ошибка поправки (корень из i-го диагонального элемента матрицы , которая находится по формуле (1.17).

Допуски для поправок вычисляется с учётом всех геометрических условий, связанных с i-м измерением. Чтобы обнаружить грубую ошибку, необходимо выполнение неравенства >. Пока­жем, что одновременный учет позволяет об­наруживать грубые ошибки меньшие, чем по невязкам   каждого условного уравнения.

Известно, что точность поправок повы­шается с увеличением избыточных измере­ний. При этом уменьшаются стандарты поправок и вычисляемые по ним допуски d, что позволяет обнаруживать меньшие грубые ошибки. Рассмотрим наихудший случай, когда число избыточных измерений минимально, т. е. равно 1. Считая из­мерения равноточными, по формулам коррелатного уравнивания найдем

 

;

 

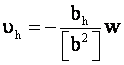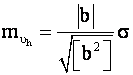
где обозначения те же, что и в (1).

Подстановка этих выражений в неравен­ство    приводит после преобра­зований к неравенству , т. е. к допуску (2). Следовательно, при наличии только одного избыточного измерения оба метода позволяют обнаруживать одинаковые грубые ошибки. При большем числе избыточных измерений допуски уменьшаются, и по поправкам из уравнивания обнаруживаются грубые ошибки меньшие, чем по невязкам ус­ловных уравнений.

Представим вектор ошибок измерений, содержащий грубую ошибку, как сумму двух слагаемых D^т = (D₁ D₂ ...D_h... D_n) + (0 0 ... D_r ... 0). Поправка к h-му измерению согласно (5)

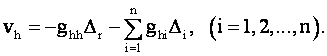
Допуск для этой поправки

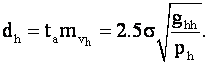                                        (7)

Чтобы обнаружить грубую ошибку, необходимо выполнение неравенства v_h > d_h.

Приняв случайные ошибки равными нулю, что соответствует средним условиям, найдём для модуля грубой ошибки сред­нюю границу её обнаружения

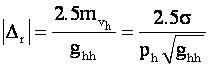                                        (8)

Например, в геодезическом четырёхугольнике (квадрате) допуски d_i равны 1,36 s для поправок крайних направлений на каждом пункте и 1,62 s — для диагональ­ных направлений. В соответствии с (7) в случае равенства весов (р_i - 1) получим для крайних направлений g_ii = 0,295 и средних — g_ii = 0,420. После этого по формуле (8) определим среднюю границу обнаружения грубой ошибки, которая соответствует 4,6 s для крайних нап­равлений, и 3,9 s для направлений ди­агоналей. Сравнение результатов с полу­ченными ранее также подтверждает, что по поправкам обнаруживаются меньшие грубые ошибки, чем по невязкам.

Исследуем теперь возможность иденти­фицировать грубую ошибку по значению поправок. Сомнение вызвано лишь тем, что в процессе уравнивания грубая ошибка влияет на все поправки, составляющие вектор V, изменяя их на величины g_ihD_r, где h — номер столбца матрицы G, совпадающий с но­мером ошибочного измерения; i = 1, 2,...n. При этом не всегда большая поправка среди превысивших допуски указывает на измере­ние с грубой ошибкой.

Рассмотрим закономерности формирования нормированной поправки / и пропорционального ей отношения поправка/допуск. Представим матрицу  в виде:

                         

 

На основании (1.17), полагая измерения независимыми, запишем:

 

            

 

Подставим последнее выражение в (5) и заменим случайные ошибки измерений их математическими ожиданиями, равными нулю. Получим математическое ожидание вектора поправок:

 

           

 

 

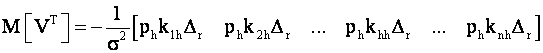
Допуски для поправок определяются формулой  (i= 1.2, .... n). Следовательно, отношение математического ожидания i-той поправки к допуску будет:

 

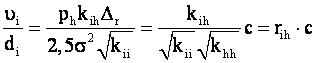                                               (9)

 

где      - коэффициент корреляции i-той и h-той поправок,

            постоянная .

 

Модули коэффициентов корреляции меньше либо равны единице для всех значений i. Следовательно, для измерения, содержащего грубую ошибку, отношение поправки к допуску имеет максимальное значение и может служить признаком для отбраковки этого измерения. Среди поправок, вышедших за границы допусков, грубая ошибка содержится в тех измерениях, где отношение модуля поправки к допуску наибольшее.

Конечно, наличие в результатах измере­ний фона из случайных ошибок несколько деформирует выведенные для матема­тических ожиданий соотношения, однако вследствие относительной малости этих ошибок установленная закономерность не нарушается, и метод надежно идентифицирует измерения с грубыми ошибками, что подтверждено экспериментальной проверкой на многочисленных сетях. После обнаружения измерения с грубой ошибкой его следует забраковать, а уравнивание выполнить вновь без него или первоначаль­ные результаты откорректировать по методике рекуррентного уравнивания [4].

Идентификация промахов, как и их обнаружение по поправкам эффективнее, чем по невязкам условных уравнений. В случаях, когда по невязке удается установить только наличие грубой ошибки (например, полигонометрический ход), максимум v/d точно указывает измерение, в котором она содер­жится. Отметим особый случай, когда иден­тификации измерения с грубой ошибкой препятствует равенство нескольких от­ношений v_i/d_i максимальному значению v_h/d_h. Это означает, что равны соответствующие коэффициенты корреляции r_ih = r_hh = ± 1 и, следовательно, существует тесная линейная взаимозависимость между i-й и h-й поправками. В этих условиях равнозначное изменение всех взаимозави­симых поправок может быть вызвано гру­бой ошибкой в любом из соответствующих измерений, и поэтому идентификация ошибочного измерения невозможна. Опи­санное равенство нескольких коэффици­ентов корреляции единице имеет место, например, для поправок в длины линий прямолинейного полигонометрического хода или в цепочке треугольников трилатерации. Но в подобных случаях иден­тификация вообще невозможна.

Сравним анализируемые методы по простоте их реализации в компьютерных программах. Известно, что построение программы для составления системы условных уравнений, отражающей все геометрические условия сети с учетом ее конкретных особенностей, представляет собой сложную задачу, решить которую в полной мере не удается [4, 5].

Параметрическое уравнивание с после­дующим поиском грубых ошибок по поп­равкам существенно проще. Указанный поиск требует вычисления диагональных элементов корреляционной матрицы К_v. Перепишем формулу (6) в виде

,

где К — корреляционная матрица ре­зультатов измерений; К_Х = s²N^-1 — кор­реляционная матрица уравненные пара­метров (координат пунктов). Для поиска грубых ошибок нужна не вся матрица К_v? а только ее диагональные элементы, вычисляемые по формуле

где m_i — средняя квадратическая ошибка i-го измерения; а_i — строка коэффициентов i-го параметрического уравнения поправок.

Как видим, алгоритм поиска грубых ошибок по поправкам очень прост, а необходимая для его реализации кор­реляционная матрица К_х, являющаяся одним из основных результатов уравни­вания, всегда имеется.

Исследуем возможность отыскания гру­бых ошибок, когда их несколько. Если одна из грубых ошибок значительно превышает остальные, она уверенно идентифицируется; соотношение (9) для нее оказывается наи­большим. При этом после отбраковки или исправления обнаруженного недоброкачест­венного измерения следует продолжить поиск меньших грубых ошибок.

Если грубые ошибки близки по зна­чению, идентификация измерений с про­махами может в принципе оказаться невозможной. Например, имея три направления, образующих два смежных угла, при наличии в двух из них ошибок, близких по значению, неизбежно придем к заключению об ошибочности третьего, верного направления, так как угол, об­разуемый ошибочными направлениями, будет лучше отвечать геометрическим ус­ловиям сети, чем углы, образуемые вер­ным направлением с ошибочными. Это заключение неизбежно, оно не зависит от применяемого для анализа сети метода, ибо другого критерия для поиска грубых ошибок, кроме внутренней сходимости результатов измерений, не существует.

Рассмотрим детальнее механизм фор­мирования поправок к результатам из­мерений при наличии в сети нескольких грубых ошибок. Пусть две грубые ошибки D_rg и D_rh допущены в g-м и h-м изме­рениях. Положим, что р_g = р_h = 1. Инте­ресующие нас элементы вектора V будут иметь вид

где v_g и v_h — математические ожидания поправок к g-му и h-му измерениям; v_i — математическое ожидание поправки к i-му доброкачественному измерению. Знаки «+» и «—» у ошибок D_rg и D_rh равновероятны, и нельзя предвидеть, где произведения будут суммироваться, а где вычитаться. При боль­ших корреляционных моментах k_ig и k_ih поправка v_i к i-му измерению может ока­заться существенно больше поправок v_g и v_h к измерениям с грубыми ошибками. Тогда верное i-е измерение будет идентифицироваться как ошибочное, независимо от метода. Заметим, что при увеличении числа избыточных измерений происходит достаточно быстрый рост диагональных элементов матрицы К_v и уменьшение корреляционных моментов, а следовательно уменьшение опасности неверной идентификации ошибочных измерений.

Для грубых ошибок, которые при благо­приятных условиях могут быть обнаружены, существует и теоретическая, граница [3]: их число ни при каких условиях не должно превышать числа избыточных измерений.

В заключение отметим, что установ­ленная неэффективность обнаружения грубых ошибок по невязкам условных уравнений относится к невязкам, вы­числяемым до уравнивания с целью при­менения в дальнейшем коррелатного способа или специально для обнаружения промахов. Более совершенный метод — использование невязок преобразованных условных уравнений рекуррентного урав­нивания [3] — в статье не исследуется.

 

 

СПИСОК ЛИТЕРАТУРЫ

1. Коугия В. А. Обнаружение грубых ошибок измерений по результатам уравнивания // Геодезия и картография – 1995, №6.— С. 14— 10

2. Линник Ю.В. Метод наименьших квадратов и основы матсматико-статистической теории обра­ботки наблюдений.— М.: Физматгиз. 1962.— 352 с.

3. Маркузе Ю.И. Уравнивание геодезических сетей с контролем грубых ошибок // Изв. вузов Сер. Геодезия и аэрофотосъемка. — 1986. - №5.— С. 9—18.