УДК 528.353.0 SS .2

© Б. Н. Дьяков. Ю. Б. Родионова, 2003

Тестирование линейно-угловых ходов на грубые ошибки измерений

Геодезия и картография. – 2003. - №7. – с. 21-24.

 

Проблема отыскания измерений, содер­жащих грубые ошибки, важна как с теоретической, так и с практической точки зрения. По нашему мнению, до­стоверность обнаружения грубой ошиб­ки в конкретном измерении во многом зависит от вида геодезического постро­ения. Для нивелирной сети, относящей­ся к одномерному пространству изме­рений, исследование методов поиска и учета грубых ошибок выполнено в дис­сертации Н. В. Федоровой, и результа­ты этого исследования частично опуб­ликованы*. В данной статье проблема поиска грубых ошибок рассматривается применительно к линейно-угловому хо­ду, относящемуся к двумерному про­странству измерений. И здесь, как вы­яснилось, существуют свои закономер­ности.

Известно, что в типовом разомкнутом линейно-угловом ходе имеются три из­быточных измерения независимо от числа сторон хода и его формы; в не­стандартном   ходе   их   может   быть   и меньше, и больше трех. Это обстоятель­ство ограничивает выбор методов для поиска грубых ошибок, так как должна быть предусмотрена возможность по­иска одной и более ошибок как в из­меренных углах, так и в сторонах. По­нятно, что применяемые на практике традиционные методы (отыскание одно­го ошибочно измеренного угла путем сравнения координат пунктов, вычис­ленных с начала и конца хода по фор­мулам висячего хода, или ошибочно измеренной стороны по дирекционному углу линейной невязки хода) являются малоэффективными. Неприменимыми в данном случае оказываются также дат­ский метод робастного оценивания и его модификации и метод .^-оценок, так как эти методы, оперируя поправками из уравнивания, совершенно не учитывают структуру G-матрицы геодезиче­ских построений, определяющую прави­ла формирования поправок. В частно­сти, во многих линейно-угловых ходах поправки в углы при исходных пунктах больше поправок в остальные углы не­зависимо от местонахождения грубых ошибок.

Нами разработаны два метода тести­рования геодезических построений на наличие в них грубых ошибок измере­ний: наложения графиков и исключения измерений.

 

 

Метод наложения графиков основан на использовании всех элементов G-матрицы. Если какое-либо измерение содержит грубую ошибку , то поправ­ки во все измерения вследствие этой ошибки  будут

                                                    (3.1)

где g_i,j — элементы j-го столбца G-матрицы.

 

Реальные поправки измерений V_i от­личаются от величин v_i,j, но эти отличия будут невелики, так как математиче­ское ожидание суммарного влияния ос­тальных случайных ошибок на каждую поправку в отдельности равно нулю. Чтобы выделить грубое измерение, до­статочно при вычисленном значении грубой ошибки j-го измерения   подсчитать для всех n измерений среднее квадратическое отклонение поправок V_i, от величин v_i,j по формуле

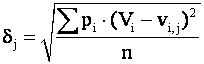                                                       (3.2)

После тестирования всех измерений грубым признается то, для которого значение    окажется наименьшим.

Для наглядности можно построить графики поправок из уравнивания V_i и величин v_i,j и наложить один на другой. Для грубого измерения совпадение гра­фиков будет наилучшим.

При тестировании на две грубые ошибки их предварительные значения  и    нужно   находить  из   решения системы двух уравнений [2], а среднее квадратическое отклонение  подсчи­тывать по формуле

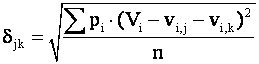                                         (3.3)

 

Для пары измерений, содержащих грубые ошибки, величина  должна иметь минимальное значение.

Метод последовательного уравнива­ния с исключением одного или несколь­ких измерений. Как известно, решаю­щим признаком наличия грубой ошибки в геодезическом построении является существенное увеличение ошибки еди­ницы веса  после уравнивания по сравнению с ее проектным значени­ем . Повторяя последовательно урав­нивание при одном исключенном изме­рении, можно найти такой вариант, в котором выполняется условие , и считать, что исключенное в этом ва­рианте измерение содержит грубую ошибку. Можно уравнивать сеть при двух исключенных измерениях, тогда в варианте и  оба исключенных из­мерения следует признать грубыми. Процесс можно продолжать при трех исключенных измерениях и т. д., пока не обнаружится  вариант .

Теоретически оба метода можно при­менять для отыскания (г - 1) грубых ошибок, где г — число избыточных из­мерений, поэтому в разомкнутом ли­нейно-угловом ходе возможен поиск пя­ти комбинаций  грубых ошибок:

одна  грубая ошибка в  угле;

одна грубая ошибка в стороне;

две грубые ошибки в углах;

две грубые ошибки в сторонах;

по одной грубой ошибке в угле и стороне.

Если угловая невязка хода не превы­шает допустимого значения, то первая и пятая комбинации отпадают (в третьей комбинации ошибки углов могут быть близки по величине и про­тивоположны по знаку).

С помощью программ, реализующих описанные выше методы тестирования геодезических построений, авторами статьи было выполнено исследование нескольких мо­делей разомкнутого линейно-углового хода разной длины, формы и точности. Необходимо отметить, что в программах предусмотрено вычисление поправок в грубые измерения. Одно или два изме­рения искажались грубыми ошибками, и выполнялся поиск ошибок по всем пяти комбинациям. Решение, соответ­ствующее искаженным измерениям, считалось главным, а все остальные — побочными. Некоторые результаты этих исследований приводятся ниже.

1. Одна грубая ошибка в любом угле обнаруживается в обоих методах; ми­нимумы величин  и  хорошо вы­ражены и фиксируются. При тестиро­вании ходов на третью и пятую ком­бинации минимумы фиксируются и для пар измерений, содержащих искомый угол, причем поправка во второе изме­рение любой такой комбинации равна нулю. Эти побочные решения подтвер­ждают главное решение. Кроме того, при тестировании хода произвольной формы (рис.3.1) на пятую комби­нацию грубые ошибки «обнаруживают­ся» в парах измерений, не содержащих искомого угла. Так, если ввести грубую ошибку в угол , то при полном тестировании хода получим сле­дующие результаты.

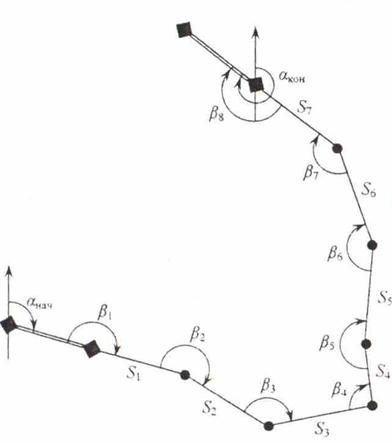
Рисунок 3.1 – Линейно-угловой ход произвольной формы

 

Грубая ошибка мо­жет содержаться в комбинациях: «угол », «угол  + любой другой угол», «угол  + любая сторона», « +», « +». Выявленные комбинации «грубых» ошибок в побочных решениях обладают полной реальностью; конт­рольное уравнивание хода с исправлен­ными «грубыми» измерениями дает хо­рошие показатели точности, но коорди­наты пунктов при этом получаются грубо ошибочными.

2. Две грубые ошибки в двух любых углах хода также обнаруживаются в обоих методах. При тестировании хода на пятую комбинацию ошибок миниму­мы величин  и  фиксируются и для  некоторых  пар  измерений,  не  содержащих грубых ошибок. Так, если ввести грубые ошибки в углы  и , то кроме главного решения в обоих методах фиксируются побочные реше­ния: « +», « +», « +». При изменении знака грубой ошибки в уг­ле  число побочных решений возра­стает.

3. Одна грубая ошибка в любой сто­роне хода произвольной формы обнару­живается по минимуму величин  и  однозначно, если в ходе нет других сторон, параллельных искомой стороне; в противном случае величины  и  получаются примерно одинаковыми для всех параллельных сторон. Кроме того, близкие к минимуму значения  и  фиксируются для некоторых комбинаций «угол + угол» (побочные решения).

4. Тестирование хода на две грубые ошибки в двух разных сторонах пока­зывает, что выявить эти ошибки в принципе невозможно. Для всех пар сторон величины  и  получаются одинаково малыми

5. Одна грубая ошибка в угле и одна в стороне обнаруживаются в обоих ме­тодах. Однако кроме искомой пары из­мерений минимумы величин  и  наблюдаются и для некоторых других пар измерений (двух углов или угла и стороны). Так, если ввести грубые ошибки, например, в угол  и сторо­ну  то по результатам тестирования грубые ошибки могут содержаться в комбинациях: « +», « +», « +», « +», « +», « +». При изменении знака грубой ошибки стороны ; все побочные решения ис­чезают.

6. Прямолинейный ход можно тести­ровать только на наличие грубых оши­бок в одном угле или в двух; грубые ошибки в сторонах такого хода обна­ружить невозможно.

Для нестандартного линейно-углового хода с дополнительными исходными пунктами все вышеприведенные выводы справедливы в пределах отдельных вет­вей хода между исходными пунктами. Независимо от числа ветвей в ходе с координатной привязкой грубые ошибки углов в крайних ветвях обнаружить не­возможно.

В предельно коротком линейно-угло­вом ходе, имеющем всего две непарал­лельные стороны и один определяемый пункт, уверенно обнаруживаются все пять комбинаций грубых ошибок. Этот факт позволяет рекомендовать для осо­бо ответственных объектов проектиро­вание линейно-угловых ходов, в кото­рых определяемые и исходные пункты чередуются.

При тестировании реального линей­но-углового хода с неизвестным распре-

делением ошибок рекомендуется выде­лять как потенциально грубые те из­мерения и пары измерений, для кото­рых величины  или  не превышают предела

 

,                                                              (3.4)

где n — общее число измерений в ходе;

г — число избыточных  измерений.

 

Если для всех измерений хода и их комбинаций величины  и   не пре­вышают , то в тестируемом ходе нет грубых ошибок. Если все значения  и  получились больше , то данный ход не соответствует проектному классу точности, должен быть переведен в по­ниженный класс или забракован.

Таким образом, следует признать, что в линейно-угловом ходе однозначно указать конкретные измерения, содер­жащие грубые ошибки, можно в отдель­ных частных случаях. В общем случае можно лишь сузить район поиска гру­бых ошибок до нескольких измерений.