Дьяков Б.Н., Федорова Н.В.

Пошаговый поиск грубых ошибок измерений // Геодезия и картография. – 2001. - №3. – с. 16-20

Суть метода в том, что произведение |pV| для измерения, содержащего грубую ошибку, больше такого же произведения для любого другого измерения, если в узловой точке их сходится больше двух. Этот критерий авторы статьи назвали pV-максимум.

Для того чтобы протестировать данную методику на способность обнаруживать 2 грубые ошибки и более, достаточно поставить условие пошагового поиска, при котором в пер­вом цикле обработки измерений лока­лизуется лишь одна грубая ошибка. Затем ее влияние устраняется, и выпол­няется второй цикл, в котором локали­зуется следующая грубая ошибка, и ус­траняется ее влияние. Циклы повторя­ются до тех пор, пока не будут обнаружены и локализованы все грубые ошибки. Понятно, что число грубых ошибок должно быть существенно мень­ше числа избыточных измерений [2].

Цель данной статьи — предложить еще один вариант поиска грубых ошибок измерений по поправкам из уравнивания, в котором не только определяются номера оши­бочных измерений, но и оценивается величина грубых ошибок.

Известно, что распределение истин­ных ошибок измерений по поправкам из уравнивания описывается матричным уравнением

                                            (2.1)

где Vn1 — вектор (матрица-столбец) по­правок из уравнивания размеромnxl;

Gnn — квадратная матрица эле­ментов g размером n х n;

— вектор (матрица-столбец) истинных ошибокизмерений размером n х 1;

n — число измерений сети. 

 

Матрица G имеет двойственную при­роду: с одной стороны, это матрица-преобразователь вектора  в вектор V(1); с другой — матрица-преобразова­тель матрицы обратных весов измере­ний Р^-1 в матрицу обратных весов по­правок

                                 Q_V=G Р^-1                                                        (2.2)

 

Формула (2.2) получается из формулы G = Q_V P после умножения ее спра­ва на Р^-1. При равноточных измерени­ях матрица Р превращается в единич­ную, a G — в матрицу обратных весов Qv

Будем использовать первое свойство матрицы G, которое можно детализировать так:

поправка какого-либо измерения V_i складывается из некоторой части истин­ной ошибки , этого же измерения и небольших долей истинных ошибок дру­гих измерений и выражается формулой

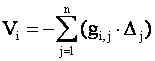                                            (2.3)

где g_i,j — коэффициент влияния истин­ной ошибки j-го измерения на поправку в i-e измерение.

 

В j-м столбце G-матрицы находятся коэффициенты влияния истинной ошиб­ки j-го измерения на поправки в каждое из n измерений.

i-я строка включает коэффициенты влияния на поправку j-го измерения истинных ошибок всех n измерений.

Авторы статьи проанализировали G-матрицы бо­лее двух десятков моделей геодезиче­ских построений, начиная с многократ­ных измерений одной величины и кон­чая системами линейно-угловых ходов с узловыми точками. В результате вы­явлено несколько закономерностей для сетей с однородными измерениями, одна из которых с полным правом может называться законом связи поправок в соседние измерения за счет ошибки од­ного из них. Этот закон звучит так: в пределах j-го столбца сумма произведений   для измерений пo линиям, сходящимся в узловой точке начала и конца j-й линии, равна про­изведению веса измерения по этой ли­нии на диагональный элемент j-го из­мерения

                                                        (2.4)

 

В равенстве (2.4) можно обойтись без знака «модуль», если направления всех линий, сходящихся в одной узловой точке с j-й линией, будут совпадать с ее направлением.

При истинной ошибке j-го измерения  её вклад в поправку i-го измерения

                                          (2.5)

 

Если в сети только одна ненулевая истинная ошибка  то

                           (2.6)

где V — поправки из уравнивания.

 

Из формулы (2.6) однозначно следует, что произведение |рV| для измерения, содержащего грубую ошибку, больше такого же произведения для любого другого измерения, если в узловой точ­ке сходится их больше двух. Это и есть критерий поиска грубой ошибки, кото­рый мы назвали РV-максимум.

Если в геодезической сети имеется несколько грубых ошибок, то после пер­вого   цикла   уравнивания   фиксируют первый максимум  произведения  |рV| и определяют номер измерения j.   Предполагая, что именно в этом измерении содержится грубая ошибка,  вычисляют ее приближенное значение по формуле

                                                    (2.7)

 

Результат j-го измерения исправляют на величину вычисленной грубой ошибки  и  уравнивают  сеть   второй   раз (отбраковывать   ошибочное   измерение нельзя, так как тогда изменится структура сети и придется пересчитывать не только G-матрицу, но и матрицу коэффициентов нормальных уравнений, корреляционную матрицу  поправок   и допуски на величину поправок в методике Коугия).   Проверяют  выполнение  двух условий:

 и                                        (2.8)

 

Если  они  выполняются,   то   процесс поиска   грубых   ошибок   можно   завершить.   В   противном   случае   следует опять  определить  номер  измерения  k, для которого абсолютное значение произведения |pV|   по результатам второго уравнивания   максимально.   Далее нужно составить систему из двух уравнений

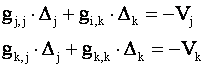                                           (2.9)

 

в которой поправки V_j, и V_k берутся из первого уравнивания сети. решают сис­тему и находят неизвестные , (повтор­но)  и .

Результаты j-го и k-го измерений ис­правляют поправками  и  и выпол­няют третье уравнивание сети; снова проверяют условия (2.8).

Если условия (2.8) выполняются, то про­цесс поиска грубых ошибок прекраща­ется; в противном случае опять опре­деляют номер измерения l с максималь­ным значением произведения |pV| и составляют систему уже из трех урав­нений, в которое подставляют поправки к измерениям из первого уравнивания сети.

Циклы уравнивания сети, определе­ния очередного номера измерения с максимальным значением произведения |pV|, составления и решения системы уравнений, проверки двух условий и исправления результатов измерений на величину вычисленных грубых ошибок теоретически можно выполнить (г - 1) раз, где г — число избыточных измере­ний в сети. На практике число грубых ошибок, как правило, не превышает одной трети от числа избыточных из­мерений, а число циклов уравнивания сети всегда на единицу больше числа обнаруженных грубых ошибок измере­ний.

Чтобы убедиться, что в геодезической сети обнаружены все грубые ошибки, необходимо составить контрольное уравнение

                    (2.10)

 

в которое нужно подставить последние значения вычисленных грубых ошибок и  сумму  поправок   из  первого  цикла уравнивания.

Расхождение левой и правой частей контрольного уравнения (2.10) при нор­мальном распределении остальных оши­бок измерений не должно превышать допуска, который можно рассчитать по формуле

                                     (2.11)

где г — число избыточных измерений;

n_гр — число обнаруженных грубых оши­бок;

 — средняя квадратическая ошиб­ка единицы веса до уравнивания