УДК 528.11

В.А. БОНДАРЕНКО, В.И. МИЦКЕВИЧ, Н.С. СЫРОВА (Белоруссия)

Уравнивание нивелирных сетей с поиском грубых ошибок измерений

Геодезия и картография. – 2003. - №5. – с. 26-28

 

Программа NIWА2, разработанная в Полоцком государственном университете для ПЭВМ, выпол­няет уравнивание и оценку точности нивелирных сетей параметрическим способом с поиском гру­бых ошибок в измерениях. Последнее осуществ­ляется по методике, которая основана на предложении, опубликованном в [3]. Нивелирная сеть уравнивается как свободная (опирающаяся на один исходный пункт)  с анализом отношения

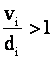                                                           (1)

где v_i – поправка в измерение из уравнивания, м;

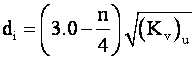                                       (2)

n — показатель степени (при n = 1,0 уравнивание выполняется по методу наименьших модулей; при n = 2,0 — по методу наименьших квадратов и т. д.). В подкоренном выражении используют­ся диагональные элементы матрицы

                                           (3)

в котором A — матрица коэффициентов парамет­рических уравнений  поправок;

Выражение (3) для корреляционной матрицы поправок справедливо в том случае, если диаго­нальные элементы матрицы весов измерении вы­числяют по  формуле

                                                (4)

где s_i — стандарт  измеренного  превышения, м.

За одно уравнивание исключается из обработки одно ошибочное измерение, для которого v_i/d_i, максимально, и одновременно выполняется неравенство (1).

В исходной информации к программе NIWА2 веса нивелирных линий могут задаваться по од­ной  из  четырех  формул:

где  L₀ — длина линии, км, для которой Р_i´ = 1; k₀ — число нивелирных  станций в линии.

Если нивелирная сеть многоклассная, то Р_i´ для превышений старшего класса умножают, а Р_i" делят на коэффициент а [4], определяемый по допускам инструкции. Например, при совме­стной обработке сетей нивелирования III и IV  классов

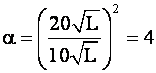
где   в скобках  даны  допуски   инструкции  на  ве­личину  свободных   членов условных  уравнений.

Программный переход от заданных Р_i" к Р_i´ осуществить легко. Для перехода от Р_i´ к Р_n предлагаем формулу

                                              (5)

где s₀ — стандарт измеренного превышения, мм, для которого L₀ или k₀ назначалось так, чтобы Р_i´ = 1. Как определить s₀ для одной любой ни­велирной линии, сказано в [4, с. 350]. В край­нем случае, можно s₀ назначить по h, указанной в табл. 1, с последующим применением выраже­ний s₀ = hÖ`L<sub>0</sub> или s<sub>0</sub> = hÖ`k₀. Но эта методика дает весьма приближенный результат для весов измерений.

Таблица 1

 

Применим программу NIWА2 для поиска гру­бых ошибок в измерениях для тестового примера из [1]. В табл. 2 указываются n — показатель степени; s₀ — погрешность линии 17 мм и но­мера линий в порядке выбора наибольшего и недопустимого v_i/d_i.

Таблица 2

 

По данным табл. 2 видно, что поиск ошибоч­ных превышений зависит от n и s₀. В табл. 3 приведены номера ошибочных линий не только при разных n, но и при разных s₀. Избранный тестовый пример удобен тем, что при n = 2,0 варианты исключаемых превышений зависят от начального номера превышения: 92 или 63, для которых v_i/d_i в начале счета практически оди­наково  и  недопустимо.

 

Сравнивая данные табл. 3 с результатами, опубликованными в [2],   можно сделать вывод, что найдены практически одни и те же ошибоч­ные линии. При этом нами в обработку взято превышение h_461-462 = 2,451 м для линии 64, указанное в [1]. Отметим, что в публикации [2] принято h_461-462 = 2,541 м для линии 64 и спра­ведливо утверждается, что оно содержит грубую ошибку.

СПИСОК ЛИТЕРАТУРЫ

1. Дьяков Б.Н., Рудикова М.П. О контроле, поиске и учете грубых ошибок измерений // Геодезия и картография. — 1997. — № 6. — С.  21—24.

2. Дьяков Б.Н., Рудикова М.П. Поиск гру­бых ошибок при обработке нивелирной сети // Геодезия и картография. — 1998. — № 8. — С.   13—14.

3. Коугия В.Л. Сравнение методов обнаруже­ния и идентификации ошибок измерений // Геодезия и картография. — 1998. — № 5. — С.  23—27.

4. Яковлев Н.В. Высшая геодезия. — М.: Нед­ра, 1989. — 445 с.