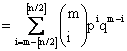Фрагмент статьи "Sign-constrained robust least squares, subjective breakdown point
|
3 Субъективная точка изломаПонятие точки излома впервые математически сформулировал Хемпел (1971,1974) как наиболее важное глобальное мероприятие робастности против грубых ошибок. Точка излома Хэмпела (1971) являеятся только асимптотической и не полностью свободна от распределения данных. Это может быть осложнить расчеты в некоторых случаях. В результате, Донохо и Хабер (1983) дальше значительно расширили понятие точки излома, приведя её к случаю конечной величины. С тех пор, как точка излома Донохо и Хабера (1983) действителна для конечной величины и не зависит от определенного распределения данных, оно широко используется как в теоретических, так и практических печатных изданиях по робастным статистикам. Известно, максимальная точка излома робастной процедуры составляет 0.5, за исключением двух случаев, которые не имеют никакой практической важности, как показали Донохо и Хабер (1983). Это может свидетельствовать о том, что никакая робастная процедура не смогла бы достичь значимых результатов для практической проблемы, если более чем 50% данных загрязнены грубыми ошибками. Общепринятый аргумент в поддержку этого это то, что никакие робастные методы не способны к выделению меньшинства хороших данных из большой части плохих данных. Должно ли это означать, что проблемы такого типа не имеют никакого практического и/или физического значения? Если бы мы рассуждали, как показано выше, наш ответ на этот вопрос несомненно утвердителен. В реальности, нам придется иметь дело с такими видами проблем. Например, мы знаем, что в определении тензоров напряжения от эпицентров землетрясения, одна из (двух) узловых плоскостей - (исправьте) замкнутая плоскость дефекта (хорошие данные), а другая - вспомогательная плоскость (плохие данные) (посмотрите например Ange-lier 2002;Xu 2004). Кроме того, некоторые из многих эпицентров землетрясения могут не являться результатом того же тензора напряжения, и их необходимо рассматривать как по настоящему ошибочные данные.
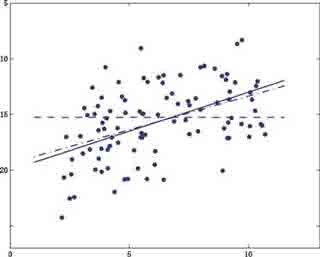
Рис. 1 Смоделированные данные примера, только за исключением промаха, который слишком велик, чтобы поместиться на этом рисунке. Также показано в этой фигуре - истинная линия регрессии (твердая линия), линия метода LMS, которая имеет излом из-за влияния промаха (пунктирная линия), и линия робастной оценки с условиями знаков, которая представлена дальше в параграфе 5 (пунктирная с точкой линия). Горизонтальные и вертикальные оси имеют значения xi и yi, соответственно. Другими словами, нам придется иметь дело с минимум 50% загрязнения данных в инверсии напряжения от эпицентров землетрясения. В обработке изображений, мы также выявили много шума среди сигнала. В этой статье мы будем предполагать, что мы имеем некоторую (не важно какую) предшествующую информацию о природе промахов или плохих данных. Включая предшествующую информацию внутри робастности, мы будем естественно развивать понятие субъективной точки излома, которая, возможно, была задумана как своего рода продолжение или реализация стохастического излома, предложенного Донохо и Хабером (1983). Эта новая точка излома может называться субъективной, если: (1) как она стала основываться на определенной предшествующей информации касающейся природы промахов; и (2) с тех пор, как такая предшествующая информация, может только отражать субъективное мнение аналитика данных о промахах. Мы покажем, что субъективная точка излома может действительно превысить известный максимум 0.5. Поэтому, понятие субъективной точки излома может обоснованно использоваться для того, чтобы решать проблемы, связанные физически более чем с 50% загрязнений. Для простоты рассуждений принимают в линейной модели Хотя величина приращения dyj может принимать любое большое число, мы принимаем, что значение dyi имеет распределение Бернулли, а именно:
- где Для удобства, но без потери общности, мы предполагаем, что значения остальных (m-i) dyj (j ≠ i) независимы и имеют те же распределения, как и dyi. Тогда общая вероятность распределения для значений промахов имеет биномиальное распределение:
(посмотрите например у Муда и др. (1974), где f(s) - вероятность s положительных dyi и (m- s) отрицательных dyj (j ≠ i). Хорошо известно, что, если m ≥ [n/2] +1, робастные процедуры будут иметь излом там, где [x] находится около целого, но меньше, чем x. Вопрос в том, какая вероятность того что робастная процедура будет иметь излом? Если робастный метод не применим почти точно или с большой вероятностью, мы не можем больше доверять и физически воспринимать результаты из набора зараженных данных. Наоборот, если робастный метод будет иметь излом с очень маленькой вероятностью, мы знаем, что он едва изламывается и мы будем доверять посчитанным результатам, полученных от зараженных данных или для интерпретации, или для практического использования. Очевидно, среднее арифметическое величин будет всегда искажено, если m ≥ 1, безразлично, имеем ли мы предшествующую информацию (4) или нет. Это нисколько не надёжно. В остальной части этой статьи мы сосредоточимся на величине медианы и α -усеченном среднем. Как для первого примера, давайте протестируем величину медианы. Хорошо известно, что медиана не искажается, если m ≤n/2 (для нечетных n) или m<n/2 (для четных). Таким образом мы сфокусируемся на том, чтоn/2+1≤ m ≤n. При заданных n, m, p, мы знаем, чтосубъективная точка излома медианы равна m/n (>0.5) и мы можем рассчитать вероятность для этой точки излома по формуле:
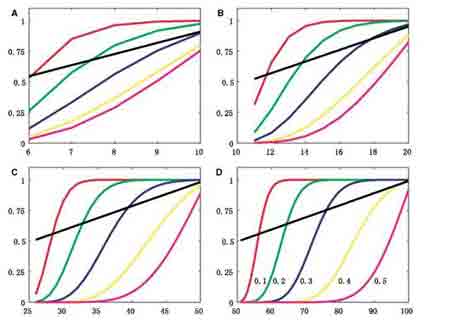
Рис.
2 Субъективные точки излома величины медианы и их соответствующие вероятности излома.
Горизонтальные и вертикальные оси показывают количество зараженных данных и
вероятность излома, соответственно. Шесть кривых в каждом подрисунке -
субъективные точки излома величины медианы (черная линия) и их соответственные
вероятности поломки с различными вероятностями для положительного значения
приращения yi (красная линия: p = 0.1; линия зеленая: p = 0.2; линия синяя: p =
0.3; желтая линия: p = 0.4; и пурпурно-красная линия: p = 0.5). Четыре подрисунка
А B, C и D соответствуют размерам образцов 11,21,51 и 101, соответственно.
Аналогично, мы можем также рассчитать вероятность того, что медиана не будет иметь излом по формуле:
В частности, если p = 1 (или q = 1) и если m≥ [n/2] + 1, тогда P(breakdown)= 1 или Pnot breakdown)= 0. В этом специальном случае, мы знаем, что медиана всегда имеет излом с вероятностью равной единице, и здесь нет смысла говорить о субъективной точке излома выше, чем 0.5. Другими словами, если p = 1 (или q = 1), медиана имеет максимальную точку излома 0.5. С другой стороны, если m≤ [n/2] , тогда мы всегда имеем P(излома)= 0 или P(не излома)= 1, что подтверждает общий смысл того, что медиана никогда не будет иметь излом, если загрязнение данных меньше 50%. Если p = q = 0.5, и допустим, что n = 101 и m = 55, тогда субъективная точка излома составляет 0.5446 и вероятность того, что медиана имеет излом составляет 2.0474X10-11 - почти ноль! Если количество загрязненных данных увеличивается до 75, субъективная точка излома составляет 0.7426 и соответствующая вероятность излома будет по прежнему также мала как и 0,0024442. Эти 2 примера несомненно продемонстрировали ,что имея априорную информацию, величина медианы может содержать в себе гораздо больше, чем 50% загрязненных данных с незначительной вероятностью излома. Чтобы, как положено увидеть как субъективная точка излома и соответствующая ей вероятность меняются в зависимости от m, p, n, мы выбрали p= 0,1, 0,2, 0,3, 0,4, 0,5 и n=11, 21, 51, 101 и показали результаты на рис.2. Очевидно, что вероятность субъективной точки излома стремительно возрастает с убыванием p от 0,5 до 0. Тем не менее она значительно уменьшается при увеличении количества величин n. В идеальном случае, если p=0,5 с увеличением величин медиана может содержать больший процент загрязнения без тревоги иметь излом. (сравните пурпурно-красные линии на рис.2). В подобном случае мы можем использовать для получения сведений о субъективной точке излома α -усеченное среднее и его соответствующую вероятность излома.
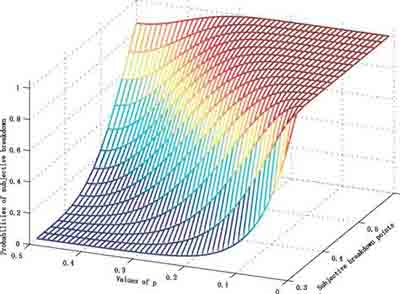
Рис. 3 Вероятности субъективных точек излома α -усеченного среднего с указанием субъективных точек излома и p. Здесь точка излома 0,3 (в смысле Хемпела). Две горизонтальные оси содержат субъективные точки излома и вероятности положительных значений δyi Как в случае с медианой, субъективная точка излома α -усеченного среднего может быть как большой, так и в смысле Hampel (1971) и/или Donoho и Huber (1983). В доказательство этому мы используем третий пример на Рис. 2, установив значение точки излома в смысле Hampel 0.3. Субъективные точки излома тогда будут между 0.3 и 0.6. С того момента, как число зараженных данных - не обязательно целое число, мы слегка уменьшаем количество величин с 51 до 50 так, что произведение 50 на 0.3 делает целое число. Вероятности субъективных точек излома показываются на Рис. 3. Очевидно на данном, что если p между 0.3 и 0.5, то α -усеченное среднее имеет хороший субъективную точку излома вплоть до 0.5, хотя оригинальная точка излома составляет только 0.3 (в смысле Hampel). Другими словами, α -усеченное среднее может содержать больше загрязнения в данных, если значения промахов имеют биномиальное распределение с p достаточно близкой к 0.5. Субъективные точки излома других робастных оценок и их соответсвующих вероятностей (субъективного) излома могут изучаться в подобной форме но будут пропущены в нашем случае. |