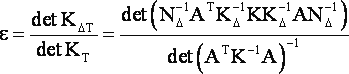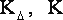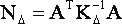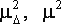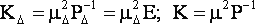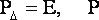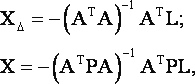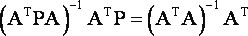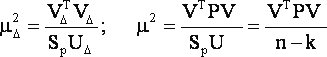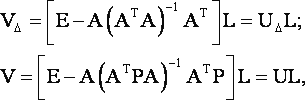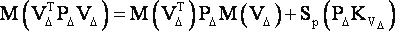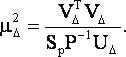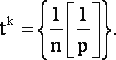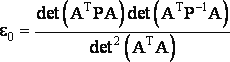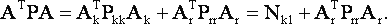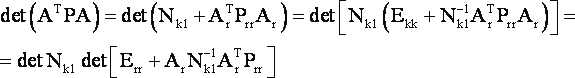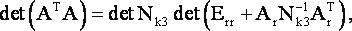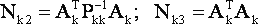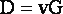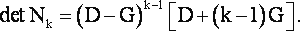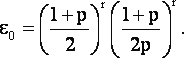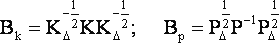УДК 528.118
Влияние ошибок весов измерений на результаты уравнивания и оценку точности
Автор В.И. Вершинин, "Геодезия и картография", 2000, №6, с. 17-22
Влияние весов измерений и их изменений на результаты уравнивания и апостериорную оценку точности относится к числу часто обсуждаемых проблем и поэтому составляет предмет исследований многих авторов [3, 5-8]. Это связано прежде всего с тем, что практически назначение весов измерений осуществляется не по теоретическим, а по эмпирическим дисперсиям и поэтому всегда является приближенным. Кроме того, получаемые таким образом значения весов оказываются смещенными [6]. В современных условиях проблема влияния изменений весов измерений приобретает особую значимость. Как известно, веса измерений непосредственно влияют на обусловленность систем нормальных уравнений и, следовательно, на точность результатов уравнивания. Весьма эффективный прием повышения этой точности - устойчивое, или регуляризованное, уравнивание, по существу, достигается за счет специального изменения весов измерений [3].
Изучение влияния ошибок весов измерений на результаты уравнивания и оценку точности всегда выполнялось или эмпирически, т.е. путем численных экспериментов на конкретных объектах [5, 7], или теоретически, т.е. путем получения аналитических выражений для оценки степени нарушения строгости уравнивания [2, 4, 8]. Однако как тот, так и другой путь непригодны для качественного анализа изучаемого явления, поскольку неизбежно связываются с конкретным объектом исследований и требуют большого объема вычислений для получения одного численного результата. Поэтому второй путь практически используется лишь для оценки влияния ошибок весов при обработке многократных измерений одной величины [2].
Нам не известны публикации в геодезической литературе, в которых были бы обоснованы простые формулы, удобные для априорного изучения влияния ошибок весов измерений на результаты уравнивания и оценку их точности. Поэтому целью настоящей статьи является попытка хоть частично восполнить указанный пробел.
В качестве основного показателя степени (коэффициента) нарушения строгости уравнивания будем вслед за [2, 4, 8] использовать значение, получаемое по формуле
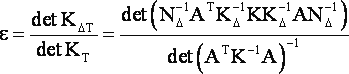 |
(1) |
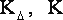 |
- приближенная и точная корреляционные матрицы измерений; |
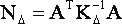 |
- матрица нормальных уравнений приближенного уравнивания. |
Для исследования влияния ошибок весов выражение (1) целесообразно представить в виде, в котором бы явно участвовали матрицы Q весовых коэффициентов, т.е.
 |
(2) |
где
 |
(3) |
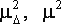 |
- приближенная и точная оценки дисперсии единицы веса; |
| k |
- число необходимых неизвестных. |
Наиболее распространенный практический прием формирования весовой матрицы в условиях, когда информация об относительной точности измерений отсутствует, сводится к принятию в качестве таковой единичной матрицы. В связи с этим примем
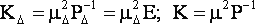 |
(4) |
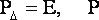 |
- приближенная и точная весовые матрицы измерений. |
Искомые решения в двух рассматриваемых схемах будут находиться по правилам
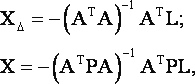 |
(5) |
а их различие
 |
(6) |
Из (6) следует, что искажения решений не произойдет только в том случае, если
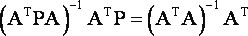 |
(7) |
Равенство (7) выполняется, например, когда весовые матрицы различаются лишь постоянным множителем или при математической обработке без избыточных измерений. В работе [4] указываются и другие виды весовых матриц, которые также не нарушают строгости уравнивания.
Сосредоточим основное внимание на исследовании искажений оценки точности. Как следует из (2), задача включает два этапа: 1) изучение изменения оценки µ 2 дисперсии единицы веса; 2) оценка относительного искажения величины определителя матрицы Q T весовых коэффициентов.
1) По результатам приближенного и строгого уравнивания определяют оценки
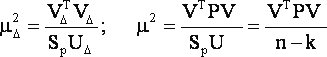 |
(8) |
где
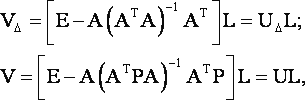 |
(9) |
| n |
- число всех измерений. |
Для сравнения устанавливаемых таким образом оценок найдем математическое ожидание. Используя известную зависимость, будем иметь
и, следовательно,
 |
(10) |
| Sp |
- символ следа матрицы. |
Заменяя теоретические параметры их оценками, на основании (10) получим
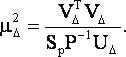 |
(11) |
Так как в большинстве случаев матрица Р является диагональной, то строгую формулу (11) можно заменить приближенной
и, следовательно,
 |
(12) |
 |
- сумма обратных весов измерений. |
Из (12) следует, что оценка дисперсии с приближенными весами смещена, и это смещение при Р > 1 всегда направлено в сторону завышения действительной точности.
На основании (12) для множителя из (2) будем иметь
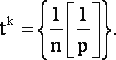 |
(13) |
2) Для оценки искажения величины определителя матрицы весовых коэффициентов представим коэффициент 0 из (3) в виде
или, учитывая свойства опаределителей,
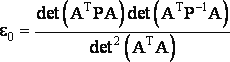 |
(14) |
Полученная формула позволяет совершенно строго оценивать степень искажения матрицы весовых коэффициентов уравненных неизвестных при использовании приближенных весов измерений.
На основании (14) несложно сделать важный вывод: при использовании лишь необходимых измерений любые ошибки в весах измерений не влияют на значение коэффициента 0, которое в этом случае строго равно 1. Аналогичный вывод обоснован иным путём в работе [4].
Последнее обстоятельство позволяет существенно упростить установление закономерности изменения величины определителя матрицы весовых коэффициентов вектора решений при изменении матрицы весов измерений. Учитывая эту особенность, точную весовую матрицу Р измерений зададим в виде
 |
(15) |
| r=n-k |
- число избыточных измерений; |
 |
- весовые матрицы необходимых и избыточных измерений. |
С учетом (15) выражение для матрицы нормальных уравнений точного решения принимает вид
Тогда
или
 |
(16) |
По аналогии будем иметь
 |
(17) |
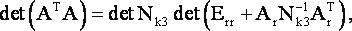 |
(17') |
где
Подставляя (16), (17) и (17') в выражение (14), получаем
 |
(18) |
Для дальнейшего упрощения выражения (18) воспользуемся предположением о следующей структуре матриц Nk [1]
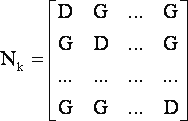 |
(19) |
Как отмечалось в [1], матрицы типа (19) примечательны тем, что, изменяя соотношение между их диагональными и недиагональными элементами
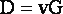 |
(20) |
(т.е. меняя значение v), можно в широком диапазоне изменять их обусловленность. Это обстоятельство приводит к тому, что результаты, получаемые с использованием таких матриц, не связываются с конкретной обусловленностью линейных систем.
Как известно, обратная матрица к матрице (19) имеет такое же строение (21):
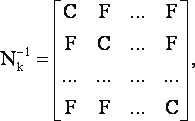 |
(21) |
где
 |
(22) |
а величина определителя матрицы Nk устанавливается по правилу
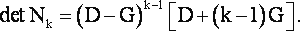 |
(23) |
Матрицам типа (19) соответствуют матрицы параметрических уравнений поправок вида [1]
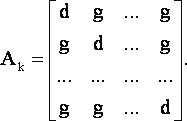 |
(24) |
Очевидно, что такую же структуру будет иметь и матрица Аr.
С использованием формул (19) - (24) выражение (18) преобразуется к виду
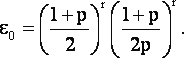 |
(25) |
Полученное выражение позволяет решать лишь часть поставленной задачи. В соответствии с (2), для получения конечного результата необходимое по (25) значение должно быть изменено множителем (13)
 |
(26) |
Таким образом, совокупность достаточно простых аналитических выражений (25) и (26) предоставляет удобный инструмент для априорного анализа характера изменения оценки точности результатов уравнивания в зависимости от ошибок весов измерений.
При отсутствии избыточных измерений (r = 0) на основании (25) получим известный результат и подтверждение его независимости от весов необходимых измерений.
Как следует из (2), показатель представляет собой отношение обобщенных дисперсий двух решений - с приближенным и точным знанием весов измерений. Однако для априорного анализа точности более удобным и наглядным был бы показатель, который отражает отношение обобщенных стандартов. Именно такой смысл будет иметь показатель, если его установить по формуле
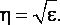 |
(27) |
Для иллюстрации возможностей полученных выражений при априорном анализе влияния ошибок весов на оценку точности результатов уравнивания проведем расчеты по формулам (2), (25), (26) и (27), варьируя значения р и r. Конкретизируем также некоторые условия. Во-первых, положим k = r, тогда на основании (26) получим
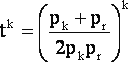 |
(28) |
Во-вторых, поскольку веса необходимых измерений не участвуют в формуле (25), то при расчетах используем Рkk = Е. В этом случае степень изменения весов измерений будет определяться лишь изменением весов избыточных измерений. Ограничимся разумным диапазоном изменения весов измерений (от 1,5 до 4) и числа избыточных измерений (от 1 до 20).
Результаты расчетов при принятых предположениях сведены в табл. 1.
Таблица 1
Веса измерений |
Показатели |
Число избыточных измерений r |
1 |
2 |
3 |
4 |
5 |
10 |
20 |
1.5 |
e0/e/n |
1.04/0.87/0.93 |
1.08/0.75/0.87 |
1.13/0.65/0.81 |
1.18/0.57/0.75 |
1.23/0.49/0.70 |
1.50/0.24/0.49 |
2.26/0.06/0.24 |
2.0 |
e0/e/n |
1.12/0.84/0.92 |
1.26/0.71/0.84 |
1.42/0.60/0.77 |
1.60/0.51/0.71 |
1.80/0.43/0.65 |
3.25/0.185/0.43 |
10.54/0.03/0.18 |
3.0 |
e0/e/n |
1.33/0.89/0.94 |
1.78/0.79/0.89 |
2.37/0.70/0.84 |
3.16/0.63/0.79 |
4.22/0.56/0.75 |
17.77/0.31/0.56 |
315.65/0.10/0.31 |
4.0 |
e0/e/n |
1.56/0.98/0.99 |
2.44/0.95/0.98 |
3.81/0.93/0.96 |
5.96/0.91/0.95 |
9.31/0.89/0.94 |
86.73/0.79/0.89 |
7521.52/0.62/0.79 |
Для более полной картины изучаемого явления приведем результаты ряда дополнительных расчетов. В табл. 1 помещены данные, соответствующие условиям, когда приближенные веса измерений меньше точных, а число избыточных измерений равно числу необходимых. Положим теперь р = 0,5 (приближенные веса больше точных). Тогда, например, при r = k = 5 получим
Сравнение полученного результата с числовыми данными соответствующей графы табл. 1 показывает, что в зависимости от соотношения приближенных и точных весов измерений происходит или завышение (n < 1) или занижение (n > 1) действительной точности.
Непосредственный практический интерес представляет характер искажений реальной точности при изменении соотношения числа необходимых и избыточных измерений. В табл. 2 помещены результаты расчетов при варьировании отношения r/k от 0,1 до 10. Не нарушая общности картины, при расчетах принято r = 10 и р =2.
Таблица 2
Показатели |
Отношение r/k |
0,10 |
0,25 |
0,33 |
0,50 |
1,00 |
2,00 |
3,00 |
5,00 |
10,00 |
е |
0,03 |
0,05 |
0,06 |
0,08 |
0,18 |
0,43 |
0,68 |
1,10 |
3,55 |
n |
0,18 |
0,22 |
0,24 |
0,29 |
0,43 |
0,66 |
0,82 |
1,05 |
1,88 |
Анализ результатов позволяет сделать следующие выводы, некоторые из них формулируются, по-видимому, впервые:
1. Степень искажения оценки точности не зависит от обусловленности матриц систем нормальных уравнений и целиком определяется соотношением числа необходимых и избыточных измерений и ошибками их весов;
2. При отсутствии избыточных измерений любые ошибки весов измеренных величин не нарушают строгости математической обработки;
3. При изменении соотношения числа необходимых и избыточных измерений и уровня ошибок их весов может происходить как завышение (n < 1), так и занижение (n > 1) реальной точности результатов уравнивания;
4. При некотором соотношении числа необходимых и избыточных измерений и уровня ошибок их весов искажения оценки точности не происходит (n = 1);
5. Максимальные искажения оценки точности могут значительно превышать тот уровень, который в геодезической литературе до сих пор считался предельным (20-25 % при 4-кратном изменении весов [4]).
В заключение отметим еще одно важное обстоятельство.
Известное в геодезической литературе [4, 8] неравенство
 |
(29) |
где a - отношение наибольшего и наименьшего собственных значений корреляционной матрицы В, обычно применяется для оценки как показателя e, так и e0, что некорректно.
Действительно, для первого и второго случаев соответственно будем иметь:
Равенство Вk = Вp. может выполняться лишь при условии, которое, как было показано выше, никогда не соблюдается. Поэтому, если неравенство (29) используется для оценки влияния ошибок весов [4, 8], то необходимо учитывать, что тем самым оценивается промежуточный e0, а не конечный e результат анализа.
Тогда при изменении действительных весов от 1 до р получим a = р и на основании (29), например при р = 2, будем иметь
Нетрудно заметить, что полученное (как и в [8]) значение верхней границы совпадает с данными табл. 1 при r = 1. Но это так и должно быть, поскольку выражение (25) при r = 1 можно представить в виде
 |
(30) |
Таким образом, сравнение выражений (29) и (30) показывает, что неравенство (29), часто используемое для оценки влияния ошибок весов измерений, позволяет находить лишь показатель e0 и всегда только при r = 1.
Литература:
1. Вершинин В.И. О методике исключения систематических ошибок измерений при уравнивании // Геодезия и картография. - 1986. - №12. - С. 10-14;
2. Дроздов Н.Д. Линейная алгебра в теории уравнивания измерений. - М.: Недра, 1972. - 214 с.;
3. Маркузе Ю.И. Рекуррентное и регуляризованное уравнивание как задача уравнивания с приближёнными весами измерений // Изв. вузов. Сер. Геодезия и аэрофотосъёмка. - 1988. - №6. - С. 3-15;
4. Маркузе Ю.И., Бойко Е.Г., Голубев В.В. Геодезия. Вычисление и уравнивание геодезических сетей. - М.: Картгеоцентр-Геодезиздат, 1994. - 431 с.;
5. Насретдинов К.К. Сравнение способов определения весов измерений из уравнивания // Геодещия и картография. - 1981. - №8. - С. 24-28;
6. Нейман Ю.М. О назначении весов по эмпирическим дисперсиям // Изв. вузов. Сер. Геодезия и аэрофотосъёмка. - 1968. - №3. - С. 26-31;
7. Овчинников В.А. Анализ чувствительности линейно-азимутальных сетей к назначению весовой матрицы // Изв. вузов. Сер. Геодезия и аэрофотосъёмка. - 1988. - №6. - С. 78-83;
8. Скейвалас И.М. Обобщённая оценка точности результатов уравнивания // Изв. вузов. Сер. Геодезия и аэрофотосъёмка. - 1984. - №52. - С. 13-17.