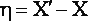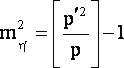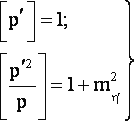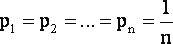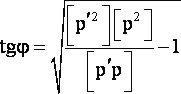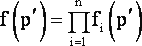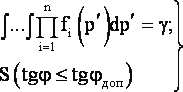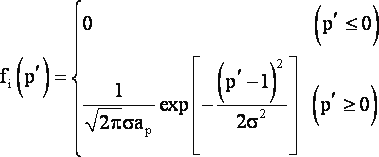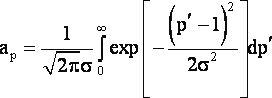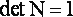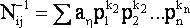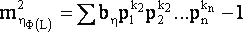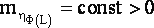Метод определения необходимой точности весов измерений
Автор С.Г. Могильный, "Инженерная геодезия", Республиканский межведомственный научно-технический сборник, 1972, вып. 12, с. 44-50
При внедрении в геодезическую и фотограмметрическую практику современных вычислительных машин возникает старый вопрос: стоит ли составлять громоздкие и сложные программы строгого уравновешивания измерений, если неизвестно точное значение соотношения весов. В опубликованных работах освещаются крайне противоречивые данные. Например, в работе [2] говорится, что колебание весов измерений в 2-2,5 раза можно не учитывать и принимать измерения равноточными, а в статье [4] утверждается, что веса нужно знать с точностью до 10-15%. Такое положение можно объяснить несовершенством методик исследования столь сложного вопроса.
В работах [2, 4] фактически не учтено, что не всякое изменение весов искажает результаты уравновешивания и что нельзя влияние ошибок весов оценивать так же, как и влияние ошибок измерений. Последнее замечание в большей степени касается работы [4]. Известен очевидный факт, что умножение всех весов на одно и то же число не изменит результатов уравновешивания. Возможно, что есть какие-то другие закономерности изменения весов, при которых искажений либо не будет, либо они окажутся незначительными. Следовательно, изменение абсолютных величин отдельных весов не может служить мерой их искажения, нужна какая-то более общая мера искажения всей совокупности весов уравновешиваемых измерений. Одна из возможных мер искажения совокупности весов может быть получена при рассмотрении общей арифметической середины.
Обозначим результаты независимых измерений через l1, l2, …, ln, точные значения весов измерений - р1, р2, …, рn; приближённые значения весов измерений через р'1, р'2, …, р'n. Всегда можно считать, что веса рi и p'i нормированы, т. е.
 |
(1) |
и
 |
(2) |
Можно считать доказанным [3, 5, 6], что за меру искажения результатов приближенного уравновешивания следует принимать mn - нормированное среднее квадратическое отклонение результатов строгого и приближенного уравновешивания. Если Х - общая арифметическая середина, вычисленная по весам рi, а Х' - по весам p'i, то разность
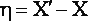 |
(3) |
показывает искажение результата конкретного уравновешивания. Для вычисления mn' необходимо найти среднее квадратическое значение величины n и разделить ее на среднюю квадратическую ошибку результата строгого уравновешивания. Опуская несложные преобразования и учитывая условия (1) и (2), получим
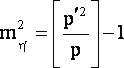 |
(4) |
Анализируя совместно условие (2) и формулу (4), можно увидеть, что существует бесконечное число совокупностей весов рi, которые приводят к одним и тем же искажениям результатов уравновешивания. Для выявления общего свойства таких совокупностей весов обратимся к геометрической интерпретации системы двух уравнений (2) и (4):
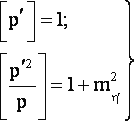 |
(5) |
Совокупность весов можно рассматривать как вектор в n-мерном пространстве, тогда система (5) является при mn² = const, уравнением эллипса в гиперплоскости n-мерного пространства. Для случая n = 3 сказанное выше изображено на рисунке.

Если измерения равноточны, то точные значения весов равны между собой:
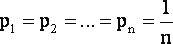 |
(6) |
Система (5) будет выражать уравнение окружности, лежащей в n-мерной гиперплоскости, и вектор точных весов будет перпендикулярен к плоскости этой окружности, поэтому система (5) будет иметь вид:
 |
(7) |
| ф |
- угол между вектором точных и приближённых весов |
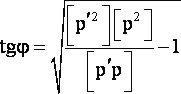 |
(8) |
Следовательно, искажение результата уравновешивания в этом случае однозначно определяется tgф, который следует принять за меру искажения совокупности весов.
Если точные значения весов неодинаковы, то определенному значению mn будет соответствовать некоторый интервал значений tgф, но середина этого интервала соответствует только одному значению mn, т. к. эллипсы (5) для разных mn' не пересекаются. Величина интервала значений tgф при mn' = const зависит от различия значений точных весов, но так как на практике не рекомендуется уравновешивать слишком неравноточные измерения, то интервал значений tgф довольно узок, так что можно считать, что и в случае неравных точных весах tgф между векторами весов определяет величину искажения mn', т. е.
 |
(9) |
Для определенного вектора точных весов функцию (9) легко вычислить, пользуясь уравнением (4). Зная (9), в каждом конкретном случае искажения весов можно оценить величины возможных отклонений результатов приближенного уравновешивания от строгого.
Однако для оценки необходимой точности задания весов измерений знание функции (9) недостаточно, так как оно не позволяет охватить в совокупности возможные искажения весов, если рассматривать их как случайные величины.
Пусть принимаемые для уравновешивания значения весов являются случайной выборкой из некоторой генеральной совокупности, имеющей функцию плотности вероятностей следующего вида:
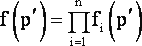 |
(10) |
В эту же генеральную совокупность входят значения точных весов. Если для конкретной задачи определить допустимую величину искажения mn(доп), то для заданного вектора точных весов можно определить tgфдоп.
Будем считать, что возможные случайные значения весов р'i достаточно близко располагаются возле точных значений весов рi, если вероятность отклонения вектора приближенных весов от точных весов на угол меньший фдоп - достаточно близка к 1 т. е.
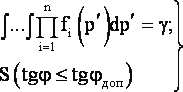 |
(11) |
Параметры распределения (10), удовлетворяющего условию (11), будут определять необходимую точность задания весов.
Чтобы оценить смысл полученных выводов, необходимо решить уравнение (11) для конкретного вида функции (10).
Для решения уравнения (11) предположим, что веса р' отдельных измерений являются независимыми случайными величинами со следующей функцией плотности вероятностей:
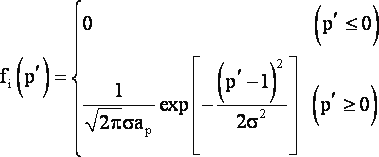 |
(12) |
где
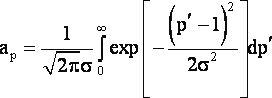 |
(13) |
Задавшись tgфдоп и у, при некотором п можно определить допустимую величину а² дисперсии весов (если а < 1, то с достаточной точностью можно принимать, что дисперсия и математическое ожидание веса р'i; равны соответственно а² и 1), при которой с вероятностью y искажение результата уравновешивания не превзойдет допустимого mn(доп). Прямое решение уравнения (14) - задача, практически невыполнимая уже при n > 3, поэтому для его решения использован метод статических испытаний, реализованный автором по составленной им программе на машине "Минск-22". В таблице представлены результаты вычислений вероятности у при указанных значениях tgфдоп и а для n = 2; 10; 100.
Значения вероятности у
а/tgфдоп |
n=2 |
n=10 |
n=100 |
0.20 |
0.50 |
0.80 |
0.20 |
0.50 |
0.80 |
0.20 |
0.50 |
0.80 |
0.20 |
0.81 |
0.46 |
0.34 |
0.63 |
0.00 |
0.00 |
0.56 |
0.00 |
0.00 |
0.60 |
1.00 |
0.89 |
0.80 |
1.00 |
0.89 |
0.67 |
1.00 |
1.00 |
0.79 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
1.00 |
Пользуясь данными таблицы, для принятых предположений о характере ошибок весов можно делать заключения следующего типа. Например, если для некоторой задачи допустимо искажение арифметической середины до mn'=0,6, что соответствует tgф = 0,6 и веса отдельных измерений колеблются случайным образом около 1 с а = 0,5 в формуле (12), то при числе измерений п = 100 практически достоверно можно утверждать, что искажение не превзойдет mn' = 0,6. Следовательно, в этих условиях веса со случайным разбросом около 1 с а = 0,5 можно принимать равноточными и утверждать что веса нужно определять с точностью, соответствующей а = 0,5.
Так как метод решения уравнения (14) не является точным, то следует иметь в виду, что значения вероятности у, указанные в таблице, могут содержать ошибку в пределах 5%. Имея для конкретного вектора строгих весов таблицу значений вероятности у, можно правильно решить вопрос о необходимой точности их определения. Для случая уравновешивания геодезической сети предположим, что
А - матрица коэффициентов уравнений погрешностей (п х г);
L - вектор-столбец истинных ошибок измерений (п измерений);
Р' - вектор приближенных весов (n-мерный);
Р - вектор точных весов (n-мерный).
Так как умножение весов на постоянное число не меняет результатов уравновешивания, то их всегда можно сделать такими, чтобы определитель матрицы N коэффициентов нормальных уравнений был равен 1:
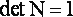 |
(15) |
Тогда каждый элемент обратной матрицы N -1 будет представлять собой полином степени (r - 1) следующего вида:
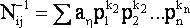 |
(16) |
| аn |
- постоянные коэффициенты, зависящие от формы сети |
В (16) суммирование ведется по всем целочисленным сочетаниям k1, k2, …, kn, которые удовлетворяют уравнению
 |
(17) |
считая нуль целым числом.
Если, учитывая условие (15), вычислить для произвольной функции Ф(L) измерений нормированную величину искажения из-за ошибок в весах, то она будет иметь вид, подобный (16):
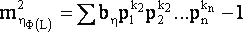 |
(18) |
| bn |
- постоянные коэффициенты, зависящие от формы сети и точных значений весов. |
В (18) суммирование ведется по всем целочисленным сочетаниям k1, k2, …, kn, удовлетворяющим уравнению
 |
(19) |
считая нуль целым числом.
Уравнение (15) имеет вид подобный (18), только сумма степеней значений весов р' должна быть равна r. Совместно уравнения (15) и (18) определяют некоторую кривую в пространстве n измерений, которую описывает вектор неточных весов р' , при водящий к одинаковым искажениям результатов в смысле величины.
Если приближенные веса равны строгим, поверхности (15) и (18) имеют только одну общую точку, соответствующую строгим значениям весов. Если
то поверхность (18) расширяется и пересекает поверхность (15) по некоторой замкнутой кривой, внутри которой находится точка, соответствующая строгим значениям весов. Следовательно, получается картина, аналогичная изображенной на рисунке и значит угол ф между векторами точных и приближенных весов может служить мерой искажения весов при уравновешивании сети. На основании изложенного выше предлагается следующая методика определения необходимой точности весов для уравновешивания геодезических сетей:
1. Пользуясь известными методами [3, 5, 6], для наиболее важных элементов сети вычисляется значение функций F (tgф) для нескольких определенных значений искажений весов. Число вычиляемых точек зависит от изменчивости функций F (tg ф) и необходимой точности интерполирования.
2. Определив по предыдущим вычислениям tgфдоп, из решения уравнения (11) определяются параметры распределения приближённых весов. Указанный путь решения практически легко реализуется с помощью ЭЦВМ типа "Минск-22".
Прямой путь решения задачи о необходимой точности весов приводит к решению уравнения типа (11) при удовлетворении переменными условий (15) и (18). Даже самой современной электронной машине потребуется очень много времени, чтобы справиться с такой задачей для простейших сетей. Следует ещё учесть необычайную сложность программы. Применение разработанной выше методики для конкретных сетей является предметом следующей статьи.
Литература:
1. Антонюженко В.Ф. О зависимости результатов уравновешивания от соотношения q. Сб. "Инженерная геодезия". Вып. 4. Киев, "Буддвелъник", 1968.
2. Визгин А.А. Анализ методов высокоточных угловых измерений и влияние ошибок в весах измеренных величин на результаты уравнивания геодезических построений". Сборник статей по геодезии. Вып. 12. М., Геодезиздат, 1962.
3. Визгин А.А. О принципах точности приближенных способов уравнивания. Труды Новосибирского института инженеров геодезии, аэрофотосъемки и картографии. Вып. 22, 1968.
4. Гордеев А.В. О точности весов измеренных величин, уравновешиваемых по способу посредственных измерений. Труды Московского института инженеров землеустройства. Вып. 19, 1963.
5. Могильный С.Г. Об оценке точности результатов уравнивания маркшейдерско-геодезических измерений. Известия вузов. "Горный журнал" 1965, № 1.
6. Никифоров Б.И. Рыхлюк Е.И. Оценка приближенных способов уравнивания. Труды Всесоюзного научно-исследовательского института горной геомеханики и маркшейдерского дела. Вып. 69, 1970.