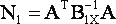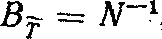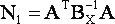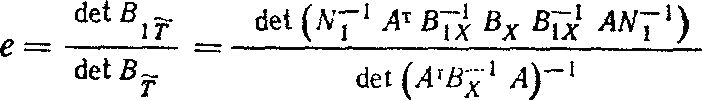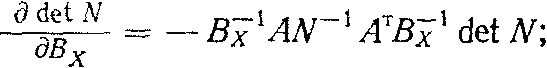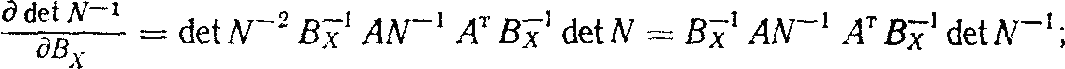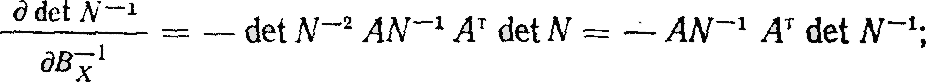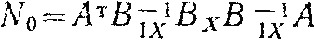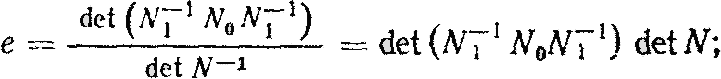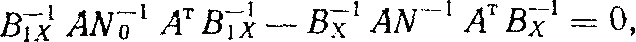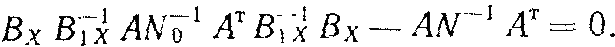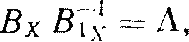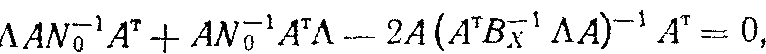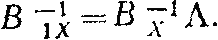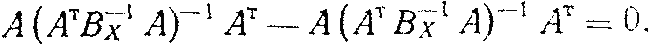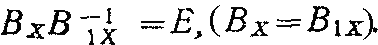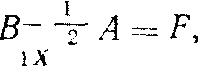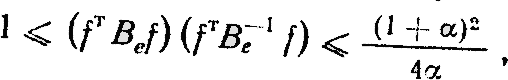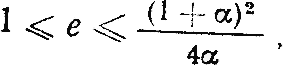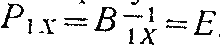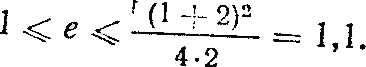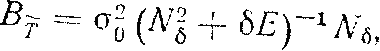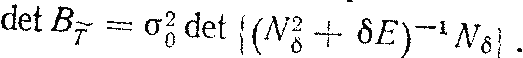УДК 528.1
Обобщённая оценка точности результатов уравнивания
Автор И.М. Скейвалас, "Известия вузов", серия "Геодезия и аэрофотосъёмка", 1984, №52, с. 13-17
Наряду с точечной и интервальной оценкой точности результатов уравнивания по методу наименьших квадратов в геодезии используются и обобщенные критерии точности. К ним относятся:
1) обобщенная дисперсия, т. е. det В;
2) среднее весовое от элементов корреляционной матрицы В, например Sp(FB);
3) спектральная норма (наибольшее собственное значение лmax) матрицы В.
Здесь применены обозначения: В - корреляционная матрица уравненных результатов измерений или параметров, Sp - символ следа матрицы, F - произвольная положительно определенная матрица.
Упомянутые критерии являются идентичными по выдаваемым результатам и показывают некоторую обобщенную точность всей геодезической сети в целом.
При дальнейших исследованиях будем использовать обобщенную дисперсию, т. е. det В.
Используя этот критерий, определим точность уравнивания геодезической сети, когда неизвестна истинная корреляционная матрица уравниваемых величин. Так, например, бывает когда игнорируется корреляция между уравниваемыми величинами или неточно известна матрица весов измеренных величин.
В случае уравнивания геодезической сети по методу наименьших квадратов с помощью параметров поправки к приближенным значениям параметров вычисляются по формуле:
 |
(1) |
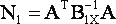 |
- матрица коэффициентов нормальных уравнений; |
| А |
- матрица коэффициентов уравнений поправок; |
| В1Х |
- корреляционная матрица уравниваемых (измеренных) величин (известна неточно); |
| L = AT - X |
- вектор-столбец свободных членов уравнений поправок; |
| Т |
- вектор-столбец приближенных значении параметров; |
| X |
- вектор-столбец результатов измерений (уравниваемых значений). |
Корреляционная матрица уравненных параметров Т вычисляется по формуле
 |
(2) |
так как BL = BX.
В случае равенства В1х = Вх определяем
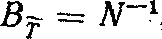 |
(3) |
где
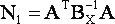
Установим относительную эффективность оценки по (1) как отношение ее обобщенной дисперсии к минимальной обобщенной дисперсии, т. е.
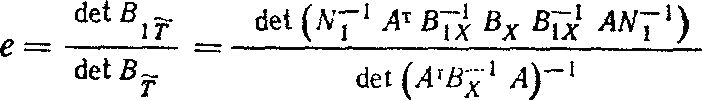 |
(4) |
При В1х = Вх получаем, что е = 1.
Определим интервал изменений относительной эффективности е, а также ее экстремумы.
Необходимые в дальнейшем частные производные по матрицам вычислим с использованием известных соотношений [1]:
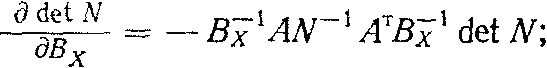 |
(5) |
 |
(6) |
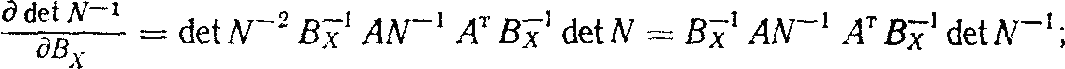 |
(7) |
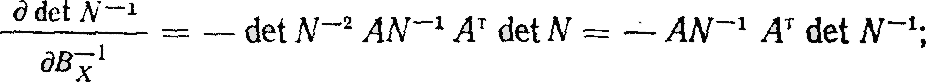 |
(8) |
 |
(9) |
где
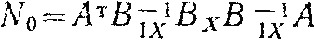
Используя выражения (5), (6), (7), (8), (9), напишем частные производные для е и определим экстремумы:
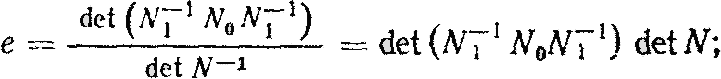 |
(10) |
и
 |
(11) |
в силу того, что det N1 <> 0, det N0 <> 0 и det N <> 0. Далее:
и
откуда
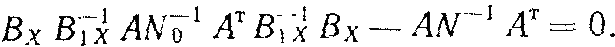 |
(12) |
Для решения выражения (12) зададимся условием
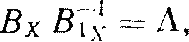 |
(13) |
где Л - матрица проектирования, т.е. Л² = Л, ЛT = Л, ЛА = А.
Выражение (11) с учетом (13) примет вид
где
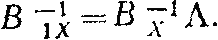
Далее:
Отсюда следует, что условие (13) является решением для выражения (11). Отдельный случай, когда
При условии (13) следует также, что е = 1. Решение (13) является минимумом, так как de/dB-11X меняет знак в окрестности этой точки.
Для решения уравнения (12) примем условие
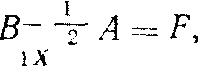 |
(14) |
где F - ортогональная матрица, т.е. FT = F-1, FFT = E.
При подстановке (14) в (12) имеем
откуда следует тождество ВХ - ВХ = 0.
Таким образом, условие (14) является решением выражения (12). Относительная эффективность е в этом случае выражается формулой
 |
(15) |
где
 |
(16) |
Для определения интервала изменений значений е воспользуемся известным неравенством Л.В. Канторовича [2].
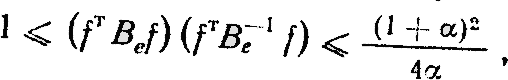 |
(17) |
| а = лmax/лmin; |
| л |
- символ собственного значения корреляционной матрицы Ве; |
| f |
- любой ортонормированный вектор-столбец; |
| Ве |
- корреляционная матрица (может быть любая положительно определенная эрмитова матрица). |
Всегда можно подобрать такой вектор f, чтобы выполнялось равенство
 |
(18) |
Таким образом, исходя из выражений (15), (17) и (18), следует, что е может принимать значения лишь в интервале
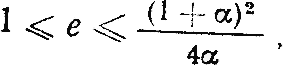 |
(19) |
| a |
- число обусловленности или число cond(Ве). |
Для примера определим относительную эффективность оценки Т или т, вычисленной по (1). Пусть веса результатов измерений принимаются равными между собой, т.е.
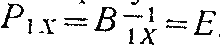
В самом деле веса их меняются до двух раз, т.е. от 1 до 2. Отсюда следует, что

Согласно (19) получаем относительную эффективность.
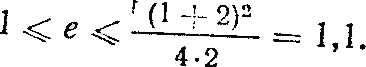
Таким образом, даже значительные ошибки весов имеют небольшое влияние на относительную эффективность при обобщенной оценке. Отсюда заключаем, что ошибки весов имеют незначительное влияние на дисперсии функций уравненных величин, так как обобщенная дисперсия является дисперсией некоторой функции.
Рассмотрим обобщенную оценку точности при регуляризованном уравнивании.
Корреляционная матрица уравненных параметров Т выражается [3]
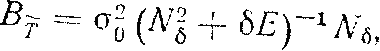 |
(20) |
| c0 |
-стандарт результата измерения с весом единица; |
| б |
- параметр регуляризации. |
Обобщенная дисперсия будет
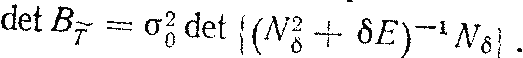 |
(21) |
Определим, при каких значениях б обобщенная дисперсия det Вт будет минимальна:
 |
(22) |
В силу невырожденности матрицы Nб получаем
 |
(23) |
и б определяем как результат решения уравнения (k-1)-го порядка. Таким образом, определение б не является однозначным. Заметим, что значение б = 0 не удовлетворяет (23). Следовательно, оценка по методу наименьших квадратов не является линейной оценкой с наименьшей обобщенной дисперсией.
Выводы
1. Обобщенная дисперсия представляет собой дисперсию некоторой функции уравненных величин, и по формуле (19) определяется относительная эффективность уравненных параметров
2. Ошибки весов имеют небольшое влияние на дисперсию функций уравненных величин.
3. Регуляризованное уравнивание дает оптимальную обобщенную дисперсию при нескольких значениях параметра регуляризации б. Оценка по методу наименьших квадратов не является линейной оценкой с наименьшей обобщенной дисперсией.
Литература
1. Бард Й. Нелинейное оценивание параметров. М.: Статистика, 1979, 352 с.
2. Канторович Л. В. Функциональный анализ и прикладная математика.- Успехи математических наук, 1948, №3 (28), с. 89-185.
3. О вариационном методе регуляризации при уравнивании свободных геодезических сетей /А.Н. Тихонов, В.Д. Большаков, В.А. Бывшев и др. - Изв. вузов. Геодезия и аэрофотосъемка, 1978, № 3, с. 3 -10.