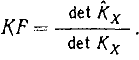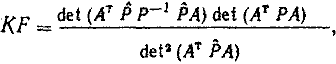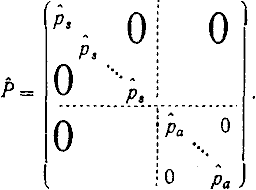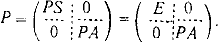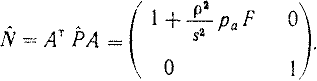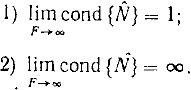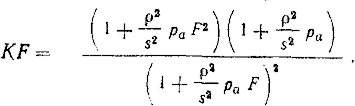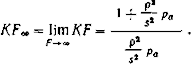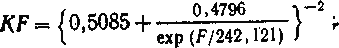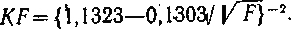Библиотека - Овчинников В.А. Анализ чувствительности линейно-азимутальных сетей к назначению весовой матрицы

УДК 528.118

Анализ чувствительности линейно-азимутальных сетей к назначению весовой матрицы

Автор В.А. Овчинников, "Известия вузов", серия "Геодезия и аэрофотосъёмка", 1988, №6, с. 78-83

     При уравнивании разнородных измерений существенным является вопрос назначения весов измерений. Фактически априорные значения веса измерения всегда имеют более или менее значительные отклонения от истинных значений. Кроме того, в общем случае истинная матрица измерений будет не диагональной.
     Представляет интерес вопрос оценки чувствительности линейно-азимутальных построений (сети трилатерации с дополнительно измеренными гироазимутами) к вариациям ковариационной матрицы измерений. В качестве меры такой чувствительности выберем коэффициент нарушения строгости уравнивания по методу наименьших квадратов [1].

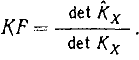          (1)

     Для анализа более удобно (1) представить в виде

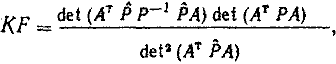          (2)

где А — матрица коэффициентов уравнений поправок; Р — истинная весовая матрица измерений; Р — фактически принимаемая при уравниваний весовая матрица.
     Матрица Р диагональная и имеет следующую структуру:

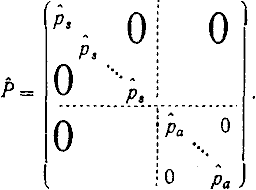          (3)

     Примем p_s = p_s= 1 и значение ра определим как

          (4)

     Структура матрицы Р имеет вид

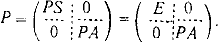          (5)

     Возьмем простейший вариант линейно-азимутального построения (рис. 1) и рассмотрим характер изменения обусловленности нормальной матрицы соnd{A^тРА} и коэффициента KF с изменением отношения F = p_a/p_a.
     Нормальная матрица будет иметь вид

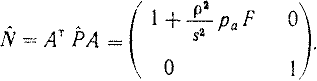          (6)

     Вид матрицы N позволяет сделать следующие выводы:

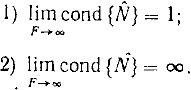          (7)

     Для определения значения KF найдем значения сомножителей, входящих в (2), и окончательно будем иметь

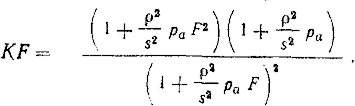          (8)

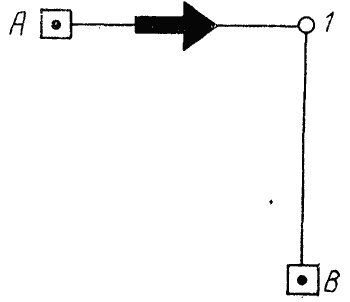Рисунок 1

     Выполним анализ полученного выражения:
     1) при F = t значение KF=1;
     2) при F —> 0

          (9)

     3) при F —>æ

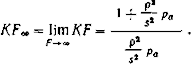          (10)

     Подставив характеристики построения (рис. 1) в (9) и (10), получим

          (11)

     Для анализа более сложных построений была составлена программа для ЭВМ ЕС 1045 на языке FORTRAN IV. Численные исследования были построены по схеме: каким будет KF, если вместо К принять К.
     Величина KF для заданного построения (координаты исходных и определяемых пунктов, информация о проектируемых измерениях, истинное значение веса азимута р_a) последовательно вычисляется при значениях коэффициента корреляции азимутов r_а равных 0,0; 0,3; 0,5; 0,8. Таким образом, при значениях r_а, отличных от 0,0, блок РА (5) является заполненным и определяется, исходя из следующего:

Рисунок 2

          (12)

где К_а — нормированная корреляционная матрица. При счете по программе вычисляется по 20 значений KF и соnd{N} для каждого из четырех значений r_а, при этом ра определяется для сочетаний m_s (см), равных 0,5; 2,0; 8,0; 32,0 и m"_а, равных 0,7; 2,1; 6,3; 18,9; 56,7.
     Результаты машинного счета для примера (рис. 1) представлены на графике (рис. 2). На графике сплошной линией показаны значения lnKF и прерывистой ln cond{N}. Как видно из рис. 2, эти результаты полностью согласуются с (7) и (11).
     В качестве примера приведем результаты, полученные для более сложного построения (рис. 3).

Рисунок 3

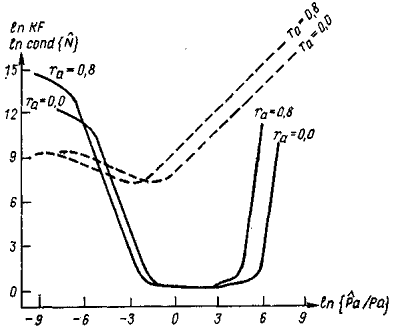Рисунок 4

     Вид графиков (рис. 4) имеет характерные особенности:
     1) график KF = f(F) асимметричен в точке F = 1, причем более пологая часть располагается в области F > 1;
     2) с ростом F (F > 1) значение cond{N} резко растет;
     3) при F < 1 рост cond{N} и KF ограничен сверху.
     Можно предположить, что правая часть (F > 1) графика KF = f(F) (рис. 4) должна иметь сходство с поведением KF на рис. 2, и расхождение в данном случае может быть объяснено неточностями численного решения, так как с ростом F задача становится все более плохо обусловленной. В этом случае вычисления необходимо проводить с двойной точностью, а также использовать метод регуляризации [2].
     Для практики наиболее интересен центральный участок графика W₀{KF Є {[1, 5]}. Для удобства анализа была выполнена аппроксимация результатов из W₀:

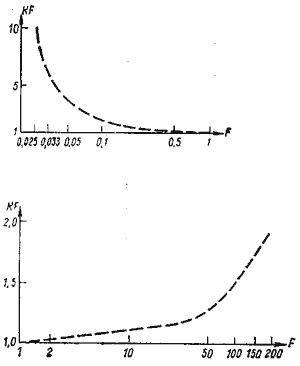Рисунок 5

для F > 1

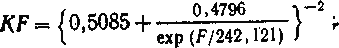          (13)

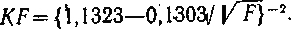          (14)

     В обоих случаях ошибка аппроксимации составила порядка 10%. Зависимости (13), (14) представлены на графиках (рис. 5).
     Для области W_o, отражающей интересы практики, сформулируем основные выводы:
     1) неучет коррелированности азимутов не отражается на KF;
     2) величина KF практически зависит лишь от F = p_a/p_a и может быть приближенно оценена по (13), (14);
     3) при уравнивании выгоднее несколько завышать р_а, однако обусловленность задачи в этом случае ухудшается.