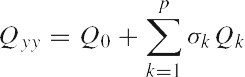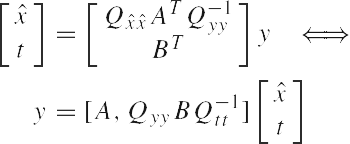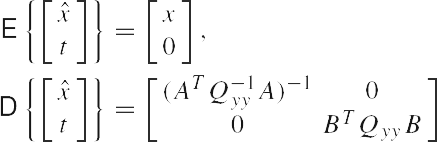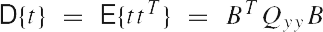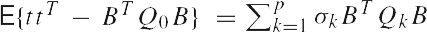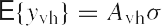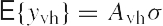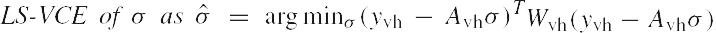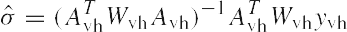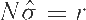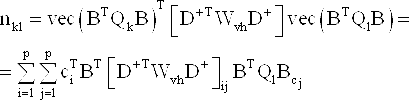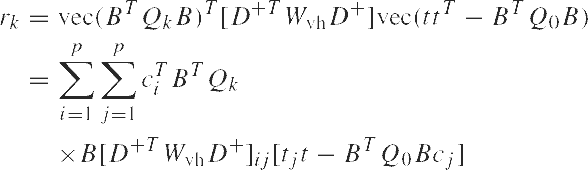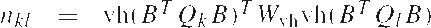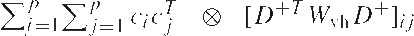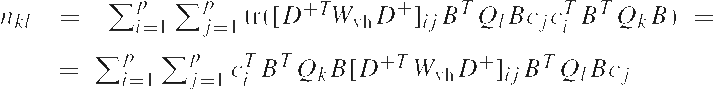Библиотека - P.J.G. Teunissen, A.R. Amiri-Simkooei. Оценка компонента дисперсии по методу наименьших квадратов

Оценка компонента дисперсии по методу наименьших квадратов

Авторы P.J.G. Teunissen, A. R. Amiri-Simkooei, "Journal of Geodesy", 2008, vol. 82, num. 2, p. 65-82, фрагмент, перевод статьи на русский язык выполнила Е.В. Захарова

Резюме. Оценка компонента дисперсии по методу наименьших квадратов (МНК-ОКД) - это простой, эластичный, приемлемый метод оценивания компонентов дисперсии и ковариаций. МНК-ОКД прост, поскольку он базируется на широкоизвестных принципах МНК; он эластичен, поскольку работает с задаваемой пользователем весовой матрицей; и он приемлем, т.к. позволяет полностью применять имеющиеся знания теории МНК. В этой статье мы представим МНК-ОКД для различных сценариев и исследуем их разнообразные свойства. Метод описывает три класса весовых матриц: общую весовую матрицу, весовую матрицу из класса единичных весовых матриц; и весовую матрицу, выведенную из класса эллиптического структурного распределения. Мы также сравним МНК-ОКД с другими существующими методиками. Некоторые из них являются частными случаями МНК-ОКД. Мы также покажем как, используя имеющиеся знания теории МНК, можно использовать одно из преимуществ изучаемых разных сторон, например такое, как точность ОКД, использование априорной информации о компоненте дисперсии, и проблема нелинейности ОКД. В заключение, мы покажем сходства и отличия между фиксированными результатами, оцененными по линейной модели и результатами, полученными с помощью МНК-ОКД. Приведём разнообразные примеры для иллюстрации теории.

2 Оценка компонентов ковариации по методу наименьших квадратов с учётом весов
2.1 Линейная модель ковариационного компонента

     Прежде всего, мы покажем некоторую формулировку линейной системы равенств неизвестных компонентов ковариации. Начнём с линейной модели

          (1)

где

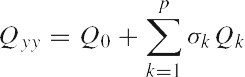          (2)

и где Е и D - операторы математического ожидания и дисперсии, соответственно.
      Модель (1) ограничивается двумя наборами неизвестных: вектор параметров х и ковариационные компоненты а_k, k = 1, . . . , p.
     Цель ОКД - создать оценщик неизвестных компонентов. Пусть известна размерность матрицы А - m¤n. Также пусть известно алгебраическое дополнение матрицы Q_k , k = 0, . . . , p и их взвешенная сумма

неотрицательно определена. Матрица Q₀ - известная часть матрицы дисперсий Q_yy.
     Теперь введём взаимно однозначное преобразование вектора наблюдений у, такое, чтобы выражения (1) приняли упрощённую форму. Пусть В - базисная матрица нулевого пространства A^T. Таким образом, В, размерностью m¤(m-n), - матрица, у которой линейные независимые столбцы охватывают нулевое пространство A^T:A^TB = 0 или B^TA = 0. Тогда существует следующее взаимно однозначное соответствие между у и (x^T, t^T):

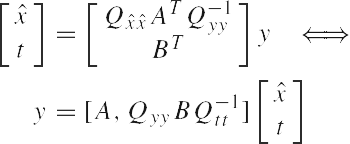          (3)

где

     Применяя это взаимно однозначное преобразование к выражению (1), мы получим линейную модель

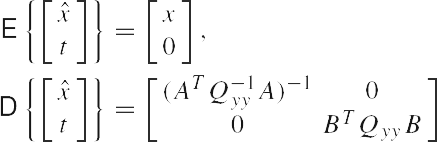          (4)

     Обратим внимание на нарушение связи между x и t. Мы признаём n-мерный вектор х наилучшей линейной несмещённой оценкой (НЛНО). Нулевое среднее (m-n)-мерного вектора t - избыточный вектор открытий. Он состоит из открытий, которые следуют из модели условных уравнений, B^TE{y} = 0. Избыточная линейная модель из выражений (1) определена как b = m - n. Вектор открытий t существует вследствие избыточности (b > 0). Два случайных вектора x и t некоррелированы. Они независимы, если у имеет нормальное распределение.
     Из уравнений (2) и (4) следует E{t} = 0 и

где

     Это уравнение может быть представлено в качестве матричного уравнения неизвестных ковариационных компонентов. Матричное уравнение состоит из b² скалярных уравнений . Мы можем привести матрицу наблюдений к привычной векторно-матричной форме, если скомпонируем вектор b, размерностью b¤1, с E{tt^T - B^TQ₀B} и получим вектор наблюдений размерностью b²¤1. Полученный вектор - так называемый, vec оператор.
     Тем не менее, поскольку матрица наблюдений tt^T - B^TQ₀B симметрична, мы будем рассматривать только диагональ матрицы наблюдений. Иначе будет происходить нежелательное удваивание данной величины. Это подразумевает, что мы будем использовать vh оператор вместо vec оператора (формулировка и свойства vec и vh операторов представлены в Приложении А). Использование vh оператора вместо vec оператора позволяет избежать проблем, связанных с вырожденной матрицей дисперсий. Матрица дисперсий vec(tt^T) - единичная, благодаря удваиванию, которое происходит на выходе tt^T. Используя vh оператор мы можем привести матрицу наблюдений к привычной векторно-матричной форме линейных уравнений

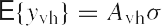          (5)

где

     Линейная модель (5) является фундаментальной основой нашей оценки ковариационных компонентов по методу наименьших квадратов. Вектор y_vh = vh(tt^T - B^TQ₀B), размерностью 1/2b(b + 1) играет роль вектора наблюдений. Таким образом, мы имеем 1/2b(b+1) уравнений и р неизвестных параметров а_k , k = 1, …, p. Примем, что планируемая матрица (5) имеет полный столбцевой ранг р. Избыточные измерения вышеуказанной модели в этом случае равны 1/2b(b + 1)-p.

2.2 Оценщик компонентов ковариации по методу наименьших квадратов с учётом весов

     Учитывая вышеуказанную линейную модель, мы можем прямо определить метод решения ковариационных компонентов по методу наименьших квадратов с учётом весов.
     Теорема 1 (МНК-ОКД с учётом весов).
     Пусть

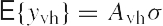          (6)

линейная модель ковариаций и нужно определить МНК-ОКД с учётом весов следующего выражения

где W_vh - весовая матрица. Тогда

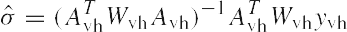          (7)

     Доказательство следует из стандартной теории метода наименьших квадратов.
     МНК-ОКД с учётом весов а имеет много полезных особенностей. Т.к. а - это алгоритм оценивания по методу наименьших квадратов, мы можем использовать прямые знания о теории метода наименьших квадратов. Эти опорные понятия верны для численных аспектов (из них может состоять стандартный пакет программ метода наименьших квадратов), так же как для многих статических.
     Сначала покажем, а позже будем использовать два различных возражения эквивалентных выражений для системы нормальных уравнений МНК-ОКД.
     Следствие 1 (нормальные уравнения МНК-ОКД)
     Пусть система нормальных уравнений МНК-ОКД (7) будет представлена как

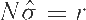          (8)

где нормальная матрица

и правая сторона

     Тогда n_kl получается на выходе нормальной матрицы N и r_k - на выходе вектора r:

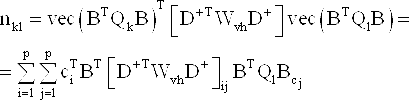          (9)

и

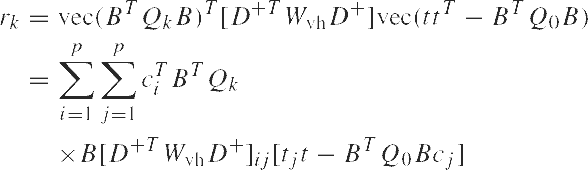          (10)

где D - удвоенная матрица, D⁺ - её псевдоинверсия, c_i - канонический единичный вектор, имеющий а на теоретическом выходе

(для формулы Кронекера и удвоенной матрицы зависимости с vec и vh операторами представлены в Приложении А).
     Доказательство для

и vh(.) = D⁺vec(.) в первой части обыкновенно. Можно переписать матрицу D^+TW_vhD⁺ размерностью b² ¤ b² в качестве суммы

где

имеет размерность b ¤ b. Сделаем замену этого выражения:

     Аналогично получается правая сторона r_k.

Вернуться в библиотеку