ДонНТУ |
Портал магистров ДонНТУ |
Назад
Источник:
В.А.Букринского Г.В.Орлова. «Сдвижение горных пород и земной поверхности при подземных разработках». М. Недра, 1984. 247с(48-51 стр.)
Расчеты деформаций земной поверхности при неизвестном расположении горных выработок
Для решения вопросов охраны сооружений от вредного влияния горных выработок
во многих случаях достаточно знать мак¬симальные деформации земной поверхности
Максимальные деформации развиваются в главных сечениях мульды вкрест
простирания, где возникают обычно несколько максимумов:
- два максимума - растягивающих горизонтальных деформаций;
- один или два максимума сжимающих горизонтальных деформаций;
- два максимума наклонов;
- два максимума кривизны выпуклости;
- один или два максимума кривизны вогнутости.
Для большинства сооружений наиболее опасными являются горизонтальные
деформации растяжения и кривизны выпуклости кривой оседания. Максимумы этих
деформаций возникают обычно на нижнем краю мульды сдвижения, т. е. на том краю,
который расположен над нижней границей очистных работ. Поэтому максимальные
деформации определяют на нижних краях мульд сдвижения.
Анализ данных натурных наблюдений позволяет заключить, что максимальные
деформации зависят от четырех основных факторов: мощности пласта, глубины горных
работ, угла падения и размеров выработки. Влияние последнего фактора можно не
принимать во внимание, если исходить только из условия полной подработки земной
поверхности.
Чтобы исключить влияние углов падения на первом этапе исследований, все
наблюдательные станции были разделены на две группы: с пологим и наклонным
падением (О-45°) и крутым падением (более 45°).
Поскольку выявление деформаций существенно зависит от длин интервалов между
реперами наблюдательных станций, для анализов отбирались только те станции, на
которых расстояние между реперами колебалось в пределах 10—20 м. Зависимости
максимальных деформаций от Н/т могут быть выражены равносторонними
гиперболами.
 (1)
(1)
где f max — максимальные деформации в общем виде, К=Н/т —
кратность.
Определение значения А для каждого вида деформаций произведено
следующим образом.
Из формулы (1) имеем А-Кf'тах. По этому выражению на каждой
наблюдательной станции и по каждому виду деформаций определялись коэффициенты
А. Затем выводились средние значения этих коэффициентов.
Таким путем были получены формулы для определения максимальных деформаций:
 (2)
(2)
где i'тах, &epsilonтах, Ктах — максимальные наклоны, растяжения
(сжатия) и кривизна.
Из формулы для максимальной кривизны определился минимальный радиус кривизны
 (3)
(3)
По формуле (3) определяют так называемые измеренные радиусы кривизны. Кроме
измеренных радиусов существуют расчетные радиусы, которые получают из сглаженных
расчетных кривых оседания.
Минимальный расчетный радиус кривизны можно выразить в зависимости от
отношения Н²/т.
Если в формулу R= L² / η таx × S″ (z)т подставить
L ≈ H; η тах =0,8т; S″ (z)т = 5, то получим:
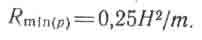 (4)
(4)
Здания и сооружения вписываются в свою кривую оседания, обусловленную
жесткостью зданий, которая не соответствует ни измеренной, ни расчетной кривой
оседания.
В первом приближении можно допустить, что сооружения вписываются в такую
кривую оседания, радиус кривизны которой определяется как среднегеометрический
радиус из расчетного и, измеренного радиусов кривизны:
 (5)
(5)
Для второго диапазона углов падения (а>45°) получены формулы максимальных
наклонов и растяжений в следующем виде:
 (6)
(6)
В целях повышения точности расчета использованы данные наблюдений по 64
наблюдательным станциям, охватывающим весь диапазон изменения углов падения от 0
до 64°. Для всех станций определяются коэффициенты А по максимальным
измеренным наклонам А1 и максимальным измеренным горизонтальным
деформациям А2.
По величине углов падения пласта станции разделены на 7 групп через каждые
10°. Если построить графики, на которых по оси абсцисс откладывать углы а, а по
оси ординат - средние значения коэффициентов А1 и А2, то, несмотря на некоторый
разброс, средние значения А1 и А2 располагаются в определенном порядке.
Наиболее вероятная зависимость А1 от углов а может быть выражена прямой
линией с уравнением А1 = 1600-17,5 a или, переходя к безразмерным относительным
величинам, А1 = 1,6-a/ρ.
Аналогичным образом зависимость коэффициента А2 от а может быть выражена
формулой:
А2 = (600+16 a) cos a или в безразмерных относительных единицах А2=
(0,6+0,9a/ρ) cos a, где ρ = 57° -радиан.
Полученные переменные коэффициенты значительно ближе к измеренным данным,
чем постоянные коэффициенты формул (2).
Вместо формул (2) можем записать:
 (7)
(7)
По новым формулам максимальные наклоны определяются с погрешностью ±35%,
максимальные горизонтальные деформа¬ции-с погрешностью ±50 %.
На основании анализа результатов наблюдений могут быть сделаны следующие
выводы:
1. Графики деформаций земной поверхности при больших глу¬бинах разработки
имеют более неравномерный характер, чем при средних глубинах.
При средних глубинах неравномерность наблюдается в основном на графиках
кривизны, при больших же глубинах она распространяется на графики наклонов и
горизонтальных деформаций. Однако с количественной стороны неравномерность в
распре¬делении деформаций при больших глубинах разработки существенного значения
не имеет, так как по абсолютной величине деформации весьма малы и можно
ограничиться определением только максимальных их величин.
2. При расчете сдвижений и деформаций земной поверхности от горных выработок
на больших глубинах (H>600 м) следует различать два возможных случая:
а) положение горных выработок в пластах в пространстве и времени известно
или задано календарными планами отработки пластов;
б) календарные планы отработки пластов отсутствуют и нет данных о размерах
выработок.
3. При известном положении горных выработок метод расчета деформации
выбирается в зависимости от отношения максимального оседания к глубине горных
работ ηmax/H. При ηmax /Н>1· 10 -³ расчет производится во всех точках мульды
сдвижения. При ηmax/H <1· 10-³ производится расчет только максимальных
величин деформаций. При этом максимальные деформации могут рассматриваться или
как некоторые функции f(m, Н,a), или как функции f(ηmax, Н).
Преимущество первого метода определения максимальных деформации состоит в
том, что все исходные влияющие факторы известны и прямо подставляются в формулы.
Во втором методе сначала определяют максимальное оседание (в этом трудность
и недостаток этого метода). Однако при больших глубинах этот метод может
оказаться более приемлемым, так как максимальное оседание само по себе отражает
влияние многих факторов. Для вывода зависимости второго типа был произведен
корреляционный их анализ.
На основании корреляционного анализа определялись зависимости второго типа
для максимальных наклонов imax = f1·(ηmax /H) и максимальных горизонтальных
деформаций εmax = f2·(ηmax /H)
По величине коэффициентов корреляции для максимальных наклонов r1 = 0,9; для
максимальных горизонтальных деформаций к2 =0,85. Можно считать, что связи между
imax и ηmax /Н, а также εmax и ηmax /Н линейные и достаточно надежные:
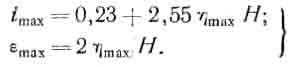 (8)
(8)
Сравнение измеренных деформаций с расчетными по формулам (7) и по формулам
(8) показало, что средние квадратические отклонения по первым формулам составили
40 %, по вторым 35%.
Следует считать эти погрешности вполне допустимыми, так как сами измеренные
деформации определяются также с погрешностью 20-23%.Таким образом, точность
расчета по обеим группам формул практически одинакова.
4. Когда календарные планы отсутствуют и нет возможности предусмотреть
размеры очистных выработок, расчет максималь¬ных деформаций производится по
формулам (6), (7).
Назад
 (1)
(1)  (2)
(2)  (3)
(3) 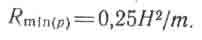 (4)
(4)  (5)
(5)  (6)
(6)  (7)
(7) 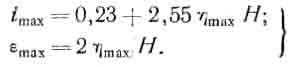 (8)
(8)