Abstract
In the paper an evolutionary approach for functional testing of digital circuits is considered. A genetic algorithm for testing digital multiplier is proposed. The main target of the proposed method is to generate as short as possible functional test wih as high as possible fault coverage with the goal to use the generated patterns as the input data for embedded functional BIST. Experimental data of the program realization is also represented.
1. Introduction
During the last thirty years of XX century, the ideas of evolution theory, self-organization and genetics developed for biological systems, were extended to the technical systems, hardware and software. The new direction in the theory and practice of artificial intelligence, called evolutionary computations, rapidly progresses now. The term evolutionary computations is applied to determination of the search, optimization or learning algorithms based on some formalized principles of natural evolutionary selection.
Evolutionary computations use various models of the evolutionary process, which are differed by diverse representations of solutions and genetic operators. This approach is successfully applied for digital circuits testing [1,2]. In the current paper the evolutionary approach to functional testing of digital circuits is considered.
Figure 1: Multiplier
Let us consider functional test generation for the combinational circuit of multiplier (Fig.1). Suppose that the operands X, Y and the result Z are integer numbers for simplicity (additional information about the multiplier circuit may be introduced). The task consists in functional test generation of the minimal length desirable. A genetic algorithm is applied for solving this problem.
2. Genetic algorithm for functional test generation
Genetic algorithms (GA) are one of the evolutionary computations paradigms. They are search algorithms based on the principles, which are similar to the natural selection principles [3]. GA use a random directional search to construct (sub)optimal solution of the given problem. A subset of points (which are potential problem solutions) is chosen from the search space. This subset is called a population in terms of the natural selection and genetics. Each potential solution of the problem – individual is presented by chromosome – some gene structure. An arbitrary gene of chromosome takes a value from some alphabet that encodes the points in the search space. In the simplest case, an individual can be represented by binary encoded string (for example 0011101). It makes the GA attractive for solving the problem of logic circuits test generation, where the solution is presented as a set of binary patterns or sequences of binary patterns. A fitness function is determined on the solution set. It allows to estimate the closeness of each individual to the optimal solution – the ability of survival. The genetic search of solution consists in the simulation of such artificial population evolution. Creation of new individuals during the population evolution is based on the reproduction process simulation. In this case the individuals-solutions involved in reproduction process are called the parents, contrary the obtained individuals-solutions are called the offsprings. In each generation a set of individuals-solutions is constructed using the parts of individuals-parents and adding new parts with “good properties”. Thus the GA effectively uses the information accumulated during evolution process.
For solving any problem with genetic algorithm, first of all, we have to define: 1) the form of individual representation – encoding; 2) genetic operators – crossover and mutation; 3) fitness function (Fig.2). Further we shall consider all these factors with reference to the given problem.
Figure 2
In the following we will consider the definition of all GA components with the reference to the formulated problem.
1) A single test pattern consists of two integer numbers X and Y – the operands of multiplier. Therefore a decision is represented as two-component vector (X,Y). On the other hand, we will use binary strings – codes of the numerical vectors, as decision representation.
2) Two types of genetic operators (crossover and mutation) are used – arithmetical and binary.
In accordance with arithmetical crossover
for two parents 
and
, a new
individual-offspring 
is
defined as follows
,
,
where 
.
Since we consider integer operands of multiplier and
the described numerical crossover can generate real numbers, then we have to
round off the generated components of the vector 
.
Binary crossover is executed according to the classical scheme represented below in Fig. 3
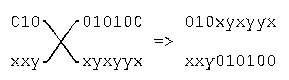
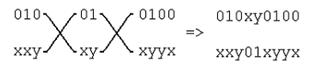
Figure 3: One-point and two-point binary crossover operators
At the same time each type of crossover is
applied with its own probability 
(binary) and 
(numerical): 
. Note, that both types of crossover are
used as it is shown in the algorithm pseudocode (Fig.5).
For mutation operators we also use
two types – arithmetical and binary mutation. Arithmetical
mutation for functional testing is implemented as follows. New individual 
-«mutant» is obtained from old individual according to
expressions
,
where 
- is small number. Obtained individual A’
must be rounded off also.
Binary mutation is implemented in accordance with the traditional method (Fig.4)
01001011 ® 01000011
Figure 4: Binary mutation
At the same time each type of mutation is
applied with its own probability 
(binary) and 
(numerical): 
.
3) At the preliminary stage the test pattern quality is evaluated in the following way. The number of inverted bits in the multiplication result is estimated for each bit inversion in the current test pattern. The experiments have shown that a test pattern, where any bit inversion will lead to at least one bit inversion in the multiplication result, can be always found.
Our goal is now to generate test patterns such that
the bit inversions of input operands produce maximum bit inversions in the
multiplication result (it would be desirable to have all bit inversions). Thus
we can define the matrix P of dimension 
, where 
, if i-th
input bit inversion produces j-th output bit inversion. The matrix P is defined in the following way. First, all the matrix
cells are zeros. Next, in the selected input pattern every bit is inverted. The
matrix cells 
are
defined in accordance to the produced bit inversions in the output pattern. The
fitness function is defined as
.
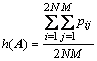Further the genetic algorithm of functional test generation is considered, its pseudocode is represented in Fig. 5. The test generation of single patterns is executed in AddBestInputToTest()function. After the next iteration of new population generation an input test sequence is changed. If appending the best individual of the population leads to increasing test sequence fitness-function, then it is included to test.
The main target of the proposed method is to generate as short as possible functional test wih as high as possible fault coverage with the goal to use the generated patterns as the input data for embedded functional BIST [5]. The final fault coverage of the BIST can be increased to 100% by improving the controllability and observability of the circuit.
and 
, coefficients 
and 
for functional
crossingover and mutation accordingly, the individuals number in population –
100. Under these conditions the dependence of test fitness-function (fault
coverage) from generations number was investigated. The experimental data in
Fig. 6 show that fitness-function value is stabilized enough quickly. Hence the
boundary value of GA generations number is chosen equal to 40.
