7. Genetic Algorithms
Автор: John H. Holland
Издательство: First MIT Press
ISBN-10: 0-262-58111-6
ISBN-13: 978-0-262-58111-0
Год: 1998
Источник : First MIT Press
Описание: Computer programs that "evolve" in ways that resemble natural selection can solve complex problems even their creators do not fully understand.




Genetic Algorithms
Computer programs that "evolve" in ways that resemble natural selection can solve complex problems even their creators do not fully understand
by John H. Holland

Living organisms are consummate problem solvers. They exhibit a versatility that puts the best computer programs to shame. This observation is especially galling for computer scientists, who may spend months or years of intellectual effort on an algorithm, whereas organisms come by their abilities through the apparently undirected mechanism of evolution and natural selection.

Pragmatic researchers see evolution's remarkable power as something to be emulated rather than envied. Natural selection eliminates one of the greatest hurdles in software design: specifying in advance all the features of a problem and the actions a program should take to deal with them. By harnessing the mechanisms of evolution, researchers may be able to "breed" programs that solve problems even when no person can fully understand their structure. Indeed, these so-called genetic algorithms have already demonstrated the ability to made breakthroughs in the design of such complex systems as jet engines.

Genetic algorithms make it possible to explore a far greater range of potential solutions to a problem than do conventional programs. Furthermore, as researchers probe the natural selection of programs under controlled an well-understood conditions, the practical results they achieve may yield some insight into the details of how life and intelligence evolve in the natural world.

Most organisms evolve by means of two primary processes: natural selection and sexual reproduction. The first determines which members of population survive and reproduce, and the second ensures mixing and recombination among the genes of their offspring. When sperm and ova fuse, matching chromosomes line up with one another and then cross-over partway along their length, thus swapping genetic material. This mixing allows creatures to evolve much more rapidly than they would if each offspring simply contained a copy of the genes of a single parent, modified occasionally by mutation. (Although unicellular organisms do not engage in mating as humans like to think of it, they do exchange genetic material, and their evolution can be described in analogous terms.)

Selection is simple: if an organism fails some test of fitness, such as recognizing a predator and fleeing, it dies. Similarly, computer scientists have little trouble weeding out poorly performing algorithms. If a program is supposed to sort numbers in ascending order, for example, one need merely check whether each entry of the program's output is larger than the preceding one.

People have employed a combination of crossbreeding and selection for millennia to breed better crops, racehorses or ornamental roses. It is not as easy, however, to translate these procedures for use on computer programs. The chief problem is the construction of a "genetic code" that can represent the structure of different programs, just as DNA represents the structure of a person or a mouse. Mating or mutating the text of a FORTRAN program, for example, would in most cases note produce a better or worse FORTRAN program but rather no program at all.

The first attempts to mesh computer science and evolution, in the late 1950's and early 1960's, fared poorly because they followed the emphasis in biological texts of the time and relied on mutation rather than mating to generate new gene combinations. Then in the early 1960s, Hans J. Bremermann of the University y of California at Berkeley added a kind of mating: the characteristics of offspring were determined by summing up corresponding genes in two parents. This mating procedure was limited, however, because it could apply only to characteristics that could be added together in a meaningful way.

During this time, I had been investigation mathematical analyses of adaptation and had become convinced that the recombination of groups of genes by means of mating was a critical part of evolution. By the mid-1960's I had developed a programming technique, the genetic algorithm, that is well suited to evolution by both mating and mutation. During the next decade, I worked to extend the scope of genetic algorithms by creating a genetic code that could represent the structure of any computer program.

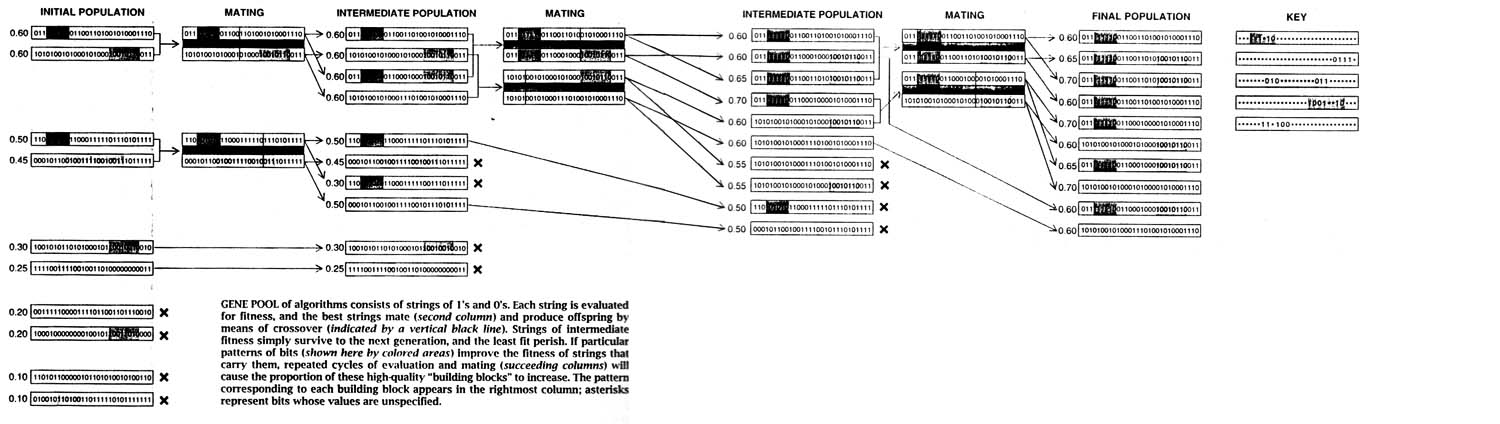
The result was the classifier system, consisting of a set of rules, each of which performs particular actions every time its conditions are satisfied by some piece of information. The conditions and actions are represented by strings of bits corresponding to the presence or absence of specific characteristics in the rules' input and output. For each characteristic that was present, the string would contain a 1 in the appropriate position, and for each that was absent, it would contain a 0. For example, a classifier rule that recognized dogs might be encoded as a string containing 1's for the bits corresponding to "hairy," "slobbers," "barks," "loyal" and "chases sticks" and 0's for the bits corresponding to "metallic," "speaks Urdu" and "possesses credit cards." More realistically , the programmer should choose the simplest, most primitive characteristics so that they can be combined as in the game of 20 Questions.to classify a wide range of objects and situations.

Although they excel at recognition, these rules can also be made to trigger actions by tying bits in their output to the appropriate behavior [ see illustration on page 69]. Any program that can be written in a standard programming language such as FORTRAN of LISP can be rewritten as a classifier system.

To evolve classifier rules that solve a particular problem, one simple starts with a population of random strings of 1's and 0's and rates each string according to the quality of the result. Depending on the problem, the measure of fitness could be business profitability, game payoff, error rate or any number of other criteria. High-quality strings mate; low-quality ones perish. As generations pass, strings associated with improved solutions will predominate. Furthermore, the mating process continually combines these strings in new ways, generating ever more sophisticated solutions. The kinds of problems that have yielded to the technique range from developing novel strategies in game theory to designing complex mechanical systems.

Recast in the language of genetic algorithms, the search for a good solution to a problem is a search for particular binary strings. The universe of all possible strings can be considered as an imaginary landscape; valleys mark the location of strings that encode poor solutions, and the landscape's highest point corresponds to the best possible string.

Regions in the solution space can also be defined by looking at strings that have 1's and 0's in specified places, a kind of binary equivalent of map coordinates. The set of all strings that start with a 1, for example, constitutes a region in the set of possibilities. So do all the strings that start with a 0 or that have a 1 in the fourth position, a 0 in the fifth and 1 in the sixth and so on.

One conventional technique for exploring such a landscape is hill climbing: start at some random point, and if a slight modification improves the quality of your solution, continue in that direction; otherwise, fo in the opposite direction. Complex problems, however, make landscapes with many high points. As the number of dimensions of the problem space increases the countryside may contain tunnels, bridges and even more convoluted topological features. Finding the right child or even determining which way is up becomes increasingly difficult. In addition, such search spaces are usually enormous. If each move in aches game, for example, has an average of 10 alternatives, and a typical game lasts for 30 moves on each side, then there are about 1060 strategies for playing chess (most of them bad).

Genetic algorithms cast a net over this landscape. The multitude of strings in an evolving population samples it in many regions simultaneously. Notably, the rate at which the genetic algorithm samples different regions corresponds directly to the regions' average "elevation" - that is, the probability of finding a good solution in that vicinity.

This remarkable ability of genetic algorithms to focus their attention on the most promising parts of a solution space is a direct outcome of their ability to combine strings containing partial solutions. First, each string in the population is evaluated to determine the performance of the strategy that is encodes. Second, the higher-ranking strings mate. Two strings line up, a point along the strings is selected at random and the portions to the left of that point are exchanged to produce two offspring: one containing the symbols of the first string up to the crossover point and those of the second beyond it, and the other containing the complementary cross. Biological chromosomes cross over one another when two gametes meet to form a zygote, and so the process of crossover in genetic algorithms does in fact closely mimic its biological model. The offspring do not replace the parent strings; instead they replace low-fitness strings, which are discarded at each generation so that the total population remains the same size.

Third, mutations modify a small fraction of the strings: roughly one in every 10,000 symbols flips from 0 to 1, or vice versa. Mutation alone does not generally advance the search for a solution, but it does provide insurance against the development of a uniform population incapable of further evolution.

The genetic algorithm exploits the higher-payoff, or "target," regions of the solution space, because successive generations of reproduction and crossover produce increasing numbers of strings in those regions. The algorithm favors the fittest strings as parents, and so above-average strings (which fall in target regions) will have more offspring in the next generation.

Indeed, the number of strings in a given region increases at a rate proportional to the statistical estimate of that region's fitness. A statistician would need to evaluate dozens of samples from thousands or millions of regions to estimate the average fitness of each region. The genetic algorithm manages to achieve the same result with far fewer strings and virtually no computation.

The key to this rather surprising behavior is the fact that a single string belongs to all the regions in which any of its bits appear. For example, the string 11011001 is a member of regions 11****** (where the * indicates that a bit's value is unspecified), 1******1, **0**00* and so forth. The largest regions-those containing many unspecified bits-will typically be sampled by a large fraction of all the strings in a population. Thus, a genetic algorithm that manipulates a population of a few thousand strings actually samples a vastly larger number of regions. This implicit parallelism gives the genetic algorithm its central advantage over other problem-solving processes.

Crossover complicates the effects of implicit parallelism. The purpose of crossing strings in the genetic algorithm is to test new parts of target regions rather than testing the same string over and over again in successive generations. But the process can also "move" an offspring out of one region into another, causing the sampling rate of different regions to depart from a strict proportionality to average fitness. That departure will slow the rate of evolution.

The probability that the offspring of two strings will leave its parents' region depends on the distance between the 1's and 0's that define the region. the offspring of a string that samples 10****, for example, can be outside that region only if crossover begins at the second position in the string-one chance in five for a string containing six genes. (The same building block would run a risk of only one in 999 if contained in a 1,000-gene string.) The offspring of a six-gene string that samples region 1****1 runs the risk of leaving its parents' region no matter where crossover occurs.

Closely adjacent 1's or 0's that define a region are called compact building blocks. They are most likely to survive crossover intact and so be propagated into future generations at a rate proportional to the average fitness of strings that carry them. Although a reproduction mechanism that includes crossover does not manage to sample all regions at a rate proportional to their fitness, it does succeed in doing so for all regions defined by compact building blocks. The number of compactly defined building blocks in a population of strings still vastly exceeds the number of strings, and so the genetic algorithm still exhibits implicit parallelism.

Curiously, an operation in natural genetics called inversion occasionally rearranges genes so that those far apart in the parents may be placed close to one another in the offspring. This amounts to redefining a building block so that it is more compact and less subject to being broken up by crossover. If the building block specifies a region of high average fitness, then the more compact version automatically displaces the less compact one because it loses few offspring to copying error. As a result, an adaptive system using inversion can discover and favor compact versions of useful building blocks.

The genetic algorithm's implicit parallelism allows it to test and exploit large numbers of regions in the search space while manipulating relatively few strings. Implicit parallelism also helps genetic algorithms to cope with nonlinear problems - those in which the fitness of a string containing two particular building blocks may be much greater (or much smaller) than the sum of the fitnesses attributable to each building block alone.

Linear problems present a reduced search space because the presence of a 1 or a 0 at one position in a string has no effect on the fitness attributable to the presence of a 1 or 0 somewhere else. The space of 1,000-digit strings, for example, contains more than 31000 possibilities, but if the problem is linear, an algorithm need investigate only strings containing 1 or 0 at each position, a total of just 2,000 possibilities.

When the problem is nonlinear, the difficulty increases sharply. The average fitness of strings in the region *01**, for example, could be above the population average, even though the fitnesses associated with *0*** and **1*** are below the population average. Nonlinearity does not mean that no useful building blocks consisting of single 1's or 0's will be inadequate. That characteristic, in turn, leads to an explosion of possibilities: the set of all strings 20 bits in length contains more than three billion building blocks. Fortunately, implicit parallelism can still be exploited. In a population of a few thousand strings, many compact building blocks will appear in 100 strings or more, enough to provide a good statistical sample. Building blocks that exploit nonlinearities to attain above-average performance will automatically be used more often in future generations.

In addition to coping with nonlinearity, the genetic algorithm helps to solve a conundrum that has long bedeviled conventional problem-solving methods: striking a balance between exploration and exploitation. Once one finds a good strategy for playing chess, for example, it is possible to concentrate on exploiting that strategy. But his choice carries a hidden cost because exploitation makes the discovery of truly novel strategies unlikely. Improvements come from tying new, risky things. Because many of the risks fail, exploration involves a degradation to what degree the present should be mortgaged for the future is a classic problem for all systems that adapt and learn.

The genetic algorithm's approach to the obstacle turns on crossover. Although crossover can interfere with the exploitation of a building block by breaking it up, the process of recombination tests building blocks in new combinations and new contexts. Crossover generates new samples of above-average regions, confirming or disapproving the estimates produced by earlier samples. Furthermore, when crossover breaks up a building block, it produces a new block that enables the genetic algorithm to test regions it has not previously sampled.

The game known as the Prisoner's Dilemma illustrates the genetic algorithm's ability to balance exploration against exploitation. This long-studied game presents its two players with a choice between "cooperation" and "defection": if both players cooperate, they both receive a payoff; if one player defects, the defector receives a higher payoff and the cooperator receives nothing; if both defect, they both receive a minimal payoff [ see table on page 71 ]. For example, if player A cooperates and player B defects, then player A receives no payoff and player B receives a payoff of five points.

Political scientists and sociologists have studied the Prisoner's Dilemma because it provides a simple, clear-cut example of the difficulties of cooperation. Game theory predicts that each player should minimize the maximum damage the other player can inflict: that is, both players should defect. Yet when two people play the game together repeatedly, they typically learn to cooperate with each other to raise their joint payoff. One of the most effective known strategies for the Prisoner's Dilemma is "tit for tat," which begins by cooperating but thereafter mimics the last play of the other player. That is, it "punishes" a defection by defecting the next time, it rewards cooperation by cooperating the next time.



Robert Axlerod of the University of Michigan, working with Stephanie Forest now at the University of New Mexico, decided to find out if the genetic algorithm could discover the tit-for-tat strategy. Applying the genetic algorithm first requires translating possible strategies into strings. One simple way is to base the next response on the outcome of the last three plays. Each iteration has four possible outcomes, and so a sequence of three plays yields 64 possibilities. A 64-bit string contains one gene (or bit position) for each. The first gene, for instance, would be allocated to the case of three consecutive mutual defections. The value of each gene would be either 1 or 0 depending on whether the preferred response to its corresponding history was cooperation of defection. For example, the 64-bit string consisting of all 0's would designate the strategy that defects in all cases. Even for such a simple game, there are 264 (approximately 16 quadrillion) different strategies.

Axelrod and Forrest supplied the genetic algorithm with a small random collection of strings representing strategies. The fitness of each string was simple the average of the payoffs its strategy received under repeated play. All these strings had low fitnesses because most strategies for playing the Prisoner's Dilemma are not very good. Quickly the genetic algorithm discovered an exploited tit for tat, but further evolution introduced an additional improvement. The new strategy, discovered while the genetic algorithm was already playing at a high level, exploited players that could be "bluffed" - lured into cooperating repeatedly in the face of defection. It reverted to tit for tat, however, when the history indicated the player could not be bluffed.

Biological evolution operates, of course, not to produce a single superindividual but rather to produce interacting species well adapted to one another. (Indeed, in biological realm there is no such thing as a best individual.) Similarly, the genetic algorithm can be used, with modifications, to govern the evolution not merely of individual rules or strategies but of classifier-system "organisms" composed of many rules. Instead of selecting the fittest rules in isolation, competitive pressures can lead to the evolution of larger systems whose abilities are encoded in the strings that make them up.

Re-creating evolution at this higher level requires several modifications to the original genetic algorithm. Strings still represent condition-action rules, and each rule whose conditions are met generates an action as before. Rating each rule by the number of correct actions it generates, however, will favor the evolution of individual "superrules" instead of finding clusters of rules that interact usefully. To redirect the search toward interacting rules, the procedure is modified by forcing rules to compete for control of the system's actions. Each rule whose conditions are met competes with all other rules whose conditions are met, and the strongest rules determine what the system will do in that given situation. If the system's actions lead to a successful outcome, all the winning rules are strengthened; otherwise they are weakened.

Another way of looking at this method is to consider each rule string as a hypothesis about the classifier's world. A rule enters the competition only when it "claims" to be relevant to the current situation. Its ability to compete depends on how much of a contribution it has made to solving similar problems. As the genetic algorithm proceeds, strong rules mate and form offspring rules that combine their parents' building blocks. These offspring, which replace the weakest rules, amount to plausible but untried hypothesis.

Competition among rules provides the system with a graceful way of handling perpetual novelty. When a system has strong rules that respond to a particular situation, that is the equivalent of saying that it has certain well validated hypothesis. Offspring rules, which begin life weaker than do their parents, can win the competition and influence the system's behavior only when there are no strong rules whose conditions are satisfied - in other words, when the system does not know what to do. If their actions help, the survive; if not , they are soon replaced. Thus, the offspring do not interfere with the system's actions in well-practiced situations but wait gracefully in the wings as hypothesis about what to do under novel circumstances.

Adding competition in this way strongly affects the evolution of a classifier system. Shortly after the system starts running, it evolves rules with simple conditions - treating a broad range of situations as if they were identical. The system exploits such rules as defaults that specify something to be done in the absence of more detailed information. Because the default rules make only coarse discriminations, however, they are often wrong and so do not grow in strength. As the system gains experience, reproduction and crossover lead to the development of more complex, specific rules that rapidly become strong enough to dictate behavior in particular cases.

Eventually the system develops a hierarchy: layers of exception rules at the lower levels handle most cases, but the default rules at the top level of the hierarchy come into play when none of the detailed rules has enough information to satisfy its conditions. Such default hierarchies bring relevant experience to bear on novel situations while preventing the system from becoming bogged down in the overly detailed options.

The same characteristics that make evolving classifier systems adept at handling perpetual novelty also do a good job of handling situations where the payoff for a given action may come only long after the action is taken. The earliest moves of a chess game, for example, may set the stage for later victory of defeat.

To train a classifier system for such long-term goals, a programmer gives the system a payoff each time it completes a task. The credit for success (or the blame for failure) can propagate through the hierarchy to strengthen (or weaken) individual rules even if their actions had only a distant effect on the outcome. Over the course of many generations the system develops rules that act ever earlier to set the stage for later payoffs. It therefore becomes increasingly able to anticipate the consequences of its actions.

Genetic algorithms have now been tested in a wide variety of contexts. David E. Goldberg of the University of Illinois, for example, has developed algorithms that learn to control gas pipeline system modeled on the one that carries natural gas from the Southwest to the Northeast. The pipeline complex consists of many branches, all carrying various amounts of gas; the only controls available are compressors that increase pressure in a particular branch of the pipeline and valves to regulate the flow of gas to and from storage tanks. Because of the tremendous lag between manipulating valves or compressors and the actual pressure changes in the lines, there is no analytic solution to the problem, and human controllers, like Goldberg's algorithm, must learn by apprenticeship.

Goldberg's system not only met gas demand at costs comparable to those achieved in practice, but it also developed a hierarchy of default rules capable of responding properly to holes punched in the pipeline (as happens all to often in reality at the blade of an errant bulldozer). Lawrence Davis of Tica Associates in Cambridge, Mass., has used similar techniques to design communications networks; his software's goals is to carry the maximum possible amount of data with the minimum number of transmission lines and switches interconnecting them.

A group of researchers at General Electric and Rensselaer Polytechnic Institute recently put a genetic algorithm to good use in the design of high-by-pass jet engine turbine such as those that power commercial airliners. Such turbines, which consist of multiple stages of stationary and rotating blade rows enclosed in a roughly cylindrical duct, are at the center of engine-development projects that last five years or more an consume up to $2 billion.



The design of a turbine involves at least 100 variables, each of which can take on a different range of values. The resulting search space contains more than 10387 points. The "fitness" of the turbine depends on how well it satisfies a series of 50 or so constraints, such as the smooth shape of its inner and outer walls or the pressure, velocity and turbulence of the flow at various points inside the cylinder. Evaluating a single design requires running an engine simulation that takes about 30 seconds on a typical engineering workstation.

In one fairly typical case, an engineer working alone took about eight weeks to reach a satisfactory design. So-called expert systems, which use inference rules based on experience to predict the effects of a change of one or two variables, can help direct the designer in seeking out useful changes. An engineer using such an expert system took less than a day to design an engine with twice the improvements of the eight-week manual design.

Such expert systems, however, soon get stuck at points where further improvements can be made only by changing many variables simultaneously. These dead ends occur because it is practically impossible to sort out all the effects associated with different multiple changes, let alone to specify the regions of the design space within which previous experience remains valid.

To get away from such a point, the designer must find new building blocks for a solution. Here is where the genetic algorithm comes into play. Seeding the algorithm with designs produced by the expert system, an engineer took only two days to find a design with three times the improvements of the manual version (and half again as many as using the expert system alone).

This example points up both a strength and a limitation of simple genetic algorithms: they are at their best when exploring complex landscapes to locate regions of enhanced opportunity. But if a partial solution can be improved further by making changes in a few variables, it is best to augment the genetic algorithm with other, more standard methods.

Although genetic algorithms mimic the effects of natural selection, until now they have operated on a much smaller scale than does biological evolution. My colleagues and I have run classifier systems containing as many as 8,000 rules, but this size is at the low end of viability for natural populations. Large animals that are not endangered may number in the millions, insect populations in the trillions and bacteria in the quintillions or more. These large numbers greatly enhance the advantages of implicit parallelism.

As massively parallel computers become more common, it will be feasible to evolve software populations whose size more closely approaches those of natural species. Indeed, the genetic algorithm lends itself nicely to such machines. Each processor can be devoted to a single string because the algorithm's operations focus on single strings or, at most, a pair of strings during crossover. As a result, the entire population can be processed in parallel.

We still have much to learn about classifier systems, but the work done so far suggests they will be capable of remarkable complex behavior. Rick L. Riolo of the University of Michigan has already observed genetic algorithms that display "latent learning" (a phenomenon in which an animal such as a rat explores a maze without reward and is subsequently able to find food placed in the maze much more quickly).

At the Santa Fe Institute, Forrest, W. Brian Arthur, John H. Miller, Richard G. Palmer and I have used classifier systems to simulate economic agents of limited rationality. These agents evolve to the point of acting on trends in a simple commodity market, producing speculative bubbles and crashes.

The simulated worlds these agents inhabit show many similarities to natural ecosystems: they exhibit counterparts to such phenomena as symbiosis, parasitism, biological "arms races," mimcry, niche formation and speciation. Still other work with genetic algorithms has shed light on the conditions under which evolution will favor sexual or a sexual reproduction. Eventually artificial adaptation may repay its debt to nature by increasing researchers' understanding of natural ecosystems and other complex adaptive systems.