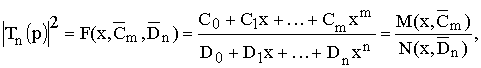Параметрический синтез межкаскадных корректирующих цепей высокочастотных усилителей мощности

Титов А.А., Григорьев Д.А.

Источник:Радиотехника и электроника. – 2003. – № 4. – С. 442–448

 

 

Предложена методика параметрического синтеза межкаскадных корректирующих цепей усилителей мощности ультравысокочастотного и сверхвысокочастотного диапазонов, основанная на методе оптимального синтеза электрических фильтров. Приведены синтезированные таблицы нормированных значений элементов одной из наиболее простых и эффективных межкаскадных корректирующих цепей, применяемых в полосовых усилителях мощности, результаты эксперимента, машинного анализа и оптимизации. Коэффициент усиления одного каскада многокаскадного усилителя мощности ультравысокочастотного и сверхвысокочастотного диапазонов не превышает 3-10 дБ [1-3]. В этом случае увеличение коэффициента усиления каждого каскада, например, на 2 дБ, позволяет повысить коэффициент полезного действия всего усилителя мощности в 1,2-1,5 раза [4].

Современные методы параметрического синтеза усилительных каскадов с межкаскадными корректирующими цепями (МКЦ) не позволяют осуществлять реализацию максимально возможного, для заданного схемного решения, коэффициента усиления, при одновременном обеспечении заданного допустимого уклонения амплитудно-частотной характеристики (АЧХ) от требуемой формы [1, 2, 5-8].

Задача нахождения значений элементов МКЦ, обеспечивающих максимальный коэффициент усиления каскада, в каждом конкретном случае может быть решена с помощью программ оптимизации. Однако наличие хорошего начального приближения значительно сокращает этап последующей оптимизации или делает его излишним [2, 6, 9].

Цель работы – создание методики параметрического синтеза МКЦ усилителей мощности ультравысокочастотного и сверхвысокочастотного диапазонов, позволяющей по таблицам нормированных значений элементов МКЦ осуществлять реализацию усилительных каскадов с максимально возможным, для заданного схемного решения, коэффициентом усиления, при одновременном обеспечении заданного допустимого уклонения АЧХ от требуемой формы.

Согласно [5, 6, 10-12], коэффициент передачи усилительного каскада с МКЦ в символьном виде может быть описан дробно-рациональной функцией комплексного переменного:

где ;
- нормированная частота;
- текущая круговая частота;
- верхняя круговая частота полосы пропускания многооктавного усилителя мощности, либо центральная круговая частота полосового усилителя;

- коэффициенты, являющиеся функциями параметров МКЦ и элементов аппроксимации входного импеданса транзистора усилительного каскада, н

нормированных относительно и сопротивления источника сигнала Rг.

Выберем в качестве прототипа передаточной характеристики (1) дробно-рациональную функцию вида:

(2)

Найдём такие её коэффициенты, которые позволят из системы нелинейных уравнений [10]:

(3)

рассчитать нормированные значения элементов МКЦ, обеспечивающие максимальный коэффициент усиления каскада, при заданном допустимом уклонении его АЧХ от требуемой формы.

В теории усилителей нет разработанной методики расчета коэффициентов ci, dj. Поэтому для их расчета воспользуемся методом оптимального синтеза электрических фильтров [13, 14].

В соответствии с указанным методом перейдем к квадрату модуля функции (2):

где
- вектор коэффициентов ;
- вектор коэффициентов .

При известных значениях коэффициентов функции , коэффициенты функции-прототипа (2) могут быть определены с помощью алгоритма, описанного в [15].

Для решения задачи нахождения векторов коэффициентов составим систему линейных неравенств:

(4)

где  - дискретное множество конечного числа точек в заданной нормированной области частот;
- требуемая зависимость квадрата модуля на множестве ;
- допустимое уклонение от ;
- малая константа.

Первое неравенство в (4) определяет величину допустимого уклонения АЧХ каскада от требуемой формы. Второе и третье неравенства определяют условия физической реализуемости рассчитываемой МКЦ [13]. Учитывая, что полиномы и положительны, модульные неравенства можно заменить простыми и записать задачу в следующем виде:

(5)

Решение неравенств (5) является стандартной задачей линейного программирования. В отличие от теории фильтров, где данная задача решается при условии минимизации функции цели: , неравенства (5) следует решать при условии ее максимизации: , что соответствует достижению максимального значения коэффициента усиления рассчитываемого каскада [16].

Таким образом, предлагаемая методика заключается в следующем:

1. нахождение дробно-рациональной функции комплексного переменного, описывающей коэффициент передачи усилительного каскада с МКЦ;
2. синтез коэффициентов квадрата модуля прототипа передаточной характеристики усилительного каскада с МКЦ по заданным значениям и ;
3. расчет коэффициентов функции-прототипа по известным коэффициентам ее квадрата модуля;
4. решение системы нелинейных уравнений (3) относительно нормированных значений элементов МКЦ.

Многократное решение системы линейных неравенств (5) для различных и позволяет осуществить синтез таблиц нормированных значений элементов МКЦ, по которым ведется проектирование усилителей.

Известные схемные решения построения МКЦ усилителей мощности отличаются большим разнообразием. Однако из-за сложности настройки и высокой чувствительности характеристик усилителей к разбросу параметров сложных МКЦ в усилителях мощности ультравысокочастотного и сверхвысокочастотного диапазонов практически не применяются МКЦ более четвертого-пятого порядка. [1-3, 5, 6, 11, 17, 18].

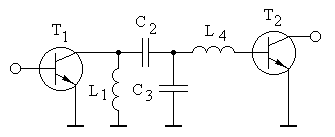
Воспользуемся описанной выше методикой параметрического синтеза мощных усилительных каскадов с МКЦ для синтеза таблиц нормированных значений элементов одной из наиболее простых и эффективных МКЦ, применяемых в полосовых усилителях мощности [3, 17, 18], схема которой приведена на рис. 1.

Рис.1. Реактивная межкаскадная корректирующая цепь четвертого порядка

Для нахождения коэффициента передачи усилительного каскада на транзисторе T2 аппроксимируем входной и выходной импедансы транзисторов T1 и T2 RC- и RL- цепями [1, 5, 10, 12], и от схемы, приведенной на рис. 1, перейдем к схеме, приведенной на рис. 2.

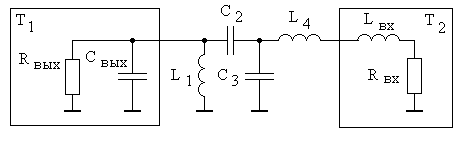
Рис. 2. Эквивалентная схема включения межкаскадной корректирующей цепи

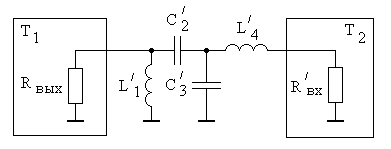
Вводя идеальный трансформатор после конденсатора С2 с последующим применением преобразования Нортона [5], перейдем к схеме, представленной на рис. 3.

Рис. 3. Преобразованная эквивалентная схема включения межкаскадной корректирующей цепи

Для полученной схемы, в соответствии с [5, 6, 10-12], коэффициент передачи последовательного соединения МКЦ и транзистора T2 можно описать выражением:

, (6)

где ;
Gном12 - коэффициент усиления транзистора T2 по мощности в режиме двустороннего согласования на частоте =1 [5];

(7)

(8)

- нормированные относительно и Rвых значения элементов .

По известным значениям , переходя от схемы на рис. 3 к схеме на рис. 2, найдём:

(9)

где ;
Lвхн - нормированное относительно Rвых и значение Lвх.

Из (6) следует, что коэффициент усиления каскада на частоте =1 равен:

(10)

В качестве прототипа передаточной характеристики (6) выберем функцию:.

 (11)

Квадрат модуля функции-прототипа (11) имеет вид: . (12)

Для нахождения коэффициентов Di составим систему линейных неравенств (5):

(13)

Решая (13) для различных и при условии максимизации функции цели: Fun=D4=max, найдем коэффициенты , соответствующие различным полосам пропускания полосового усилительного каскада. Вычисляя полиномы Гурвица знаменателя функции (12) [15], определим коэффициенты функции-прототипа (11).

Значения коэффициентов функции-прототипа (11), соответствующие различным величинам относительной полосы пропускания, определяемой отношением fв/fн, где fв, fн - верхняя и нижняя граничные частоты полосового усилителя, и для неравномерности АЧХ, равной +- 0,5 дБ, приведены в таблице. Здесь же представлены результаты вычислений нормированных значений элементов , полученные из решения системы неравенств (3) и соответствующие различным значениям .

Анализ полученных результатов позволяет установить следующее. При заданной относительной полосе пропускания существует определенное значение , при превышении которого реализация каскада с требуемой формой АЧХ становится невозможной. Это обусловлено уменьшением добротности рассматриваемой цепи с увеличением . При больших величинах отношения fв/fнанализируемая схема МКЦ перерождается в трехэлементную МКЦ, методика расчета которой описана в [11]. Поэтому в таблице приведены результаты расчетов нормированных значений элементов МКЦ, ограниченные отношением fв/fн, равным шести.

Рассматриваемая МКЦ (рис. 1) может быть использована и в качестве входной корректирующей цепи усилителя. В этом случае при расчетах следует полагать Rвых=Rг, Свых=0.

Литература

1. Гребенников А.В., Никифоров В.В. Транзисторные усилители мощности для систем подвижной радиосвязи метрового и дециметрового диапазонов волн // Радиотехника. – 2000 - № 5. – С. 83 – 86.
2. Гребенников А.В., Никифоров В.В., Рыжиков А.Б. Мощные транзисторные усилительные модули для УКВ ЧМ и ТВ вещания // Электросвязь. – 1996. - № 3. – С. 28 – 31.
3. Асессоров В.В., Кожевников В.А., Асеев Ю.Н., Гаганов В.В. Модули ВЧ усилителей мощности для портативных средств связи // Электросвязь. – 1997. - № 7. – С. 21 – 22.
4. Титов А.А. Обеспечение повышенного КПД в транзисторных усилителях мощности класса А // Сб. «Приемно-усилительные устройства СВЧ» / Под ред. А.А. Кузьмина. – Томск: Том. гос. ун-т, 1985. – С. 110 – 113.
5. Бабак Л.И., Пушкарев В.П., Черкашин М.В. Расчет сверхширокополосных СВЧ усилителей с диссипативными корректирующими цепями // Известия вузов. Радиоэлектроника. – 1996. – Том 39. - № 11. - С. 20 – 28.
6. Шахгильдян В.В., Шумилин М.С., Козырев В.Б. и др. Проектирование радиопередатчиков / Под ред. В.В. Шахгильдяна. – М.: Радио и связь, 2000. – 656 с.
7. Sun Y., Fidler J.K. Design method for impedance matching networks // IEE Proc. Circuits, Devices and Syst. – 1996. - Vol. 143. – No. 4. – P. 186 – 194.
8. Dehollain C., Neirynck J. Simplified impedance broadband matching by the image parameter method: The RC case // Int. J. Circuit Theory and Appl. – 1995. – Vol. 23. – No. 2. – P. 91 – 116.
9. Howard A. Higher manufacturing yields using DOE // Microwave J. – 1994. – Vol. 37. – No. 7. – P. 92 – 98.
10. Бабак Л.И., Шевцов А.Н., Юсупов Р.Р. Пакет программ автоматизированного расчета транзисторных широкополосных и импульсных УВЧ - и СВЧ усилителей // Электронная техника. Сер. 1. СВЧ – техника. – 1993. – Вып. 3. – С. 60 – 63.
11. Титов А.А. Расчет межкаскадной корректирующей цепи многооктавного транзисторного усилителя мощности. // Радиотехника. – 1987. - №1. – С. 29 – 31.
12. Ku W.H., Petersen W.C. Optimum gain-bandwidth limitation of transistor amplifiers. // IEEE Trans. – 1975. – Vol. CAS - 22. – No. 6. – P. 523 – 533.
13. Ланнэ А.А. Оптимальный синтез линейных электронных схем. – М.: Связь, 1978. – 336 с.
14. Трифонов И.И. Расчет электронных цепей с заданными частотными характеристиками. – М.: Радио и связь, 1988. – 304 с.
15. Балабанян Н. Синтез электрических цепей. – М.: Госэнергоиздат, 1961.
16. Смирнов Р.А. Оптимизация параметров импульсных и широкополосных усилителей. – М.: Энергия, 1976. – 200 с.
17. Титов А.А. Двухканальный усилитель мощности с диплексерным выходом // Приборы и техника эксперимента. – 2001. – № 1. – С. 68 – 72.
18. Титов А.А., Бабак Л.И., Черкашин М.В. Расчет межкаскадной согласующей цепи транзисторного полосового усилителя мощности. // Электронная техника. Сер. 1. СВЧ-техника. – 2000. - №1. – С. 46 – 50.
19. Бородин Б.А., Ломакин В.М., Мокряков В.В. и др. Мощные полупроводниковые приборы. Транзисторы: Справочник / Под ред. А.В. Голомедова. – М.: Радио и связь, 1985. – 560 с.
20. Фано Р. Теоретические ограничения полосы согласования произвольных импедансов: Пер. с англ. / Под ред. Г.И. Слободенюка. – М.: Сов. радио, 1965.