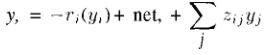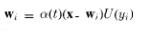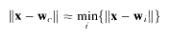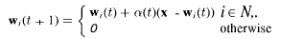Перевод Гринченко А. А.
Оригинал книги расположен по адресу http://www.ru.lv/~peter/ebooks.html

ОБРАБОТКА ДАННЫХ В СОК (Самоорганизующихся картах)

Латеральные взаимодействия среди элементов схемы процесса, окружающих центральный элемент, были промоделированы в Главе 6 – единственная положительная обратная связь шла к центральному элементу, отрицательные обратные связи шли к остальным элементам в слое. В этой главе мы модифицируем ту модель так, что в процессе обучения, положительная обратная связь будет идти от центрального нейрона-победителя к некоторым определенным соседям вокруг него. В конкурентноспособном слое сетей встречного распространения только нейрон-победитель (единственный чей весовой вектор наиболее соответствует входному вектору) может обучаться; в СОК все соседние нейроны, получающие положительную обратную связь от нейрона-победителя, участвуют в процессе обучения. Даже если вес соседнего нейрона ортогонален входному вектору, он будет изменяться под воздействием входного вектора. Это простое дополнение к процессу соревнования достаточно для учета в упорядоченных картах, описанных в предыдущем разделе.

Активация нейронов

Активации элементов процесса определены набором уравнений:

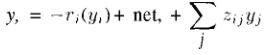
Функция r_i(y_i) общая форма утерянного элемента. В предыдущих примерах описания соревнующихся взаимодействий мы обычно использовали r_i(y_i)= Ay_i, где А – константа (см. Уравнение 6.13), но r_i(y_i) может быть более сложной функцией от y_i . Член уравнения net, входящий в i-й нейрон, вычисляется обычно как входящий вектор точек и весовой вектор нейрона. Последний член уравнения отображает латеральные взаимодействия между нейронами. Суммирование происходит по всем нейронам системы. Если z_ij принимает форму функции «Мексиканской шляпы», изображенной на рисунке 7.2(а), то сеть покажет бурлящую активность вокруг нейрона с наибольшим значением входного вектора. Хотя технически, нейрон с наибольшим значением входного вектора является победителем в соревнующихся системах, его соседи разделяют победу вместе с ним.

Алгоритм обучения СОК

В процессе периода обучения, каждый нейрон с положительной активностью, соседствующий с нейроном победителем, принимает участие в процессе обучения способом, идентичным способу, описанному в Главе 6. Мы можем описать процесс обучения следующим уравнением:

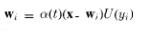
Где w_i – весовой вектор i-ого нейрона, x – входной вектор. Функция U(y_i) равна 0, если y_i > 0 то U(y_i) = 1, это гарантирует что только нейроны с положительной активностью участвуют в процессе обучения. Параметр alfa(t) обозначен как функция от времени, чтобы подчеркнуть что он изменяется в процессе обучения.
В конце дискуссии мы не покажем явно запретные связи между нейронами и мы проигнорирует далеко распространяющиеся возбуждения нейронов при первой аппроксимации. Результирующая функция взаимодействия изображена на рисунке 7.2(б).
Чтобы продемонстрировать формирование упорядоченной характеристики карты, мы будем использовать пример в котором нейроны учатся распознавать свои родственные связи в двумерном пространстве. Сценарий, иллюстрирующий это представлен на фрагменте рисунка 7.3. Каждый элемент процесса определяется его координатами (u,v) в двумерном пространстве. Весовые векторы элементов процесса в этом примере также представлены в двумерном пространстве и их начальные значения установлены случайно.
Как и в других соревнующихся структурах, нейрон победитель определяется для каждого входного вектора и базируется на подобии между входным вектором и весовым вектором. Для входного вектора x нейрон победитель может быть определен как

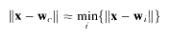
Где индекс с относиться к нейрону победителю. Чтобы свести подписи к минимуму мы определим каждый нейрон в двумерном массиве с единственной подписью как в уравнении 7.3.
Вместо обновления веса только нейрона победителя, мы определяем физически расположенных соседей вокруг него, и все нейроны расположенные в пределах соседства принимают участие в процессе обновления весов. В процессе обучения размер соседства сокращается до тех пор пока не охватит всего один элемент. Если с это нейрон победитель, а N_i это список индексов нейронов соседей, то уравнение обновления весов выглядит таким образом:

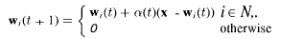
Каждый весовой вектор, участвуя в процессе обновления, немного поворачивается к входящему вектору х. Один процесс обучения достаточно прогрессивный, весовой вектор каждого нейрона сходиться к значению, которое представлено координатами точки близким к физическому расположению нейрона.

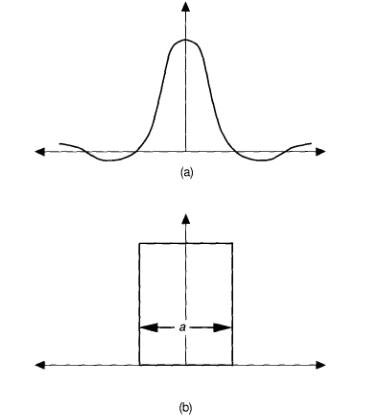
Рисунок 7.2
(б) эти графики иллюстрируют две различные модели латерального взаимодействия между нейронами сети. (а) эта кривая характеризует латеральное взаимодействие между некоторыми нейронами в коре головного мозга, представленное в виде функции «Мексиканской шляпы». Центральный возбуждающий нейрон передает небольшой импульс возбуждения окружающим соседям с положительной обратной связью. Так как боковые расстояния от центрального узла увеличиваются, градус возбуждения снижается пока не перерастет в торможение. Это торможение распространяется на значительно большое расстояние. Наконец, слабая положительная отдача растягивается на большое расстояние от центрального узла. Мы будем использовать эту простую функцию в виде «Мексиканской шляпы» при первой аппроксимации. Расстояние а определяется расстоянием от центрального нейрона до окружающих его соседей, участвующих в процессе обучения наряду с центральным нейроном.

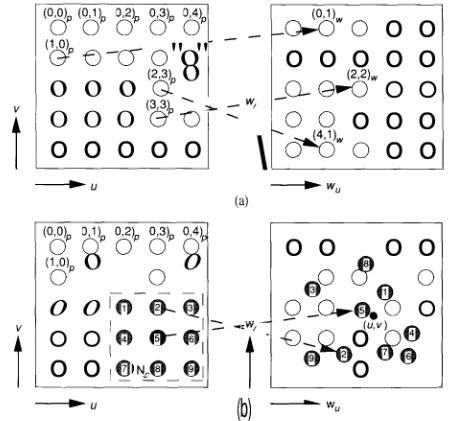
Рисунок 7.3.
Серия этих рисунков показывает процесс обучения в СОК. (а) нейроны самоорганизующейся карты располагаются в пределах двумерного массива дискретных точек (u,v).

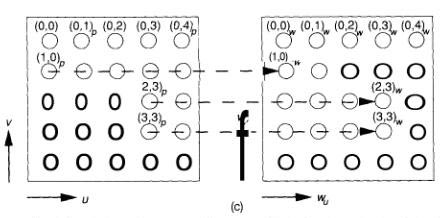
Рисунок 7.3. (продолжение)
Двумерный весовой вектор (w_u, w_i)_U, устанавливается для каждого нейрона. Значение веса соответствует физическому расположению в пределах элементов, участвующих в процессе обучения, но оно устанавливается случайно. Следовательно, нейроны которые в физическом пространстве расположены по соседству, могут не занимать родственные позиции в весовом пространстве. (б) в процессе обучения входные координаты (u,v) выбираются случайно. Нейрон победитель определяется единственной величиной Эвклидового расстояния между выбранной точкой и весовым вектором нейрона и между соседом N_c , физически расположенным по соседству с нейроном победителем. Весовые вектора всех нейронов расположенных по соседству с нейроном победителем, немного изменяются к значению входного вектора (u,v). Обучение продолжается на различном наборе входных векторов, размер соседства постепенно сужается пока не охватит всего один нейрон. (в) в завершении обучения весовой вектор каждого нейрона будет приблизительно равен физическим координатам нейрона.

Кохонен развил хитрый способ изображения динамики процесса обучения на примере проиллюстрированном на рисунке 7.3. вместо того, чтобы проектировать позиции нейронов согласно их физическому расположению, мы можем спроектировать их относительно их расположению в весовом пространстве. Тогда мы рисуем соединительные линии между нейронами, соседствующими в физическом пространстве. Рисунок 7.4 иллюстрирует эту идею. Как развивается карта в процессе обучения показано на рисунке 7.5.
На протяжении нашей дискуссии мы допустили что входные точки выбираются случайно из равномерного распределения установленного в пределах прямоугольной площади, в которой расположены нейроны, участвующие в процессе. Предположим, что входные точки были выбраны из различных распределений, изображенных на рисунке 7.6. В этом случае входные точки выбраны из равномерного треугольного распределения. При этом нейроны процесса сами остаются в двумерном пространстве, но их веса формируют карту треугольной формы. Запомните, что нейроны не изменяют из физического расположения в процессе обучения.

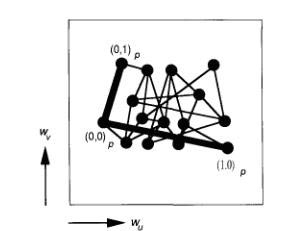
Рисунок 7.4
Каждый нейрон определяется координатами: фиксированной координатой (u,v) в физическом пространстве и варьирующейся координатой (w_u, w_i)_u, в весовом пространстве. Проекции точек построены согласно их позициям в весовом пространстве. Нейроны соединяются линиями соответственно их позициям в физическом пространстве. Толстыми линиями показано соединение соседних нейронов (0, 0)_p, (0, 1)_p, и (1, 0)_p .

Во введении этой главы мы говорили об использовании СОК для сокращения размерности многомерного пространства входных векторов до двумерного пространства. Мы можем продемонстрировать эту идею нанесением двумерного массива точек на одномерный массив элементов процесса. Рисунок 7.7 иллюстрирует выбор между двумя распределениями входных точек. Необходимо запомнить, что входные и весовые вектора оба двумерные, тогда как физическое расположение каждого элемента процесса обучения представлено одномерным массивом.
Все наши примеры к этому моменту использовали входные точки, равномерно распределенные в пределах какого-либо региона. И в использовании равномерного распределения нет ничего сокровенного. Входные точки могут быть распределены согласно любой функции распределения. Как только СОК обучиться, весовые векторы станут систематизированы приблизительно согласно функции распределения входных векторов. В более формальных источниках зафиксировано, что плотность функции весовых векторов точек имеет тенденцию к приближению плотности функции вероятности p(x) входных векторов x, и весовые векторы имеют тенденцию упорядочиваться согласно их взаимному подобию.
Мы не будем пытаться доказывать, что описанное выше приведет в результате к сохраняющей топологию карте. Даже для простого одномерного случая такое доказательство чрезвычайно долгое и сложное. Для углубления вы можете обратиться к великолепной книге Кохонена .

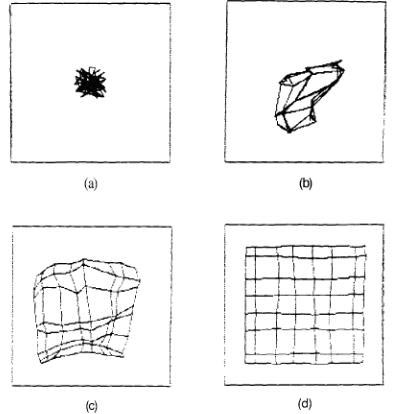
Рисунок 7.5
В этом ряду фигур, двумерная СОК развивается от пространства входных точек, выбранных случайным образом из однородного прямоугольного распрделения. (а) в начале карты весовые вектора имеют случайные значения возле центральных координат карты. (б) так как карта начинает развиваться, веса распространяются от центра (в) в конечном счете структура карты начинает выясняться (г) в конце связи между весовыми векторами имитируют связи между физическими координатами элементов процесса.