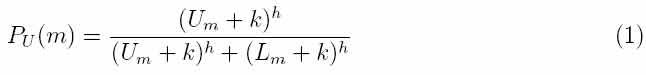| Faculty of Computer Information Тechnologies & Аutomation |
 |
|
 |
Khaustova DaryaSpeciality: Information control systems and technologiesTheme of master's work: Development of computer subsystem for decision-making during planning and distributing construction worksLeader of work: associate professor Svetlichnaya Viktoriya Antonovna | |
 |
bestdash@yandex.ru 387720857 387720857 |
|
| |||
| |||
|
Active development of new construction leads to search of newest methods of planning, organization and distribution of construction works.
Ant algorithms were first proposed by Dorigo and colleagues as a multi-agent approach to difficult combinatorial optimization problems like the traveling salesman problem (TSP) and the quadratic assignment problem (QAP). There is currently a lot of ongoing activity in the scientific community to extend/apply ant-based algorithms to many different discrete optimization problems. Recent applications cover problems like vehicle routing, sequential ordering, graph coloring, routing in communications networks, and so on. So I will use Ant algorithm for optimization of distribution construction works. Ant algorithms were inspired by the observation of real ant colonies. Ants are social insects, that is, insects that live in colonies and whose behavior is directed more to the survival of the colony as a whole than to that of a single individual component of the colony. Social insects have captured the attention of many scientists because of the high structuration level their colonies can achieve, especially when compared to the relative sim- plicity of the colony's individuals. An important and interesting behavior of ant colonies is their foraging behavior, and, in particular, how ants can find shortest paths between food sources and their nest. While walking from food sources to the nest and vice versa, ants deposit on the ground a substance called pheromone, forming in this way a pheromone trail. Ants can smell pheromone and, when choosing their way, they tend to choose, in probability, paths marked by strong pheromone concentrations. The pheromone trail allows the ants to find their way back to the food source (or to the nest). Also, it can be used by other ants to find the location of the food sources found by their nestmates. It has been shown experimentally that this pheromone trail following behavior can give rise, once employed by a colony of ants, to the emergence of shortest paths. That is, when more paths are available from the nest to a food source, a colony of ants may be able to exploit the pheromone trails left by the individual ants to discover the shortest path from the nest to the food source and back. In order to study in controlled conditions the ants' foraging behavior, the binary bridge experiment has been set up by Deneubourg et al.(see Figure 1a). The nest of a colony of ants of the species Linepithema humile and a food source have been separated by a double bridge in which each branch has the same length. Ants are then left free to move between the nest and the food source and the percentage of ants which choose one or the other of the two branches is observed over time. The result (see Figure 1b) is that after an initial transitory phase in which some oscillations can appear, ants tend to converge on a same path. 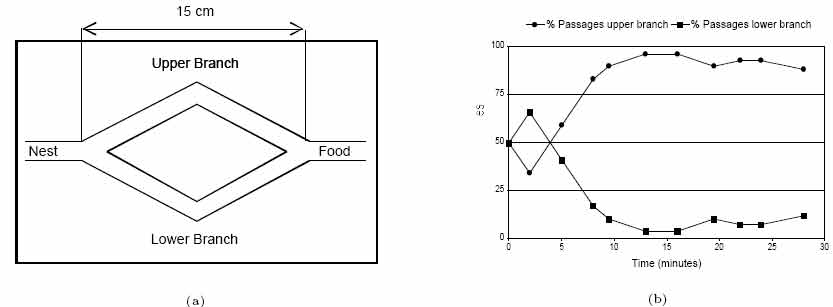 Figure 1. Single bridge experiment. (a) Experimental setup. (b) Results for a typical single trial, showing the percentage of passages on each of the two branches per unit of time as a function of time. Eventually, after an initial short transitory phase, the upper branch becomes the most used. After Deneubourg et al., 1990. In the above experiment initially there is no pheromone on the two branches, which are therefore selected by the ants with the same probability. Nevertheless, random fluc-
tuations, after an initial transitory phase, cause a few more ants to randomly select one
branch, the upper one in the experiment shown in Figure 1a, over the other. Because
ants deposit pheromone while walking, the greater number of ants on the upper branch
determines a greater amount of pheromone on it, which in turn stimulates more ants to
choose it, and so on. The probabilistic model that describes this phenomenon, which
closely matches the experimental observations, is the following. We first make the
assumption that the amount of pheromone on a branch is proportional to the number of
ants that used the branch in the past. This assumption implies that pheromone evapo-
ration is not taken into account. Given that an experiment typically lasts approximately
one hour, it is plausible to assume that the amount of pheromone evaporated in this time
period is negligible. In the model, the probability of choosing a branch at a certain time
depends on the total amount of pheromone on the branch, which in turn is proportional
to the number of ants that used the branch until that time. More precisely, let Um and
Lm be the numbers of ants that have used the upper and lower branch after m ants have
crossed the bridge, with Um + Lm = m. The probability PU (m) with which the (m + 1)-th
ant chooses the upper branch is In this case, because of the same pheromone laying mechanism as in the previous situation, the shortest branch is most often selected: The first ants to arrive at the food source are those that took the two shortest branches, so that, when these ants start their return trip, more pheromone is present on the short branch than on the long branch, stimulating successive ants to choose the short branch. In this case, the importance of initial random fluctuations is much reduced, and the stochastic pheromone trail following behavior of the ants coupled to differential branch length is the main mechanism at work. In Figure 2 are shown the experimental apparatus and the typical result of an experiment with a double bridge with branches of different lengths. 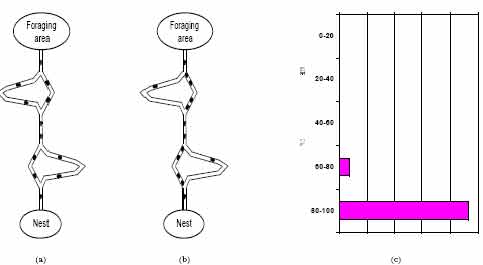 Figure 2. Double bridge experiment. (a) Ants start exploring the double bridge. (b) Eventually most of the ants choose the shortest path. (c) Distribution of the percentage of ants that selected the shorter path. After Goss et al. 1989 It is clear that what is going on in the above described process is a kind of distributed optimization mechanism to which each single ant gives only a very small contribution. It is interesting that, although a single ant is in principle capable of building a solution (i.e., of finding a path between nest and food reservoir), it is only the ensemble of ants, that is the ant colony, which presents the "shortest path finding" behavior. In a sense, this behavior is an emergent property of the ant colony. It is also interesting to note that ants can perform this specific behavior using a simple form of indirect communication mediated by pheromone laying, known as stigmergy . Applications of ACO algorithms to static combinatorial optimization problemsThe application of the ACO meta-heuristic to a static combinatorial optimization problem is relatively straightforward, once defined a mapping of the problem which allows the incremental construction of a solution, a neighborhood structure, and a stochastic state transition rule to be locally used to direct the constructive procedure.
1 procedure ACO Meta heuristic()
2 while (termination criterion not satisfied)
3 schedule activities
4 ants generation and activity();
5 pheromone evaporation();
6 daemon actions(); {optional}
7 end schedule activities
8 end while
9 end procedure
10 procedure ants generation and activity()
11 while (available resources)
12 schedule the creation of a new ant();
13 new active ant();
14 end while
15 end procedure
16 procedure new active ant() {ant lifecycle}
17 initialize ant();
18 M =update ant memory();
19 while (current state <> target state)
20 A = read local ant-routing table();
21 P = compute transition probabilities(A; M; problem constraints);
22 next state = apply ant decision policy(P ; problem constraints);
23 move to next state(next state);
24 if (online step-by-step pheromone update)
25 deposit pheromone on the visited arc();
26 update ant-routing table();
27 end if
28 M =update internal state();
29 end while
30 if (online delayed pheromone update)
31 evaluate solution();
32 deposit pheromone on all visited arcs();
33 update ant-routing table();
34 end if
35 die();
36 end procedure
The ACO meta-heuristic in pseudo-code. Comments are enclosed in braces. All the procedures at the first level of indentation in the statement in parallel are executed concurrently. The procedure daemon actions() at line 6 is optional and refers to centralized actions executed by a daemon possessing global knowledge. The target state (line 19) refers to a complete solution built by the ant. The step-by-step and delayed pheromone updating procedures at lines 24-27 and 30-34 are often mutually exclusive. When both of them are absent the pheromone is deposited by the daemon. Job-shop scheduling problemColorni, Dorigo and Maniezzo (1994) applied AS to the job-shop scheduling problem
(JSP), which is formulated as follows. Given a set M of machines and a set J of jobs
consisting of an ordered sequence of operations to be executed on these machines, the
job-shop scheduling problem is the problem of assigning operations to machines and time
intervals so that the maximum of the completion times of all operations is minimized and
no two jobs are processed at the same time on the same machine. JSP is NP -hard.
The basic algorithm they applied was exactly the same as AS, where the | |||
|
Top
|