Обязательным элементом замкнутой системы управления является обратная связь. При регулировании величины какого-либо параметра осуществляется измерение фактического значения этого параметра и устанавливается его отклонение от заданного уровня. Это отклонение иногда называют рассогласованием. В том случае, когда управляющий механизм усиливает обнаруженное рассогласование, говорят, что имеет место положительная обратная связь, а когда уменьшает — отрицательная. Отрицательная обратная связь используется, например, в регуляторе Уатта, а положительная — в некоторых тормозных системах. Использованию обратной связи для управления в кибернетике уделяется очень большое внимание. Это объясняется тем, что регулятор с обратной связью является достаточно универсальным. При использовании такого регулятора нет необходимости знать причину возникновения возмущения определенного вида, чтобы в зависимости от нее искать рецепт регулирования. Поясним сказанное примером. Пусть речь идет о регулировании температуры жидкости, находящейся в каком-либо сосуде. Обратная связь позволяет компенсировать колебания температуры жидкости вне зависимости от того, каким источником или потребителем тепла они вызваны. В кибернетике имеют дело с системами, часто неподдающимися детальному описанию. Управлять такими системами можно, только используя принцип обратной связи. При рассмотрении обратной связи ознакомились с одним из методов управления, называемым регулированием. В природе и, в частности, в биологических системах существуют естественные механизмы управления, представляющие собой гомеостаты. Гомеостатом называют устройство, предназначенное для поддержания значений любой переменной в заданных пределах. В гомеостате управляемая переменная поддерживается на требуе¬мом уровне механизмом саморегулирования, обеспечивающим целенаправленное приспособление системы к возмущениям. Целью самонастройки может быть обеспечение заданных показателей качества управляющей системы (качество готовой продукции) либо поддержание экспериментальных значений (минимизация затрат на производство при заданном качестве производимой продукции). При этом алгоритм управления автоматически и целенаправленно изменяет параметры для обеспечения наилучшим управлением объектом. Автоматические регуляторы промышленной автоматики, функционирующие на основе линейных или нелинейных законов регулирования, успешно удерживают регулируемые объекты в заданном состоянии, хотя располагают только неполной информацией о технологическом процессе и структуре объекта. Возможности регуляторов в этом отношении можно пояснить характерным примером. Распределенность параметров, нелинейная зависимость теплофизических свойств стали и параметров теплообмена от температуры делают эту задачу весьма сложной. Между тем, установленный автоматический регулятор, реализующий алгоритм регулирования с отрицательной обратной связью, через короткий промежуток времени после включения устанавливает требуемый режим охлаждения, т. е. автоматически решает рассматриваемую задачу. 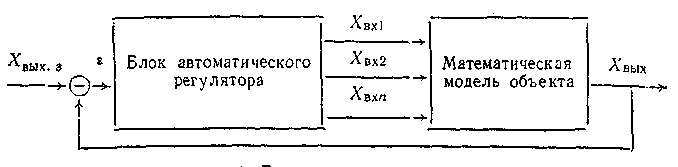 Рисунок 1 – Блок-схема автоалгоритма
где Xвх1, Хвх2, Хвх1 — искомые входные величины; Хвых.3 — заданное значение выходной величины; E —ошибка вычислений. В связи с этим представляется целесообразным в сложных случаях осуществлять динамическое моделирование на базе алгоритма, который в дальнейшем будем называть автоалгоритмом (рис. 1). Основные принципы автоалгоритмизации расчетов заключаются в следующем: 1) для организации расчетов составляют структурную схему (математическую модель) рассматриваемой системы с указанием входных (независимых) и выходных (зависимых) переменных системы; статическая зависимость между выходными и входными величинами должна быть монотонной; 2) в блок-схему системы включают блок автоматического регулятора, причем на его вход поступает разность между заданным и текущим значениями выходной величины системы (ошибка расчета), а выходом регулятора является целенаправленное изменение входной величины системы, ведущее к уменьшению ошибки расчета; 3) алгоритм функционирования системы с регулятором реализуют на ЭВМ, и расчеты выполняют до тех пор, пока выходная величина системы не достигнет установившегося значения, равного заданному в пределах допустимой погрешности расчета; входная величина системы в установившемся состоянии является искомой величиной. Если обычно объект моделируется для поиска оптимального закона управления им, то в нашем случае будет наблюдаться обратное: модель системы управления будет использоваться для моделирования, исследования и расчета производственного агрегата. Решение задачи управления сводится к созданию управляющей системы, которая будет осуществлять управление рассматриваемым объектом. При создании управляющей системы используют ряд принципов. Один из них — принцип обратной связи — мы рассмотрели выше. Предположим, что имеется управляющая система с обратной связью. Это обратная связь следит за изменением выходного управляемого параметра Y. Предположим, что Y зависит от нескольких входных величин (х1 , х2 , . . ., хi , хт) и что среди хi имеются случайные величины, не поддающиеся нашему контролю. Оказывается, что для управления параметром Y нет необходимости воздействовать на каждое xi. Для решения этой задачи достаточно найти так называемый главный фактор и воздействовать только на него. Это и есть принцип управления воздействием на главный фактор. |