В настоящее время наиболее распространенным способом управления охлаждением НЛЗ является управление по графикам: зависимостям расхода воды от скорости разливки для заданных марок стали. При отлаженной технологии и стабильном химическом составе металла этого вполне достаточно. Но при появлении новых марок стали или изменении исходных параметров металла или МНЛЗ требуется проведение отдельных исследовательских работ для определения новых графиков охлаждения. Кроме того, на предельных скоростях разливки при колебании химического состава и температуры металла существующие графики могут не обеспечивать требуемое охлаждение НЛЗ, что приводит к ухудшению качества заготовки. Использование математической модели процесса разливки при управлении охлаждением НЛЗ позволяет сократить время ввода новых марок стали и стабилизировать качество заготовок при изменении входных параметров разливки (температуры, химического состава, зон охлаждения), повысить серийность разливки. Наиболее полную и точную информацию о состоянии НЛЗ можно получить, используя численные методы при моделировании процесса разливки. Но и здесь есть свои сложности:
В настоящее время на Молдавском Металлургическом Заводе разработана математическая модель процесса охлаждения НЛЗ и создана программа управления ЗВО с ее использованием. В основу модели заложен Метод Конечных Элементов с расчетом по схеме Кранка-Николсона, позволяющий достигнуть точности расчетов менее 5 %. Параметры теплообмена в зонах вторичного охлаждения и кристаллизаторе определялись экспериментально, с учетом существующих зависимостей. Так, например, теплоотдача в кристаллизаторе определялась как экспоненциальная зависимость теплового потока от времени [1], а коэффициент теплоотдачи ЗВО определялся как линейная зависимость от плотности орошения [2]. Внешний вид программы расчета температурного поля НЛЗ представлен на рис. 1. На рабочем окне отображаются:
Исходными данными для математического расчета являются химический состав и температура металла, скорость разливки и расходы воды в зонах охлаждения. После расчета температуры по длине заготовки происходит сравнение полученных значений с заданным (или рассчитанным по критериям качества) температурным профилем, по результатам сравнения происходит корректировка расхода воды на ЗВО. На больших скоростях при вероятности появления жидкой фазы во время реза выдается предупреждение и рекомендация снизить скорость разливки. Модель адаптируется к заготовкам любого размера и профиля. Настройка на конкретную МНЛЗ происходит с использованием стационарно установленных пирометров, расположенных по длине заготовки. Как правило, позиции установки соответствуют окончанию каждой зоны охлаждения. Настраиваемыми параметрами являются коэффициенты теплоотдачи ЗВО и кристаллизатора. Пример такой настройки для условий МНЛЗ-2 Молдавского металлургического завода представлен на рисунках 2 и 3. 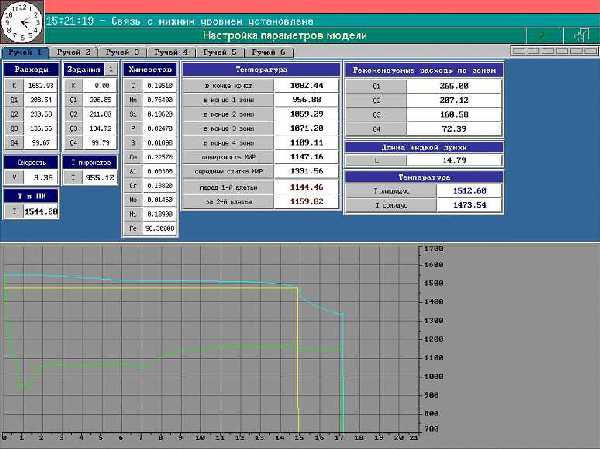 Рисунок 1 – Рабочее окно программы расчета температурного поля НЛЗ. (голубая линия – температура сердцевины слитка; зеленая линия температура поверхности слитка; желтая линия – протяженность жидкой фазы по длине НЛЗ) 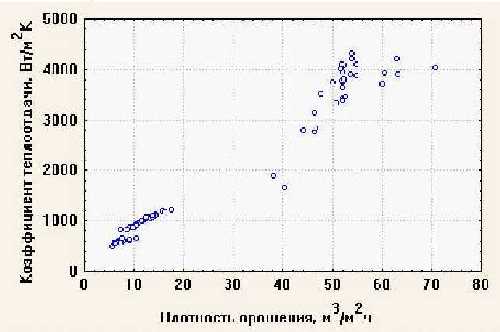 Рисунок 2 – Экспериментальное определение зависимости коэффициента теплоотдачи ЗВО от плотности орошения 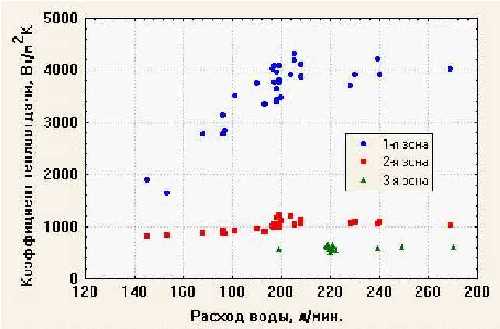 Рисунок 3 – Экспериментальное определение зависимости коэффициента теплоотдачи ЗВО от расхода воды на ЗВО 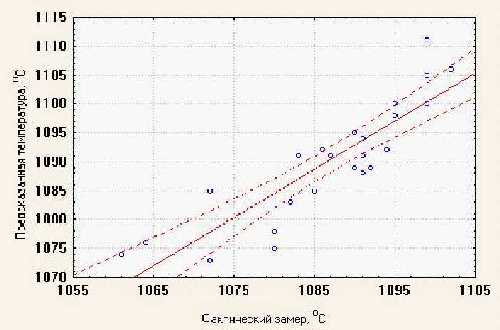 Рисунок 4 – Корреляционная зависимость между фактической и расчетной температурами (коэффициент корреляции: r = 0.88) Достоверные результаты расчета позволяют широко использовать модель в автоматизированной системе управления предприятием. К возможным областям ее применения относятся:
В настоящее время модель настроена на работу с низко- и среднеуглеродистыми марками стали. О качестве ее работы можно судить по рис.4. После проведения дополнительных исследований теплофизических параметров металла область применения модели будет расширена и на высокоуглеродистые марки стали. В результате выполненных исследований установлено, что для водяного форсуночного охлаждения коэффициент теплоотдачи ЗВО линейно зависит от плотности орошения до значения 40 м3/м2ч, а выше 55 м3/м2ч он стабилизируется. Использование математической модели при управлении зонами вторичного охлаждения позволяет стабилизировать качество НЛЗ и повысить серийность разливки. Список литературы 1. Л. Шмрга «Затвердевание и кристаллизация стальных слитков» М: Металлургия, 1985 г.-248 с. 2. В.А. Емельянов «Тепловая работа машин непрерывного литья заготовок», М.: Металлургия, 1988г.-141 с. |