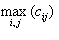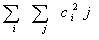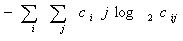|
АВТОРЕФЕРАТ
|
Source: R.Gonzalez, R. Woods "Digital Image Processing"
http://www.imageprocessingplace.com/dip3e_sample_book_material/dip3e_preface.pdf
1.3.3 Texture
An important approach to region description is to quantify its texture content. Although no formal definition of texture exists, intuitively this descriptor provides measures of properties such as smoothness, coarseness, and regularity (Fig. 11.22 shows some examples). The three principal approaches used in image processing to describe the texture of a region are statistical, structural, and spec¬tral. Statistical approaches yield characterizations of textures as smooth, coarse,
 FIGURE 11.22 The while squares mark, from left lo right, smooth, coarse, and regular textures. These are optical microscope images of a superconductor, human cholesterol, and a microprocessor. (Courtesy of Dr. Michael W. Davidson, Florida Stale University.) where m is the mean value of z (the average gray level):
FIGURE 11.22 The while squares mark, from left lo right, smooth, coarse, and regular textures. These are optical microscope images of a superconductor, human cholesterol, and a microprocessor. (Courtesy of Dr. Michael W. Davidson, Florida Stale University.) where m is the mean value of z (the average gray level):
grainy, and so on. Structural techniques deal with the arrangement of image primitives, such as the description of texture based on regularly spaced parallel lines. Spectral techniques are based on properties of the Fourier spectrum and are used primarily to detect global periodicity in an image by identifying high-energy, narrow peaks in the spectrum.
Statistical approaches
One of the simplest approaches for describing texture is to use statistical moments of the gray-level histogram of an image or region. Let z be a random variable denoting gray levels and let 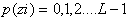 , be the corresponding histogram, where L is the number of distinct gray levels. From Eq. (3.3-18), the nth moment of z about the mean is , be the corresponding histogram, where L is the number of distinct gray levels. From Eq. (3.3-18), the nth moment of z about the mean is  where m is the mean value of z (the average gray level):
where m is the mean value of z (the average gray level):
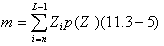 Note from Eq. (11.3-4) that
Note from Eq. (11.3-4) that 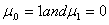 .The second moment [the variance .The second moment [the variance 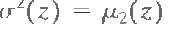 ] is of particular importance in texture description. It is a measure of gray-level contrast that can be used to establish descriptors of relative smoothness. For example, the measure ] is of particular importance in texture description. It is a measure of gray-level contrast that can be used to establish descriptors of relative smoothness. For example, the measure 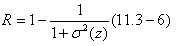 is 0 for areas of constant intensity (the variance is zero there) and approaches 1 for large values of
is 0 for areas of constant intensity (the variance is zero there) and approaches 1 for large values of 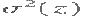 Because variance values tend to be large for grayscale images with values, for example, in the range 0 to 255, it is a good idea to normalize the variance to the interval [0,1 ] for use in Eq. (11.3-6).This is done simply by dividing Because variance values tend to be large for grayscale images with values, for example, in the range 0 to 255, it is a good idea to normalize the variance to the interval [0,1 ] for use in Eq. (11.3-6).This is done simply by dividing  in Eq. (11.3-6).The standard deviation also is used frequently as a measure of texture because values of the stan¬dard deviation tend to be more intuitive to many people. The third moment,
is a measure of the skewness of the histogram while the fourth moment is a measure of its relative flatness. The fifth and higher moments are not so easily related to histogram shape, but they do provide further quantitative discrimination of texture content. Some useful additional texture measures based on histograms include a measure of "uniformity," given by in Eq. (11.3-6).The standard deviation also is used frequently as a measure of texture because values of the stan¬dard deviation tend to be more intuitive to many people. The third moment,
is a measure of the skewness of the histogram while the fourth moment is a measure of its relative flatness. The fifth and higher moments are not so easily related to histogram shape, but they do provide further quantitative discrimination of texture content. Some useful additional texture measures based on histograms include a measure of "uniformity," given by
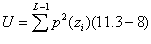 and an average entropy measure, which the reader might recall from basic information theory, or from our discussion in Chapter 8, is defined as
and an average entropy measure, which the reader might recall from basic information theory, or from our discussion in Chapter 8, is defined as
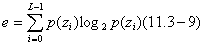 Because thep's have values in the range [0,1] and their sum equals 1, measure U is maximum for an image in which all gray levels are equal (maximally uniform), and decreases from there. Entropy is a measure of variability and is 0 for a constant image.
Table 11.2 summarizes the values of the preceding measures for the three types of textures highlighted in Fig. 11.22. The mean just tells us the average gray level of each region and is useful only as a rough idea of intensity, not really texture. The standard deviation is much more informative; the numbers clearly show that the first texture has significantly less variability in gray level (it is smoother) than the other two textures. The coarse texture shows up clearly in this measure. As expected, the same comments hold for R, because it measures essentially the same thing as the standard deviation. The third moment generally is useful for determining the degree of symmetry of histograms and whether they are skewed to the left (negative value) or the right (positive value).
Because thep's have values in the range [0,1] and their sum equals 1, measure U is maximum for an image in which all gray levels are equal (maximally uniform), and decreases from there. Entropy is a measure of variability and is 0 for a constant image.
Table 11.2 summarizes the values of the preceding measures for the three types of textures highlighted in Fig. 11.22. The mean just tells us the average gray level of each region and is useful only as a rough idea of intensity, not really texture. The standard deviation is much more informative; the numbers clearly show that the first texture has significantly less variability in gray level (it is smoother) than the other two textures. The coarse texture shows up clearly in this measure. As expected, the same comments hold for R, because it measures essentially the same thing as the standard deviation. The third moment generally is useful for determining the degree of symmetry of histograms and whether they are skewed to the left (negative value) or the right (positive value).
 This gives a rough idea of whether the gray levels are biased toward the dark or light side of the mean. In terms of texture, the information derived from the third moment is useful only when variations between measurements are large. Looking at the measure of uniformity, we again conclude that the first subimage is smoother (more uniform than the rest) and that the most random (lowest uniformity) corresponds to the coarse texture.This is not surprising. Finally, the entropy values are in the opposite order and thus lead us to the same conclusions as the uniformity measure did. The first subimage has the lowest variation in gray level and the coarse image the most. The regular texture is in between the two extremes with respect to both these measures.
Measures of texture computed using only histograms suffer from the limitation that they carry no information regarding the relative position of pixels with respect to each other. One way to bring this type of information into the texture-analysis process is to consider not only the distribution of intensities, but also the positions of pixels with equal or nearly equal intensity values.
Let P be a position operator and let A be а к*к matrix whose element is the number of times that points with gray level
This gives a rough idea of whether the gray levels are biased toward the dark or light side of the mean. In terms of texture, the information derived from the third moment is useful only when variations between measurements are large. Looking at the measure of uniformity, we again conclude that the first subimage is smoother (more uniform than the rest) and that the most random (lowest uniformity) corresponds to the coarse texture.This is not surprising. Finally, the entropy values are in the opposite order and thus lead us to the same conclusions as the uniformity measure did. The first subimage has the lowest variation in gray level and the coarse image the most. The regular texture is in between the two extremes with respect to both these measures.
Measures of texture computed using only histograms suffer from the limitation that they carry no information regarding the relative position of pixels with respect to each other. One way to bring this type of information into the texture-analysis process is to consider not only the distribution of intensities, but also the positions of pixels with equal or nearly equal intensity values.
Let P be a position operator and let A be а к*к matrix whose element is the number of times that points with gray level 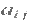 occur (in the position specified by P) relative to points with gray level occur (in the position specified by P) relative to points with gray level 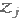 with with 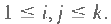 For instance, consider an image with three gray levels, For instance, consider an image with three gray levels,  as follows: as follows:
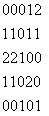 Defining the position operator P as "one pixel to the right and one pixel below" yields the following 3x3 matrix A:
Defining the position operator P as "one pixel to the right and one pixel below" yields the following 3x3 matrix A:
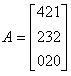 where, for example,
where, for example,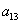 (top left) is the number of times that a point with level (top left) is the number of times that a point with level  appears one pixel location below and to the right of a pixel with the same gray level, and appears one pixel location below and to the right of a pixel with the same gray level, and 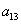 (top right) is the number of times that a point with level (top right) is the number of times that a point with level  .The size of A is determined by the number of distinct gray levels in the input image. Thus application of the concepts discussed in this section usually requires that intensities be requantized into a few gray-level bands in order to keep the size of A manageable. .The size of A is determined by the number of distinct gray levels in the input image. Thus application of the concepts discussed in this section usually requires that intensities be requantized into a few gray-level bands in order to keep the size of A manageable.
-
Maximum probability
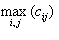
-
Element difference moment of order k

-
Inverse element difference moment of order k

-
Uniformity
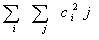
-
Entropy
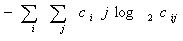
- The basic idea is to characterize the "content" of C via these descriptors. For example, the first property gives an indication of the strongest response to P. The second descriptor has a relatively low value when the high values of C are near the main diagonal, because the differences (i-j) are smaller there. The third descriptor has the opposite effect. The fourth descriptor is highest when the c/s are all equal. As noted previously, the fifth descriptor is a measure of randomness, achieving its highest value when all elements of C are maximally random.
|

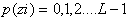 , be the corresponding histogram, where L is the number of distinct gray levels. From Eq. (3.3-18), the nth moment of z about the mean is
, be the corresponding histogram, where L is the number of distinct gray levels. From Eq. (3.3-18), the nth moment of z about the mean is 
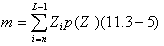
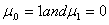 .The second moment [the variance
.The second moment [the variance 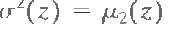 ] is of particular importance in texture description. It is a measure of gray-level contrast that can be used to establish descriptors of relative smoothness. For example, the measure
] is of particular importance in texture description. It is a measure of gray-level contrast that can be used to establish descriptors of relative smoothness. For example, the measure 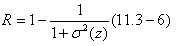
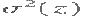 Because variance values tend to be large for grayscale images with values, for example, in the range 0 to 255, it is a good idea to normalize the variance to the interval [0,1 ] for use in Eq. (11.3-6).This is done simply by dividing
Because variance values tend to be large for grayscale images with values, for example, in the range 0 to 255, it is a good idea to normalize the variance to the interval [0,1 ] for use in Eq. (11.3-6).This is done simply by dividing  in Eq. (11.3-6).The standard deviation also is used frequently as a measure of texture because values of the stan¬dard deviation tend to be more intuitive to many people. The third moment,
in Eq. (11.3-6).The standard deviation also is used frequently as a measure of texture because values of the stan¬dard deviation tend to be more intuitive to many people. The third moment,
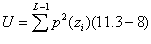
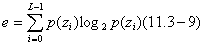

 occur (in the position specified by P) relative to points with gray level
occur (in the position specified by P) relative to points with gray level 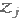 with
with 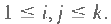 For instance, consider an image with three gray levels,
For instance, consider an image with three gray levels,  as follows:
as follows:
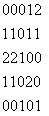
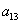 (top left) is the number of times that a point with level
(top left) is the number of times that a point with level  appears one pixel location below and to the right of a pixel with the same gray level, and
appears one pixel location below and to the right of a pixel with the same gray level, and 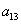 (top right) is the number of times that a point with level
(top right) is the number of times that a point with level  .The size of A is determined by the number of distinct gray levels in the input image. Thus application of the concepts discussed in this section usually requires that intensities be requantized into a few gray-level bands in order to keep the size of A manageable.
.The size of A is determined by the number of distinct gray levels in the input image. Thus application of the concepts discussed in this section usually requires that intensities be requantized into a few gray-level bands in order to keep the size of A manageable.