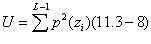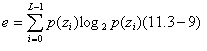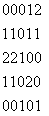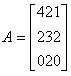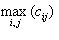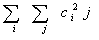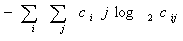|
АВТОРЕФЕРАТ
|
Перевод осуществлялся с книги R.Gonzalez, R. Woods "Digital Image Processing", которую можно скачать на сайте:
http://www.imageprocessingplace.com/dip3e_sample_book_material/dip3e_preface.pdf
1.3.3 Texture
Важный подход к описанию области является текстурное содержание. Несмотря на то что, не существует формального описания текстуры, интуитивно – это описатель, обеспечивающий меру свойств таких как гладкость, грубость и регулярность (на изображении 11.22 показаны некоторые примеры). Три принципиальных подхода используются в обработке изображений при описании текстур области – статистический, структурный и спектральный. Статистический подход описывает характеристики текстуры такие как гладкость, грубость,
 Фигура 11.22 (а), б), в) ) Белые прямоугольные области, слева направо, гладкая, грубая и регулярная текстуры. Это оптические микроскопические изображения сверхпроводника, человеческого холестерина и микропроцессора.
Фигура 11.22 (а), б), в) ) Белые прямоугольные области, слева направо, гладкая, грубая и регулярная текстуры. Это оптические микроскопические изображения сверхпроводника, человеческого холестерина и микропроцессора.
грануированность и др. Структурные методы имеют дело с примитивами изображения, таких как описатель текстуры, основанный на регулярно разделенных параллельных прямых. Спектральный подход основывается на свойствах ряда Фурье и использует преимущественно определение глобальных периодичностей на изображении таких как идентификация высокой энергии или узких пиков в
спектре.
Статистические методы
Один из простых подходов для определения текстуры использование статистических моментов серых уровней гистограммы на изображении или его отдельной области. Пусть z будет случайной величиной, обозначающей серые уровни и пусть p(z), i=0,1,2….L-1 будет передавать гистограмму, где L-это различимых серых уровней. В формуле 3.3-18 nth момент от z по – среднему – это  где m это среднее значение из z (срудний серый уровень):
где m это среднее значение из z (срудний серый уровень):
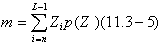 Запомните в формуле 11.3-4 =1 и =0. Второй момент (выражение
Запомните в формуле 11.3-4 =1 и =0. Второй момент (выражение 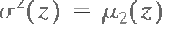 )особенно важен в описании текстуры. Это мера контрастного серого уровня, которая может быть использована для установления описателей относительно гладкости. Для примера, мера )особенно важен в описании текстуры. Это мера контрастного серого уровня, которая может быть использована для установления описателей относительно гладкости. Для примера, мера 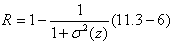 Это 0 для областей с постоянной интенсивностью (изменяемость равна 0 там) и подходит 1 для больших значений
Это 0 для областей с постоянной интенсивностью (изменяемость равна 0 там) и подходит 1 для больших значений 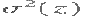 Т.к. значение выражения склоняется к большой серой шкале изображений со значениями, например, в диапозоне от 0 до 255, это хорошая идея для нормализации выражения в интервале [0,1] используемой в формуде 11.3-6. Это делается просто для описания Т.к. значение выражения склоняется к большой серой шкале изображений со значениями, например, в диапозоне от 0 до 255, это хорошая идея для нормализации выражения в интервале [0,1] используемой в формуде 11.3-6. Это делается просто для описания  в Eq. (11.3-6).Стандартное отклонение , также использует частоту как меру текстуры, т.к к значению стандартного отклонения склоняются интуитивно множество людей. Третий момент
Это мера гладкости на гистограмме пока четвертый момент это мера относительно его значения. Пятый и выше моменты не слишком просты в описании формы гистограммы, но они обеспечивают более количественную дискриминацию текстурного содержания. Некоторые полезные добавочные текстурные меры основываются на гистограммных включениях меры «однородности» представленных в формуле 11.3-8 в Eq. (11.3-6).Стандартное отклонение , также использует частоту как меру текстуры, т.к к значению стандартного отклонения склоняются интуитивно множество людей. Третий момент
Это мера гладкости на гистограмме пока четвертый момент это мера относительно его значения. Пятый и выше моменты не слишком просты в описании формы гистограммы, но они обеспечивают более количественную дискриминацию текстурного содержания. Некоторые полезные добавочные текстурные меры основываются на гистограммных включениях меры «однородности» представленных в формуле 11.3-8
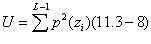 И мера средней энтропии, с которой читатель может ознакомится самостоятельно со справочной литературы или в главе 8 данной книги, в которой энтропия определена как
И мера средней энтропии, с которой читатель может ознакомится самостоятельно со справочной литературы или в главе 8 данной книги, в которой энтропия определена как
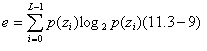 Т.к. имеет значения в диапазоне [0;1] их сумма равна 1, мера U это максимум на изображении в котором все серые уровни равны (максимальная однородность), и уменьшаются там. Энтропия – мера переменчивости и равняется 0 для постоянного изображения.
В таблице 11.2 суммируются значения предыдущих мер для трёх типов текстур, рассмотренных на фигуре 11.22. Только среднее здесь называется средним серым уровнем области и полезен только как грубая идея интенсивности, не как реальная текстура. Стандартное отклонение является долее информативным; значения более чище показаны, чем на первой текстуре, в которой значительно уменьшена переменчивость в сером уровне (это гладкость), чем на остальных двух текстурах. Грубая текстура показана несколько чище в этой мере. Как ожидалось, такие же комментарии накладываются на R, потому что эта мера существенна для такого же предмета как стандартное отклонение. Третий момент преимущественно полезен для определения угла симметрии на гистограмме и относительно них перемещена влево (отрицательные значения) или вправо (положительные значения).
Т.к. имеет значения в диапазоне [0;1] их сумма равна 1, мера U это максимум на изображении в котором все серые уровни равны (максимальная однородность), и уменьшаются там. Энтропия – мера переменчивости и равняется 0 для постоянного изображения.
В таблице 11.2 суммируются значения предыдущих мер для трёх типов текстур, рассмотренных на фигуре 11.22. Только среднее здесь называется средним серым уровнем области и полезен только как грубая идея интенсивности, не как реальная текстура. Стандартное отклонение является долее информативным; значения более чище показаны, чем на первой текстуре, в которой значительно уменьшена переменчивость в сером уровне (это гладкость), чем на остальных двух текстурах. Грубая текстура показана несколько чище в этой мере. Как ожидалось, такие же комментарии накладываются на R, потому что эта мера существенна для такого же предмета как стандартное отклонение. Третий момент преимущественно полезен для определения угла симметрии на гистограмме и относительно них перемещена влево (отрицательные значения) или вправо (положительные значения).
 Это даёт грубую идею относительно серых уровней и показывает смещение в строну темных или светлых значений средних. В терминах текстуры, информация полученная с третьего момента полезна только когда изменения между измерениями достаточно большие. Смотря на меру однородности мы снова заключаем, что первое подизображение более гладко (у него большая однородность, чем у остальных) и наиболее случайно (самая низкая однородность) соответствует грубой текстуре. Это не удивительно. В заключение, значение энтропии находятся в противоположном порядке и таким образом ведут к аналогичным заключениям к которым мы пришли по поводу меры однородности. Первое подизображение имеет самое низкое изменение в сером уровне и в грубом изображении наибольшее. Регулярная текстура находится между двумя экстремумами относительно обоих этих мер.
Меры текстур, вычисленные только на основе гистограмм страдают из-за ограничений того, что они не несут никакой полезной информации относительно позиций пикселей относительно друг друга. Один из способов привнести этот вид этот вид информации в текстурный анализ – процесс рассмотрения не только распределения интенсивности, но также и позиции пикселей с равными или приблизительно равными значениями интенсивности.
Пусть P будет позиция оператора и пусть A будет матрицей k*k, элементы которой - это количество раз, которые точки с серым уровнем проходят (в позиции P) относительно с серым уровнем , с 1<=i, j<=k. Для примера рассмотрим изображение с тремя серыми уровнями =0, =1 и =2, как следующее:
Это даёт грубую идею относительно серых уровней и показывает смещение в строну темных или светлых значений средних. В терминах текстуры, информация полученная с третьего момента полезна только когда изменения между измерениями достаточно большие. Смотря на меру однородности мы снова заключаем, что первое подизображение более гладко (у него большая однородность, чем у остальных) и наиболее случайно (самая низкая однородность) соответствует грубой текстуре. Это не удивительно. В заключение, значение энтропии находятся в противоположном порядке и таким образом ведут к аналогичным заключениям к которым мы пришли по поводу меры однородности. Первое подизображение имеет самое низкое изменение в сером уровне и в грубом изображении наибольшее. Регулярная текстура находится между двумя экстремумами относительно обоих этих мер.
Меры текстур, вычисленные только на основе гистограмм страдают из-за ограничений того, что они не несут никакой полезной информации относительно позиций пикселей относительно друг друга. Один из способов привнести этот вид этот вид информации в текстурный анализ – процесс рассмотрения не только распределения интенсивности, но также и позиции пикселей с равными или приблизительно равными значениями интенсивности.
Пусть P будет позиция оператора и пусть A будет матрицей k*k, элементы которой - это количество раз, которые точки с серым уровнем проходят (в позиции P) относительно с серым уровнем , с 1<=i, j<=k. Для примера рассмотрим изображение с тремя серыми уровнями =0, =1 и =2, как следующее:
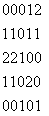 Определим позицию оператора P как «один пиксель вправо и один пиксель вниз», описываемый следующую матрицу 3*3:
Определим позицию оператора P как «один пиксель вправо и один пиксель вниз», описываемый следующую матрицу 3*3:
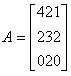 где к примеру (вершина слева) – количество раз, которые точка с уровнем =0 показывает один пиксель, расположенный вниз и вправо от пикселя в таким же серым уровнем, и (вершина справа)- количество раз, которые точка с серым уровнем =2 показывает один пиксель, расположенный вниз и вправо от пикселя в серым уровнем =2. Размер A определяется номером различимых серых уровней во входном изображении. Таким образом концепция дискуссии в этой секции обычно требует, чтобы интенсивность была повторно квантована в несколько полос серого уровня для того, чтобы держать размер А управляемым. ). Более детально, проблема анализа данной матрицы С заключается в порядке категории текстуры области, по которой С была вычислена. Набор описателей, полезный для этой цели, включает в себя следующее:
где к примеру (вершина слева) – количество раз, которые точка с уровнем =0 показывает один пиксель, расположенный вниз и вправо от пикселя в таким же серым уровнем, и (вершина справа)- количество раз, которые точка с серым уровнем =2 показывает один пиксель, расположенный вниз и вправо от пикселя в серым уровнем =2. Размер A определяется номером различимых серых уровней во входном изображении. Таким образом концепция дискуссии в этой секции обычно требует, чтобы интенсивность была повторно квантована в несколько полос серого уровня для того, чтобы держать размер А управляемым. ). Более детально, проблема анализа данной матрицы С заключается в порядке категории текстуры области, по которой С была вычислена. Набор описателей, полезный для этой цели, включает в себя следующее:
-
Максимальная вероятность
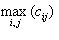
-
Элементы разных моментов порядка k

-
Инвертированные элементы разных моментов порядка k

-
Однородность
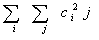
-
Энтропия
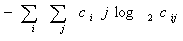
- Основная идея, характеризующая содержимое С включает те дескрипторы. Для примера, первое вероятность дает индикацию силы ответа для Р. Второй дескриптор имеет относительно низкое значение, когда высоки значения матрицы С возле главной диагонали, потому что различия (i-j) малы там. Третий дескриптор имеет противоположный эффект. Четвертый дескриптор самый высокий когда для всех равны. Как было замечено выше, пятый дескриптор, это мера случайности, показывающая свои самые высокие значения, когда все элементы С максимально случайны. Один из методов для использования этих дескрипторов – обучение системы значений дескрипторов для набора разных текстур. Область с неизвестной текстурой будет впоследствии определена в зависимости от того, насколько близко ее дескрипторы соответствуют дескрипторам сохраненным в памяти. Мы обсудим соответствие более детально в Главе 12.
© ДонНТУ 2008г. Кривопуск Т.И.
|


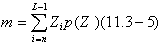
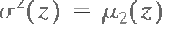 )особенно важен в описании текстуры. Это мера контрастного серого уровня, которая может быть использована для установления описателей относительно гладкости. Для примера, мера
)особенно важен в описании текстуры. Это мера контрастного серого уровня, которая может быть использована для установления описателей относительно гладкости. Для примера, мера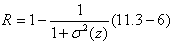
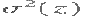 Т.к. значение выражения склоняется к большой серой шкале изображений со значениями, например, в диапозоне от 0 до 255, это хорошая идея для нормализации выражения в интервале [0,1] используемой в формуде 11.3-6. Это делается просто для описания
Т.к. значение выражения склоняется к большой серой шкале изображений со значениями, например, в диапозоне от 0 до 255, это хорошая идея для нормализации выражения в интервале [0,1] используемой в формуде 11.3-6. Это делается просто для описания  в Eq. (11.3-6).Стандартное отклонение , также использует частоту как меру текстуры, т.к к значению стандартного отклонения склоняются интуитивно множество людей. Третий момент
в Eq. (11.3-6).Стандартное отклонение , также использует частоту как меру текстуры, т.к к значению стандартного отклонения склоняются интуитивно множество людей. Третий момент