Измерение коэффициента затухания и фазовой постоянной распространения в микрополосковом преобразователе поверхностных магнитостатических волн в диапазоне 9-9.8 GHz
© М.А. Григорьев, А.П. Гей, А.И. Мищенко, Ю.Н. Навроцкая, А.В. Толстиков
Саратовский государственный университет, 410071 Саратов, Россия
Журнал технической физики, 1998, том 68, № 12
(Поступила в редакцию 15 октября 1996 г. В окончательной редакции 3 июля 1997 г.)
Оригинал статьи: http://www.ioffe.ru/journals/jtf/1998/12/p68-74.pdf
Экспериментально исследовался разомкнутый на конце микрополосковый преобразователь, возбуждающий поверхностную магнитостатическую волну в диапазоне частот 9-9.8 GHz при различных магнитных полях. Описана методика измерения в СВЧ входного импеданса преобразователя при наличии между ним и измерителем сопротивления набора соединительных волноводных элементов с потерями. Получены зависимости коэффициента излучения и фазовой постоянной распространения электромагнитной волны в преобразователе от индукции магнитного поля. Вычислены коэффициенты преобразования электромагнитной энергии в поверхностную магнитостатическую волну.
Введение
Для возбуждения и приема магнитостатических волн (МСВ) обычно используется микрополосковый преобразователь (МП). Он представляет собой отрезок узкой металлической полоски, нанесенной либо на поверхность ферритовой пленки (ФП), в которой возбуждается МСВ, либо на диэлектрическую подложку, прижимаемую к ФП. Вместе с заземленным основанием эта полоска образует короткую двухпроводную линию, один из концов которой соединен с источником электромагнитной (ЭМ) мощности. Обычно длина полоски выбирается малой по сравнению с длиной ЭМ волны в такой линии, и тогда другой конец должен быть закорочен (режим КЗ). Если же его оставить разомкнутым (режим "холостого хода" — ХХ), то переменный ток, текущий по полоске, будет практически равен нулю и она не сможет возбуждать МСВ.
Настоящая работа посвящена исследованию МП, возбуждающего на частотах около 10 GHz поверхностные магнитостатические волны ПМСВ в касательно намагниченной ФП при условии, что протяженность полоски превышает длину ЭМ волны. Подобная ситуация имеет место, например, при реализации на указанных частотах магнитооптического взаимодействия, эффективность которого растет с увеличением длины МП.
В случае бесконечно длинного МП бегущая в нем ЭМ волна возбуждала бы в ФП независимо от направления намагниченности распространяющиеся в обе стороны от полоски магнитостатические волны с линейными фронтами и волновыми векторами, модули которых равны KMSW = ω/VMSV, где ω — частота, VMSW — скорости тех типов МСВ, которые при этом возбуждаются. Проекции волновых векторов этих волн на направление МП должны быть равны волновому числу ЭМ волны вМП KEM = ω/ VEM, где VEM — скорость ЭМ волны. Отсюда следует, что волновые вектора возбуждаемых МСВ в плоскости параллельной ФП должны составлять с нормалью к полоске углы θ = arcsin(VMSW/VEM).
Если же МП имеет конечную длину, то в нем независимо от режима КЗ или ХХ установится стоячая ЭМ волна, представляющая собой сумму прямой и отраженной бегущих волн. Каждую из них можно рассматривать как источник возбуждения парциальных МСВ. Последние в связи с дифракционной расходимостью будут иметь квазилинейные фронты и характеризоваться некоторыми угловыми спектрами. Однако и в этом случае направления главных лепестков указанных спектров составят углы ± θ с нормалью к полоске. Знаки "+"и"-" относятся соответственно к прямой и обратной ЭМ волнам.
В случае касательно намагниченной ФП, когда будут возбуждаться только ПМСВ, прямая и обратная ЭМ волны, образующие стоячую волну в МП, создадут две пары парциальных ПМСВ. Первая из них распространяется по одну сторону от плоскости симметрии преобразователя, а вторая — по другую.
При распространении вдоль МП ЭМ волна испытывает затухание не только за счет диссипации в металлических проводниках и диэлектрике, но и за счет возбуждения ПМСВ. Можно считать, что возбуждение ПМСВ эквивалентно внесению в линию некоторого дополнительного погонного комплексного сопротивления, которое будем называть импедансом излучения Zrad = Rrad + jXrad. Диссипация в линии может иметь место как за счет конечного омического сопротивления проводов, так и за счет активной проводимости среды, заполняющей линию. Если принять, что указанная проводимость потерь пренебрежимо мала, то диссипация будет определяться только погонным активным сопротивлением проводов Rlos. Тогда доля от подводимой ЭМ мощности, приходящаяся на возбуждение всех ПМСВ, составит Rrad/(Rrad + Rlos), а остальная часть перейдет в тепло.
В связи с затуханием ЭМ волны амплитуда возбуждаемой МСВ не остается постоянной по сечению пучка. Она будет спадать вдоль МП. При этом ПМСВ, происходящая от прямой ЭМ волны, очевидно, будет иметь большую амплитуду, чем от обратной. Поэтому МП должен быть так сориентирован на поверхности ФП, чтобы более интенсивная парциальная ПМСВ распространялась бы в нужном направлении, а направление касательной намагниченности ФП было бы выбрано так, чтобы возбуждением других типов МСВ можно было пренебречь. Следует также иметь в виду, что в ближней зоне, где перекрываются пучки, порожденные прямой и обратной ЭМ волнами, наблюдается сложная интерференционная картина распределения амплитуды колебаний. Очевидно, на достаточном удалении от МП каждую из парциальных ПМСВ можно принять приемной антенной, если ее правильно расположить на поверхности ФП. Однако и в ближней зоне их реально нетрудно обнаружить (разделить), например, с помощью магнитооптического взаимодействия, поскольку для получения дифрагированного света падающий лазерный пучок необходимо направить к фронту МСВ под определенным углом, известным как угол Брегга.
Все возбуждаемые волны в совокупности обладают суммарной мощностью
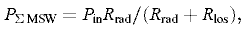
где Pin — ЭМ мощность, введенная в МП.
В волноводе, подводящем энергию от генератора к МП, установится стоячая волна, образованная прямой и отраженной ЭМ волнами, переносящими соответственно мощности P+ иР— Последняя из них определяется коэффициентом отражения г, который в свою очередь зависит от входного импеданса Zin = Rin + jXin преобразователя.
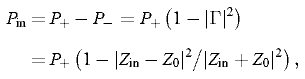
где Z0 — волновое сопротивление волновода.
Если ввести суммарный коэффициент преобразования ηΣ = PΣ MSW/P+, то будем иметь
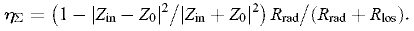(1)
Мощность более интенсивной парциальной ПМСВ PMSW+ составляет менее половины от мощности, затраченной на возбуждение всех четырех волн. Следовательно, коэффициент преобразования для используемой парциальной волны η = PMSW+/P+ не может превысить η Σ /2. Если допустить, что обе парциальные ПМСВ, возбуждаемые прямой ЭМ волной, имеют одинаковую мощность, то можно получить
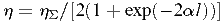, (2)
где α — коэффициент затухания ЭМ волны в МП, обусловленный совместным действием диссипации и преобразования; l — длина МП.
Пренебрегая в МП шунтирующей проводимостью потерь и считая, что диссипация определяется только погонным сопротивлением Rlos, можно показать [1],что если (Rrad + Rlos)2/4 β 2Z02MS << 1, где β — фазовая постоянная распространения ЭМ волны в МП: Z0MS — волновое сопротивление МП, рассчитанное без учета затухания, то коэффициент a связан с погонным сопротивлением (Rrad + Rlos) выражением
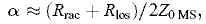, (3)
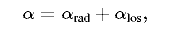, (4)
где α rad = Rrad/2Z0MS будем называть коэффициентом излучения, а alos = Rlos / 2Z0MS — коэффициентом потерь.
Следует отметить, что для преобразователей, длина которых сравнима или превышает длину ЭМ волны, логичнее характеризовать эффективность не сопротивлением излучения Rrad, а коэффициентом излучения α rad. Тогда формула (1) примет вид
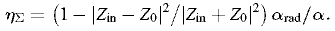, (5)
Известно [1], что входное сопротивление Zin линии с потерями, находящейся в состоянии КЗ или ХХ, выражается формулой
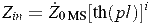, (6)
где p = α + j β, i = 1 для КЗ, i = -1 для ХХ, ZZ0MS — комплексное волновое сопротивление МП;
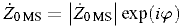, (7)
где при Glos = 0
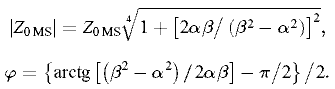
Формулы (5)-(7) позволяют вычислить коэффициент преобразования и, таким образом, найти долю, которую составляет мощность возбужденной МСВ от мощности прямой ЭМ волны в подводящем волноводе. Для этого необходимо знать комплексную постоянную распространения p, а также коэффициенты излучения и потерь — α rad и α los.
Настоящая работа посвящена нахождению значений a, в и arad по результатам измерения входного импеданса МП в случае возбуждения поверхностной магнитоста-тической волны (ПМСВ). Эксперименты выполнялись на частотах 9.0, 9.4, 9.8 GHz при различных магнитных полях.
Нам известны четыре публикации [2-5],в которых для короткозамкнутых МП приводятся результаты измерений импеданса излучения на частотах 1-5 GHz. В двух из них исследовались короткие МП, длина которых была существенно меньше длины ЭМ волны. В [4] изучались МП различной длины от 4 до 16 mm. Однако и здесь размеры преобразователя, выраженные в длинах ЭМ волн, изменялись в интервале от 0.075 до 0.6. В работе [5] исследовались МП длиной 1, 2 и 4 mm в диапазоне 4-5 GHz, что в длинах волн составляло 0.05 - 0.2. В [2-4] измерения выполнялись с помощью промышленных измерителей комплексных коэффициентов передачи и вопрос об учете влияния набора элементов передающего тракта, неизбежно присутствующих в экспериментальной установке не рассматривался. В [5] с целью устранения влияния переходных трактов была изготовлена специальная микрополосковая измерительная линия с подвижным петлевым зондом, непосредственно питающая МП. С ее помощью измерялось входное сопротивление замкнутого на конце МП и по полученным результатам вычисля искомый импеданс излучения.
Следует отметить, что изготовление специальной измерительной линии с целью измерения входного импеданса МП является трудной задачей. Дело в том, что для перемещения зонда необходимо создание механизма, работающего в непосредственной близости от зазора электромагнита, где еще ощутимо довольно сильное магнитное поле. К тому же требуется обеспечивать весьма точное измерение перемещений зонда. Чтобы проиллюстрировать последнее утверждение приведем следующий пример. На частоте 5 GHz длина волны в микрополосковой линии на поликоре равна 2 cm. При длине МП 4 mm фаза коэффициента отражения на входе в МП близка к 0.2 π. В таком случае ошибка в отсчете положения зонда, равная ≈ 0.1 mm, дает относительную погрешность измерения фазы ≈ 20%.
В отличие от упомянутых работ мы проводили эксперименты с МП, работавшим в режиме ХХ и на более высоких частотах (9-9.8 GHz) при длине исследовавшегося преобразователя 13.5 mm, что составило 1.1-1.2 Λ (Λ — длина волны в волноводе). В качестве измерительного прибора использовалась стандартная волноводная измерительная линия (ИЛ). В связи с последним обстоятельством мы значительное место уделили методике измерений, обеспечивающей учет переходного трансформатора импедансов с потерями. Следует также отметить, что мы измеряли более естественную для преобразователей бегущей волны величину — комплексную постоянную распространения α + j β, а не погонный импеданс излучения. И наконец, в отличие от других авторов по результатам своих экспериментов мы выполнили оценки коэффициентов преобразования электромагнитной энергии в энергию возбуждаемой поверхностной МСВ.
Отметим также, что экспериментальные результаты здесь не сопоставляются с теорией. Дело в том, что в существующих теоретических работах отыскивался импеданс излучения для коротких МП [2,6,7], когда ЭМ поле вдоль преобразователя не изменяется. В работе [8] получены лишь уравнения для нахождения комплексных постоянной распространения α + j β и характеристического импеданса, но нет их численного анализа. Нахождение теоретических значений указанных величин потребовало бы от нас значительной вычислительной работы, что не входило в нашу задачу.
Исследуемый преобразователь
ПМСВ возбуждалась в пленке железо-иттриевого граната (ЖИГ), выращенной на подложке из галлий гадо-линиевого граната (ГГГ). Последняя была параллельна плоскости (111) и имела толщину h = 0.5 mm, а нанесенные на ее поверхности слои ЖИГ по 1.56 yum. Исследуемый МП представлял собой медную полоску, напыленную в вакууме непосредственно на пленку ЖИГ, длиной l = 13.5mm, шириной w = 50 μ m и толщиной 2-3 μ m. Вся структура располагалась на заземленном латунном основании, к которому был прикреплен коаксиально-полосковый переход с волновым сопротивлением 50 ??. Полоска совместно с основанием образовывала отрезок высокоомной микрополосковой линии, разомкнутой на одном конце и соединенной с подводящим трактом на другом. Оконечным участком этого тракта, непосредственно соединенным с МП, служила микрополосковая линия с волновым сопротивлением 50 Ω.Она была образована на той же структуре ЖИГ-ГГГ-ЖИГ медной полоской шириной 0.5 mm, длиной 5 mm, расположенной перпендикулярно исследуемому МП. Конструкция в целом помещалась в зазор электромагнита, создающего постоянное магнитной поле, направленное параллельно МП. При такой его ориентации в слое ЖИГ возбуждалась ПМСВ [9].
Методика измерений
ЭМ мощность подводилась к исследуемому МП следующими элементами передающего тракта: прямоугольным волноводом (23 x 10 mm), волноводно-коаксиальным и коаксиально-полосковым переходами, отрезком жесткой коаксиальной линии (Z0 = 50 Ω) и отрезком микрополосковой линии (Z0 = 50 Ω, l = 5mm).Перечисленные элементы в совокупности представляли собой четырехполюсник, входные "клеммы" которого (aa) находились в некотором сечении прямоугольного волновода, а выходные (bb) — в месте соединения МП с микрополосковой линией. Суть применявшегося метода, называемого обычно методом четырехполюсника, заключалась в измерении с помощью ИЛ импеданса на клеммах (aa) и последующем вычислении искомого импеданса на клеммах (bb). Чтобы такое вычисление стало возможным необходимо в первую очередь найти параметры четырехполюсника, расположенного между указанными клеммами.
Известно [10], что любой пассивный четырехполюсник трансформирует сопротивление по закону
, (8)
где A, B, C, D — комплексные элементы матрицы передачи (A-параметры).
Последние можно найти, если провести вспомогательные эксперименты, заключающиеся в измерении Zin при подключении к выходу известных сопротивлений (эталонов) Zet. Трех таких экспериментов достаточно, чтобы найти приведенные А-параметры A/D = a, B/D = b, C/D = c, полностью определяющие закон трансформации сопротивления.
В нашем случае технические трудности не позволяли подключать эталоны непосредственно к выходу четырехполюсника. Поэтому был образован вспомогательный (новый) четырехполюсник, который на выходе заканчивался стандартным коаксиальным соединителем. Последний обеспечивал подключение к выходу в качестве эталонов отрезка коаксиальной линии с подвижным поршнем (эталон реактансов). Импедансы таких эталонов при различных положениях поршня предварительно измерялись с помощью коаксиальной ИЛ. Новый четырехполюсник был образован заменой микрополосковой линии с коаксиально-полосковым переходом отрезком коаксиальной линии со стандартным соединителем на выходе. Таким образом, экспериментально находились параметры a, b, c нового четырехполюсника, а при последующем вычислении искомого импеданса преобразователя указанная замена учитывалась расчетным путем. При этом к новому четырехполюснику как бы подключались последовательно еще два дополнительных четырехполюсника, учитывающих возврат к исходному состоянию. Первый из них учитывал удаление отрезка коаксиальной линии, а второй — возвращение микро-полосковой линии. Закон трансформации сопротивления использовался в виде
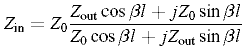, (9)
где β — фазовая постоянная распространения, l — длина линии.
Первый отрезок рассматривался как линия отрицательной длины с волновым сопротивлением 50 Ω,а второй — как линия положительной длины (l = 5mm) с рассчитанными [11] волновым сопротивлением и длиной волны Λ = λ / ∞ ε ef, где ε ef — эффективная диэлектрическая проницаемость. При этом считалось, что диэлектриком в линии является ГГГ с относительной диэлектрической проницаемостью ε r = 14. Длина первого дополнительного участка находилась экспериментально как длина стандартной линии, обеспечивающей тот же сдвиг фазы, что и реальная. С этой целью ИЛ закорачивалась короткозамыкателем и находился минимум стоячей волны. Затем к ИЛ подключался исследуемый переход, закороченный на выходе, и находилось смещение минимума, которое принималось за эквивалентную длину. Короткое замыкание исследуемого перехода создавалось тонкой медной шайбой, вставлявшейся в разъем в плоскости, совпадающей с началом микрополосковой линии.
Нахождение A-параметров
Прежде всего измерялись импедансы эталонов. Для этого использовалась установка, состоящая из генератора сигналов, работавшего в режиме импульсной модуляции с частотой повторения 1 KHz и скважностью 2, ферритового вентиля, поляризационного аттенюатора и коаксиальной ИЛ. К детектору последней был подключен селективный микровольтметр. К выходу ИЛ подсоединялись исследуемые эталоны. Сначала ИЛ нагружалась короткозамыкателем КЗ и находился минимум стоячей волны. Найденное положение минимума, как известно, является плоскостью эквивалентной КЗ. Затем вместо КЗ к ИЛ присоединялся эталон реактансов, и при трех положениях его поршня измерялись импедансы в найденной эквивалентной плоскости. Коэффициент стоячей волны (КСВ) измерялся методом калиброванного аттенюатора [12], а координата эквивалентной плоскости d находилась как расстояние от ближайшего (со стороны генератора) минимума. Искомый импеданс вычислялся по измеренным величинам КСВ и d [12]. Таким образом, для трех частот (9.0, 9.4, 9.8 GHz) были получены по три импеданса эталонов Zet, i = Ret, i + jXet, i, i = 1,2,3. Затем в измерительной установке коаксиальная ИЛ заменялась на волноводную. Последняя нагружалась "новым" четырехполюсником, к выходу которого подключался эталон реактансов. Измерения импеданса выполнялись в плоскости, эквивалентной фланцу ИЛ. Она находилась как положение минимума при КЗ на указанном фланце. Для заданной частоты это место принималось за клеммы aa. Полученные значения КСВ и координаты d использовались затем для вычисления активного и реактивного сопротивления на входе четырехполюсника, т. е. Rin, i и Xin, i. При этом постоянная распространения вычислялась по измеренной длине волны в волноводе β = 2 π/Λ, а волновое сопротивление — по формуле Z0 = 240 π (b'/а') (Λ / λ)[12],где a' и b' — размеры широкой и узкой стенок волновода соответственно, Λ — длина волны в свободном пространстве. В результате для каждой частоты были получены по три значения импеданса на входе исследуемого четырехполюсника Zin, i = Rin, i + jXin, i, i = 1,2,3. Искомые Λ -параметры a = a1 + ja2, b = b1 + jb2, c = c1 + jc2 находились как решение системы трех пар линейных алгебраических уравнений вида
&#nbsp (10)
(i = 1,2,3), полученных в результате подстановкиZin, i и Zet, i (8).
Для каждой частоты при решении системы (10) были найдены по три комплексных значения А-параметров.
Измерение входного импеданса МП
После восстановления четырехполюсника в исходное состояние были измерены импедансы на клеммах aa с помощью волноводной ИЛ. Эксперименты выполнялись при четырех значениях индукции магнитного поля B, равных 0.136, 0.198, 0.233, 0.308 T. По полученным результатам и формулам (8) и (9) были вычислены импедансы на клеммах bb, т. е. на входе исследуемого МП. На рис. 1 показаны экспериментальные зависимости активного (а) и реактивного (b) входных сопротивлений МП Rin и Xin от величины B при постоянных значениях частот. Величины Rin и Xin при изменении B испытывают заметные колебания. Активное сопротивление Rin проходит через максимум, достигая наибольшего значения при различных магнитных полях в зависимости от частоты. При f = 9 GHz максимум Rin и 13 Ω имеет место при β ≈ 0.18 T. С увеличением частоты этот максимум перемещается в сторону больших значений B, одновременно спадая по величине. На частотах 9.4, 9.8 GHz он соответственно равен 57 и 40 Ω. Очевидно, величина Rin зависит от сопротивления излучения и ее спад означает уменьшение мощности возбуждаемой ПМСВ.
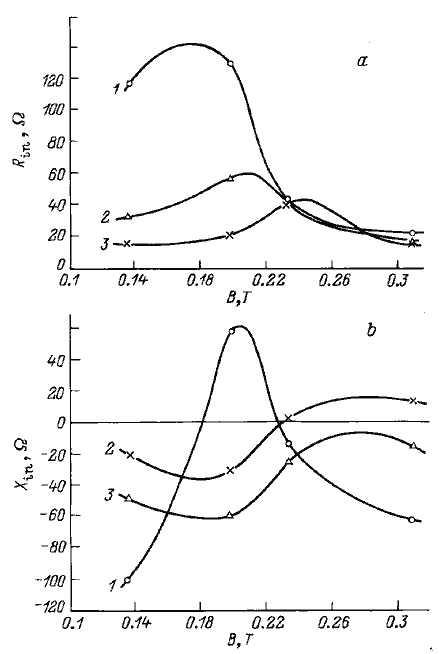
Рис. 1. Зависимости величины составляющих входного импеданса разомкнутого на конце микрополоскового преобразователя ПМСВ длиной 13.5 mm от индукции магнитного поля. Частота, GHz: 1 —9.0, 2 — 9.4, 3 — 9.8.
Минимальное значение Rin и 16 Ω получено при B = 0. 308 T на частоте 9.8 GHz. Можно предположить, что при этом МП практически не возбуждает ПМСВ, а измеренная величина Rin обусловлена диссипацией, вызванной главным образом омическим сопротивлением его проводов. Изменение реактивной составляющей входного импеданса Xin может быть связано как с изменением погонного сопротивления излучения, так и с изменением фазовой постоянной распространения в ЭМ волны в МП. Наибольшие колебания Xin в зависимости от B наблюдаются на частоте 9 GHz, где и Rin испытывает наиболее сильные изменения.
Следует заметить, что приведенные экспериментальные результаты уже сами по себе представляют ценную информацию о величине входного импеданса длинного разомкнутого МП и его зависимости от магнитного поля и частоты. Они необходимы при решении задачи о согласовании МП с передающим трактом.
Мы воспользовались полученными результатами, чтобы в случае преобразователя с бегущими ЭМ волнами выяснить, как ведут себя коэффициент затухания α = αrad + αlos и фазовая постоянная распространения в этих волн для выбранных частот и магнитных полей.
Нахождение коэффициента затухания и постоянной распространения
В пренебрежении шунтирующей проводимостью потерь комплексное волновое сопротивление микропо-лосковой линии, входящее в (6), можно выразить через α и β следующим образом [1]:
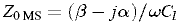, (11)
где C1 — погонная емкость МП, определяемая геометрическими размерами МП и эффективной диэлектрической проницаемостью среды, на которой образована микропо-лосковая линия.
Если пренебречь влиянием ферритовых пленок, то такой средой в нашем случае является пластина ГГГ. Подставляя формулу (11) в (6), будем иметь
,
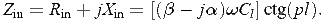Если ввести обозначение ctg[( α + j β )l]= ξ + j ψ, то нетрудно получить в форме удобной для численного решения следующую систему уравнений:
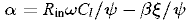, (12)
, (13)
,
В указанных формулах кроме измеренных значений Rin и Xin задавались длина МП l = 13.5 mm и погонная емкость C, 1 которая находилась из (11) при α = 0 какC1 = √ ε ef/cZ0MS, где с — скорость света в вакууме. Значения ε ef и Z 0, MS вычислялись по формулам, взятым из [ 11 ] для микрополосковой линии с полоской нулевой толщины и с w/h < 1
,
В результате применения этих формул были получены численные значения величин ε ef; Z0MS, Ω ; C1, 10-10, F/m соответственно для 9.0GHz 8.407, 91.56, 1.056, для 9.4 GHz 8.429, 91.56, 1.058, для 9.8 GHz 8.452, 91.56, 1.059.
При нахождении α и β из множества возможных решений системы уравнений (12) и (13) выбиралось то, для которого постоянная распространения β была наиболее близка к значению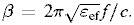 
Полученные зависимости представлены на рис. 2.
Обсуждение полученных результатов
Обращает на себя внимание внешнее сходство зависимостей α (B) и Rin(B), а также β (B) и Xin(B).Сходство первых их них физически понятно, поскольку наличие затухания в разомкнутой или замкнутой линии ведет к появлению на ее входе активного сопротивления. Что касается реактивной составляющей Xin и фазовой постоянной β, то отмеченное выше сходство определяется математической связью между ними. Величина в входят в аргумент функции (6), мнимая часть которой приближенно описывается формулой Xin ≈ – ctg(β l). Последняя в небольшом интервале β l может быть аппроксимирована линейной зависимостью. Это и приводит к сходству кривых β (B) и Xin(B).
Значения α для максимумов кривых на рис. 2, а можно интерпретировать следующим образом. При распространении ЭМ волны вдоль МП переносимая ею мощность уменьшается за счет потерь и возбуждения ПМСВ. На каждый сантиметр длины МП на частотах 9.0, 9.4, 9.8 GHz это уменьшение составляет в 2.3, 1.9, 1.6 раз соответственно.
По формулам (1) и (2) нетрудно вычислить коэффициенты преобразования ηΣ и η. Если считать, что МП является нагрузкой передающей линии с волновым сопротивлением Z0 = 50 Ω, а коэффициенты αlos равны минимальным значением а на кривых рис. 2, а,то получим результаты, сведенные в таблицу.
Интересно прежде всего сопоставить полученные значения αrad с результатами других авторов.
Наиболее близкой нам по частоте и методике эксперимента является работа [5]. Пересчет наших величин α rad, приведенных в таблице, в значения Rrad с целью сравнения с указанной работой дал для частот 9.0, 9.4, 9.8 GHz соответственно 5.3, 3.8, 3.1 Ω /mm. Сопротивление излучения из [5] для случая возбуждения ПМСВ в касательно намагниченной ФП близки нашим по порядку величины и характеру зависимости от частоты (при f = 4.1 ... 5 GHz Rrad = 20 ... 4 Ω /mm). Точного совпадения не следует ожидать, поскольку в нашем случае частота была почти вдвое больше, а пленка ЖИГ в 3 раза толще.
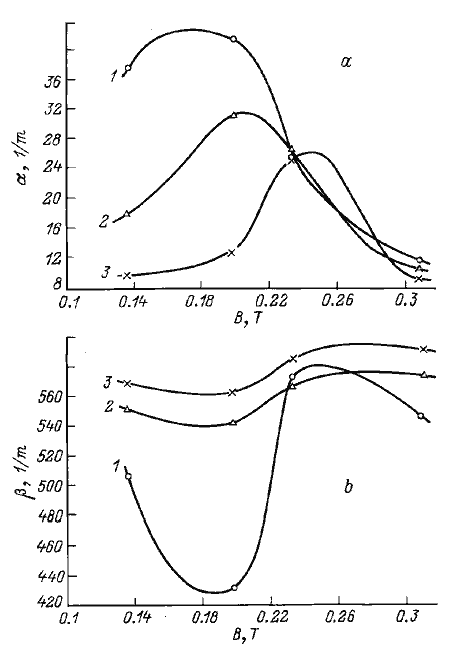
Рис. 2. Зависимости коэффициента затухания (а) и фазовой постоянной распространения (b) электромагнитной волны в микрополосковом преобразователе ПМСВ от индукции магнитного поля (1-3 — то же, что и на рис. 1).
Из таблицы следует, что, хотя а при изменении частоты меняется, коэффициент η для используемой парциальной ПМСВ остается практически постоянным. Приведенные значения η Σ означают, что на все четыре парциальные ПМСВ приходится 56-63% от проводимой ЭМ мощности. При этом в используемую парциальную ПМСВ преобразуется лишь 17.4-21.4%. Отметим, что интенсивность возбужденной ПМСВ меняется вдоль МП в 1.6-2.3 раза.
Известно, что когда передающая линия нагружена некоторым комплексным сопротивлением, то мощность, потребляемая нагрузкой, достигает максимума, если волновое сопротивление линии выбрано оптимальным, а сама линия согласована с генератором. Оптимальное значение Z0 равно модулю импеданса нагрузки. Приведенные в таблице коэффициенты ηΣ и η рассчитаны для постоянного Z0. Последняя величина наиболее сильно отличается от оптимального значения на частоте 9.0 GHz. В таблице приведены оптимальные волновые сопротивления Z0, opt и соответствующие коэффициенты преобразования η opt. Легко видеть, что использование оптимальных волновых сопротивлений могло бы дать заметное увеличение η лишь на частоте 9.0 GHz.
Остановимся теперь на поведении фазовой постоянной распространения β. Из экспериментальных кривых, приведенных на рис. 2,b, следует, что в испытывает колебания при изменении магнитного поля. Амплитуда этих колебаний невелика и составляет на частотах 9.4 и 9.8 GHz 3% от средней величины, а на частоте 9.0 GHz достигает 15%. При этом рост α сопровождается падением β. Это означает, что возбуждение ПМСВ приводит к увеличению фазовой скорости ЭМ волны в МП. Известно [1] , что в случае, когда затуханием в линии можно пренебречь, фазовая скорость связана с погонными параметрами L1 и Сrad формулой νƒ = 1/ √ L1C1. Можно предположить, что увеличение фазовой скорости вызывается уменьшением погонной индуктивности при возбуждении ПМСВ.
Заключение
В ходе экспериментов была разработана методика СВЧ измерений входного импеданса микрополоскового преобразователя ПМСВ, позволяющая учесть влияние трансформатора сопротивлений, образованного элементами передающего тракта. По результатам применения этой методики в коротковолновой части СВЧ диапазона впервые получены экспериментальные зависимости коэффициента затухания и фазовой постоянной распространения в длинном, разомкнутом на конце микропо-лосковом преобразователе ПМСВ от индукции магнитного поля, а также вычислены коэффициенты преобразования. Полученные зависимости могут быть использованы для проверки теории, а также при разработке эффективных преобразователей ПМСВ.
Список литературы
1. Калинин В.И., Герштейн Г.М. Введение в радиофизику.М.: Гиз. Тех.-Теор. Лит., 1957. 660 с.
2. Ganguly A.K., Webb D.C. // IEE Trans. MTT. 1975. Vol. 23. N 12. P. 998-1006.
3. Ganguly A.K., Webb D.C., Banks C. // IEE Trans. MTT. 1978. Vol. 26. N 6. P. 444-447.
4. Сорокин В.Г., Богун П.В., Кандыба П.Е. // ЖТФ. 1986. Т. 56. Вып. 12. С. 2377-2382.
5. Дмитриев В.Ф., Калиникос Б.А., Ковшиков Н.Г. // ЖТФ. 1986. Т. 56. Вып. 11. С. 2169-2177.
6. Emtage P.R. // J. Appl. Phys. 1978. Vol. 49. N 8. P. 4475-4484.
7. Вугальтер Г.А., Малахин В.Н. // ЖТФ. 1985. Т. 55. Вып. 3. С. 497-506.
8. Гилинский И.А., Щеглов И.М. Препринт ИФП СО АН СССР. № 3-84. Новосибирск. 1984. 21 с.
9. Вашковский А.В., Стальмахов В.С., Шараевский Ю.П. Магнитостатические волны в электронике сверхвысоких частот. Из-во СГУ, 1993. 311 с.
10. Шимони К. Теоретическая электроника. М.: Мир, 1964. 760 с.
11. Справочник по расчету и конструированию СВЧ полоско-вых устройств / Под ред. В.И. Вольмана. М.: Радио и связь, 1982. 328 с.
12. Гинзтон Э.Л. Измерения на сантиметровых волнах. М.: ИЛ, 1960. 620 с.
