Автор: Сергей Бузыканов
Источник: http://www.soel.ru/cms/f/?/311534.pdf
Определение положения объекта относительно плоскости Земли является важной задачей во многих технических приложениях. Используя ускорение свободного падения, обусловленное наличием гравитационного поля Земли, датчик наклона на основе твердотельного акселерометра позволяет определить угол относительно плоскости Земли с точностью до 0,5 градуса. В данной статье рассматривается задача построения такого датчика, а также некоторые аспекты его применения.
Датчик наклона используется человечеством уже тысячи лет. Самым элементарным приспособлением для этого можно считать отвес, т.е. груз, привязанный к нити. С помощью такого датчика возводились постройки ещё тысячи лет назад. Более сложным и точным устройством является уровень – ёмкость с жидкостью (обычно водой), в которой плавает пузырёк воздуха. Всевозможные приспособления такого типа, позволяющие выровнять уровень относительно Земли, находят широкое применение и сегодня. Однако в ряде случаев необходимо не просто выровнять объект, а знать численное значение угла его наклона относительно Земли, для чего существуют механические угломеры различной конструкции, в основе которых лежит использование силы земного притяжения. Электронные угломеры имеют массу преимуществ перед традиционными механическими устройствами: прямой интерфейс с цифровой системой позиционирования, более точные показания, большая разрешающая способность и т.д. К сожалению, представленные сегодня на рынке электронных приборов цифровые датчики угла имеют относительно высокую цену (от $300). В данной статье рассматривается задача самостоятельного изготовления простого в настройке датчика наклона на основе акселерометра фирмы Analog Device, содержащего минимум деталей и обеспечивающего точность измерения 0,5 градуса.

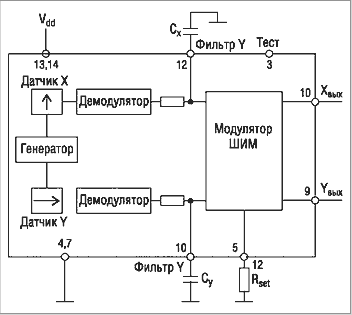
Рисунок 1 - Структурная схема ADXL202
Существует много типов датчиков угла наклона: жидкостные, твердотельные, на основе гироскопного эффекта и т.д. Для многих современных систем позиционирования применяются гироскопы, которые представляют собой датчики с вращающимся рабочим телом большой массы, позволяющим избежать влияния переменного ускорения объекта на результаты измерения. Однако такие датчики обладают рядом существенных недостатков, основным из которых является их высокая стоимость. Другими существенными недостатками таких датчиков является медленная прецессия осей вращения и необходимость регулярной калибровки в течение срока эксплуатации.
Современное развитие микромеханики позволило сконструировать миниатюрные твердотельные датчики ускорения, которые по своим рабочим характеристикам идентичны жидкостным датчикам, но при этом обладают рядом преимуществ: ударо- и вибростойкостью, широким диапазоном рабочих температур, миниатюрностью и.т.д.
При разработке новых устройств важными требованиями является минимизация цены изделия, количества применяемых деталей и скорости разработки. Поэтому для построения датчика угла наклона предлагается использовать акселерометр ADXL202 производства фирмы Analog Device.
Данная микросхема интегрирует в своём составе два аналоговых датчика ускорения (по осям X и Y) и встроенный контроллер обработки, преобразующий аналоговые сигналы датчиков в ШИМ-колебание. Структурная схема ADXL202 приведена на рис. 1.
Датчики ускорения представляют собой набор дифференциальных конденсаторов, образуемых неподвижным основанием и укреплённой на нём с помощью полисиликоновой пружины подвижной части [1, 2]. При приложении внешней силы подвижная часть перемещается относительно неподвижной, соответственно изменяя ёмкость конденсаторов. Сигнал с датчика подаётся на контроллер обработки, который преобразует его в сигнал с ШИМ (рис. 2). Отношение Т1/Т2 прямо пропорционально ускорению, действующему на микросхему.

Рисунок 2 - Сигнал с датчика
Интеграция всех необходимых элементов в одном корпусе позволяет создавать дешёвые, быстро настраиваемые датчики с минимумом дополнительных деталей. Предлагаемая принципиальная схема датчика приведена на рис. 3.
ШИМ-сигналы с обоих датчиков подаются на входы контроллера, который вычисляет отношение Т1/Т2. Для определения ускорения применяется выражение:
A = ( Т1/Т2 - Тoff ) / S
где Toff = Т1/Т2 при нулевом наклоне (ускорении), S – коэффициент шкалы (в среднем S = 12,5%).
Резистором R1 устанавливается период T2 следования импульсов согласно выражению:
T2[с] = R1[Ом] / ( 125 × 106 )
Так, при R1 = 125 кОм получаем частоту следования 1 кГц, т.е. T2 = 1 мс. Акселерометр рассчитан на работу при T2, лежащем в интервале 0,5...10 мс. Величина периода T2 медленно изменяется в зависимости от температуры, поэтому её измерение можно проводить раз в 10...15 мин. При конструировании датчика резистор R1 необходимо располагать как можно ближе к микросхеме для минимизации паразитной ёмкости на этом выводе.

Рисунок 3 - Принципиальная схема датчика угла наклона
Для снижения уровня шума в ADXL202 применяется низкочастотный фильтр. Полоса пропускания данного фильтра на уровне –3 дБ определяется значением ёмкости внешних конденсаторов Cx и Cy согласно формуле:
F–3 дБ = 1 / ( 2π (32 кОм) Cx,y )
или, более просто, F–3 дБ [Гц] = 5 × 10–6/Cx,y [мкФ]. Реальное значение сопротивления внутреннего резистора может изменяться в пределах 32 кОм ± 25%, что, соответственно, изменяет и частоту пропускания. В любом случае ёмкость внешнего конденсатора не должна быть ниже 1000 пФ.
Вычисленное значение угла наклона по интерфейсу RS485 передаётся на цифровую систему позиционирования. Для внутрисхемного программирования микроконтроллера используется SPI-интерфейс, подключаемый через специально введённый разъём.
Угол наклона датчика пропорционален ускорению, действующему на его подвижную часть, и вычисляется по формуле:
φ = arcsin(A)
При микроконтроллерной реализации данного алгоритма для вычисления угла наклона необходимо использовать разложение функции arcsin(А) в ряд Тейлора:
arcsin(А) = A + A3/6 + 3A5/40 + 5A7/112 + 35A9/1152 +...
φ выражается в радианах. Можно показать, что для вычисления угла наклона с точностью до 0,5° достаточно ограничить ряд первыми четырьмя членами.
Получение более стабильных и точных результатов можно обеспечить использованием усреднения показаний датчика методом скользящего среднего. При реализации на основе дешёвого 8-битного микроконтроллера целесообразно выбрать число усредняемых измерений кратным степени двойки, тогда операция деления переходит в более простую операцию сдвига.
Существует много устройств, где не требуются очень точные измерения угла наклона, но необходим максимально простой и компактный алгоритм обработки. В этом случае возможно использование алгоритма вычисления значения угла наклона, основанного на элементарном двоичном делении, что удобно при применении дешёвых 8-битных микроконтроллеров (PIC, Atmel и т.д).
Рассмотрим первое выражение. При стабильных внешних условиях величина Т2 не изменяется. Тогда при S = 12,5% выражение можно преобразовать к виду:
A = Т1-Т2 (A = 0) / 12,5%·Т2
В диапазоне ±35° каждый градус наклона будет соответствовать ускорению примерно в 16 мg, где g - ускорение свободного падения. Используя это, при соответствующем выборе величины Т2 можно получить существенное сокращение вычислительных затрат за счёт применения двоичного деления. Например, пусть Т2 = 500 мкс, тогда при вертикальном положении датчика имеем изменение показаний ΔТ1 = (500 мкс) × 12,5% = 62,5 мкс, а изменение на 1 мкс соответствует 16 мg. Таким образом, изменение Т1 на 1 мкс соответствует наклону в 1°. Соответственно может быть использована любая кратная 500 мкс величина Т2 (например, 1000 мкс, 2000 мкс и т.д.).
Наиболее существенной ошибкой в этом случае является ошибка в определении величины коэффициента шкалы S. Для различных экземпляров датчиков значение S может изменяться от 10%/g до 15%/g, что приводит к ошибке ±8° при наклоне датчика ±40°. Другим источником ошибок является неточность задания Т2. Ошибка задания Т2 в 1% приводит к ошибке в 1% при вычислении угла.
Данные ошибки могут быть устранены точным подбором Т2 (для получения отношения 16 мg/мкс) с помощью выражения Т2 = 1 / 0,016 S. Например, при S = 10% получаем Т2 = 1 / (0,10 × 0,016) = 625 мкс. Увеличение Т2 до значения 625 мкс в этом случае устранит ошибки, вносимые коэффициентом шкалы S. Для точного подбора значения величины Т2 рекомендуется использовать схему, приведённую на рис. 4.
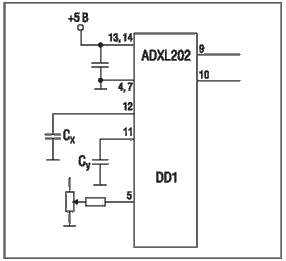
Рисунок 3 - Схема подбора значения периода T2
Для вычисления индивидуального для каждого датчика значения коэффициентов Toff и S необходимо проводить его предварительную калибровку. Архитектура ADXL202 такова, что калибровка может проводиться программно с помощью микроконтроллера. Вычисленные коэффициенты необходимо сохранить в энергонезависимой памяти контроллера и использовать в дальнейших вычислениях. Калибровка датчика проводится в два этапа:
1. Датчик располагается параллельно поверхности Земли. Считываются показания датчика, и вычисляется значение Toff.
2. Для калибровки значения S измеряют показания датчика при ускорениях ±1g, чувствительность определяется по двум измерениям. При калибровке ось акселерометра направляют вертикально к Земле. Измеряются показания X1 при 1g, далее датчик поворачивается на 180° и снимаются показания X2 при –1g. Тогда:
S = ( X1 – X2 ) / 2g
Например, пусть при измерениях получено X1 = 55%, X2 = 32%, тогда:
S = ( 55% – 32% ) / 2g = 11,5% / g.
Приведённая схема проста в изготовлении и настройке, позволяет проводить программную калибровку датчика, требует минимального количества внешних деталей и позволяет обеспечить точность измерения угла наклона 0,5° в двух плоскостях. Не требовательная к внешним условиям, устойчивая в работе и имеющая малые габариты, она может найти применение в системах ориентации, стабилизации, контроля и управления различных подвижных объектов.
1. Weinberg H. Dual Axis, Low g, Ffully Integrated Accelerometers. Analog Dialogue. 1999. Vol. 33. P. 23-26
2. http://www.analog.com/ru/index.html
3. Weinberg H. A Compact Algorithm Using the ADXL202 Duty Cycle Output