Снисарь Николай Александрович

Библиотека

Источник: Рабинер Л.Р., Шафер Р.В. "Цифровая обработка речевых сигналов." - Пер. с англ. / Под ред. Прохорова Ю.Н. Назарова М.В. - М: Радио и связь, 1981. - 496с.

 

    Цифровое представление речевых сигналов

5.0. Введение

     «Если бы я смог заставить поток электричества изменяться по интенсивности точно в соответствии с изменением плотности воздуха во время распространения звука, я мог бы записывать любые звуки, даже звуки речи» — А. Г. Белл [1]. Эта простая идея, имеющая столь важное значение для истории связи, кажется сегодня очевидной. Принцип, изложенный в от множества устройств и систем, предназначенных для записи, передачи или обработки речевых сигналов и в которых речевой сигнал отражает колебания плотности звуковых (речевых) волн.

      Рис. 5.1. Общая схема цифрового представления

      Это относится и к цифровым системам, в которых речевой сигнал представлен последовательностью своих мгновенных значений.
     Общая схема цифрового представления речевого сигнала изображена на рис. 5.1. Из рисунка следует, что речевое колебание как непрерывная функция времени подвергается дискретизации, чаще всего периодической, в результате которой образуется последовательность отсчетов х(пТ). Эти отсчеты могут в общем случае принимать непрерывное множество значений.
     Мы увидим далее, что рис. 5.1 достаточно полно отражает процесс формирования цифрового представления речевого сигнала.
     В начале главы изложены вопросы дискретизации применительно к речевым сигналам. Далее излагаются методы квантования отсчетов речевого колебания.

5.1. Дискретизация речевых сигналов

     Теорема дискретизации уже обсуждалась в гл. 2. В соответствии с изложенным в гл. 3 описанием гласных и фрикативных звуков речевой сигнал не ограничен по полосе частот, хотя его спектр быстро спадает в области высоких частот. На рис. 5.2 изображены спектры типичных звуков речи.

     Рис. 5.2. Спектры вокализованных звуков /а/ и /и/ и невокализованного /s/ при частоте дискретизации 20 кГц

     Видно, что для вокализованных звуков наивысшая частота, ниже которой максимумы спектра меньше уровня 40 дБ, составляет около 4 кГц. С другой стороны, для невокализованных звуков спектр не затухает даже на частотах выше 8 кГц. Таким образом, для точного воспроизведения всех звуков речи требуется частота дискретизации около 20 кГц. В большинстве приложений такая частота дискретизации, однако, не требуется. Например, если дис частот вокализованной речи, то достаточно располагать частью спектра до частоты около 3,5 кГц.

     Рис. 5.3. Типичная частотная характеристика тракта телефонной связи (по BTL, Transmission Systems for communication, стр. 73)

     Важная особенность, которую часто не замечают при обсуждении дискретизации, состоит в том, что даже если сигнал имеет ограниченный по частоте спектр, он может быть искажен широкополосным случайным шумом перед аналого-цифровым преобразова нием. В таких случаях смесь сигнала и шума должна быть про пущена через фильтр с частотой среза, близкой к частоте Найквиста, что позволит избежать эффекта наложения частот при цифровом представлении.

5.2. Обзор статистических моделей речевых сигналов

     При рассмотрении цифровых методов представления часто до является большим упрощением, далее будет показано, что статистическая точка зрения приводит к полезным результатам, тем самым подтверждая целесообразность подобной модели.
     Если предположить, что сигнал xa(t) представляет собой непрерывный случайный процесс, то периодическая последователь рассматриваться как случай являются одномерная функция плотности вероятности и автокорреляционная функция, определенная выражением

     (5,1)

      где E[] означает усреднение по ансамблю величины, стоящей в квадратных скобках. Непрерывная спектральная плотность мощности представляет собой преобразование Фурье от

     (5.2)

     Сигнал с дискретным временем, полученный из непрерывного сиг нала, имеет автокорреляционную функцию

     (5.3)

     Это просто дискретизированная функция поэтому спектральная плотность мощности равна

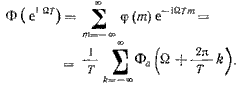     (5.4)

     Из (5.4) следует, что спектральная плотность дискретизированного сигнала представляет собой периодическую последовательность, каждый член которой повторяет спектр аналогового сигнала.
     Функция плотности вероятности величины х(п) такая же, как и величины xa(t), так как х(п) =хa(пТ). Это означает, в свою оче непрерывного сигнала и сигнала с дискретным временем одинаковы.
     Для использования статистических понятий при описании речевых сигналов необходимо оценить функцию плотности вероятно (или спектральную плотность мощности) речевого колебания. Функция плотности вероятности оценивается путем определения гистограммы по большому числу отсчетов, т. е. в течение большого отрезка времени. Давенпорт [2] провел обширные исследования такого рода, а позже Паез и Глис-сон [3], используя сходные измерения, показали, что хорошей аппроксимацией для экспериментальной функции плотности вероятности может служить гамма-распределение

     (5.5)

     Более простой аппроксимацией является функция плотности вероятности Лапласа

     (5.6)

     На рис. 5.4 показана экспериментальная функция плотности вероятности совместно с функцией плотности вероятности Лапласа и гамма-распределением. Все функции нормализованы таким обра зом, что среднее значение равно нулю, а дисперсия — единице. Хо вероятностей хорошо аппроксимируют экспериментальный результат, гамма-распределение, очевидно, обеспечивает лучшую аппроксимацию.

     Рис. 5.4. Функции плотности вероятности гамма-распределения и распределения Лапласа [3]

     Автокорреляционная функция и спектральная плотность мощ временных рядов. Оценка автокорреляционной функции зргодического случайного процесса может быть получена путем усреднения за большой отрезок времени. На пример, для получения усреднения за большой интервал времени достаточно немного изменить определение кратковременной автокорреляционной функции (4.30):

     (5.7)

     где L — большое целое число. Пример такой оценки показан на рис. 5.5 при частоте дискретизации 8 кГц [4]. Верхняя кривая вычислена по сигналу, пропущенному через фильтр нижних час тот, нижняя — через полосовой фильтр. Заштрихованные области вокруг каждой кривой показывают изменения в корреляции, воз быстро убывает при увеличении расстояния между ними. Видно, что речевой сигнал на выходе фильтра нижних частот более коррелирован, чем на выходе поло сового фильтра.

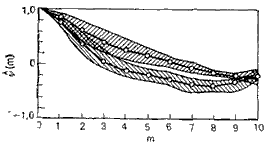
     Рис. 5.5. Автокорреляционная функция речевых сигналов: верхняя кри вая— для низкочастот ной составляющей речи, нижняя — для высоко частотной [4]

     Спектральную плотность мощности можно оценить различными путями. На рис. 5.6 показан пример, в котором мощность усреднялась за минуту непрерывной речи.

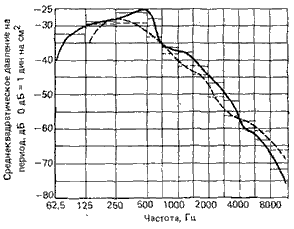
     Рис. 5.6. Усредненная спектральная плотность мощности непрерывного речевого сигнала [5]:
шесть дикторов-мужчин:: пять дикторов-женщин соответственно

     Этот рисунок показывает, что усредненная спектральная плотность мощности имеет максимум в диапазоне 250—500 Гц и затухает примерно на 8—10 дБ на октаву. Другой подход к оценке усредненной спектральной плотности состоит в оценивании и последующем вычислении

          (5.8)

     при k=0, 1,.., N—1, используя дискретное преобразование Фурье [6], где w(m) окно (взвешивающая функция) для автокорреляционной функции. В качестве примера применения этого метода к оценке спектральной плотности речи на рис. 5.7 приведены соответствую один подход состоит в вычислении передаточной функции цифрового фильтра, на входе которого действует белый шум, а сигнал на вы свойства, что и данный сигнал (см. гл. 8).

     Рис. 5.7. Автокорреляционная функция (а) и спектральная плотность мощности (б) речевого сигнала [7]

5.3. Квантование мгновенных значений

     Так же, как полезно разделять операции дискретизации и квантования, целесообразно разделить процесс представления последовательности {x(n)} множеством символов на два этапа: квантование, результатом которого является последовательность величин {х(п)} = {Q[x(n)]}, и кодирование, при котором каждой квантованной величине ставится в соответствие кодовое слово с{п). Этот процесс изображен на рис. 5.8а. Аналогично определим декодер как устройство, которое последовательности кодовых слов {с'(п)} ставит в соответствие последовательность квантованных отсчетов {х'(п)}, как это показано на рис. 5.86.

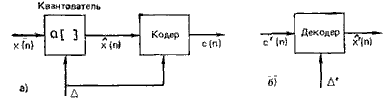
     Рис. 5.8. Квантование и кодирование: а) кодер; б) декодер

     Если последовательность точно совпадает с последовательностью кодовых слов с(п), т. е. ошибки отсутствуют, то сигнал на выходе идеального декодера точно совпадает с последователь­ностью квантованных отсчетов входного сигнала, т. е. х'(n)=х(n).

     где F — частота дискретизации (т. е. отсч./с); В — число бит на отсчет сигнала. В общем случае желательно выбирать скорость передачи наиболее низкой, при которой еще сохраняется требуемое качество восприятия сигнала.
     В общем случае целесообразно предполагать, что отсчеты сигнала будут попадать в конечный интервал значений, при котором

     Для удобства следует предположить, что величина Хmax бесконечно велика, что соответствует, например, функциям плотности вероятности Лапласа. Однако следует иметь в виду, что предположение о конечности диапазона значе описания сигнала используется функция плотности вероятности Лапласа, то легко показать (см. задачу 5.2), что только 0,35% от диапазона:

     Таким образом, целесообразно считать, что полный размах сигнала пропорционален среднему квадратическому отклонению.
     Диапазон изменения входного сигнала делится на интервалы, и операция квантования сводится к тому, что всем отсчетам вход некоторый интервал, приписывается одно и то же заданное значение.

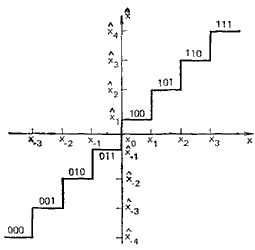
     Этот процесс иллюстрирует рис. 5.9 для восьми-уровневого квантователя. В принципе можно использовать все восемь способов обозначения уровней, однако часто имеются причины выбирать вполне определенный способ кодирования.

...

© ДонНТУ, Снисарь Николай Александрович, 2008