Снисарь Николай Александрович

Библиотека

Источник: Аграновский А.В., Леднов Д.А. "Теоретические аспекты алгоритмов обработки и классификации речевых сигналов". -Москва: Радио и связь, 2004. -164 с.

 

Глава 1. ОБНАРУЖЕНИЕ, ФИЛЬТРАЦИЯ И ПАРАМЕТРИЗАЦИЯ РЕЧЕВОГО СИГНАЛА

1.1. Обнаружение речевого сигнала

     Детектор речи предназначен для выделения из входного зву кового потока, состоящего из смеси полезного сигнала и шума, непрерывной последовательности сегментов, содержащих закон стохастических сигналов, которая описана во многих публикациях (например, [11, 18]). Здесь кратко изложим основные положения этой теории. Пусть - значение аддитивного шума в дискретный момент времени t, полученное в результате оцифровки АЦП аналогового шума через равные интервалы времени At, e(t) -значение полезного сигнала (речи) в дискретный момент времени t, тогда у[t] — значение наблюдаемого сигнала может быть записано в виде где Th — случайная величина, определенная на множестве {0,1};
     По значению наблюдаемого сигнала нам необходимо при сигнала нет: d0=0, и полезный сигнал есть: d=1. Пространство реализаций наблюдаемого сигнала должно быть разбито на два подпространства, каж которых соответствует определенному решению. Пусть подпространство d0 соответствует решению d0, а пространство O, решению d1. Однако принимаемые решения могут быть ошибочными, и для того чтобы характеризовать эти ошибки вводится показатель риска:

     (1-2)

     (1-3)

1.1.1 Обнаружение в условиях стационарного шума

     Рассмотрим соотношение между оценками случайного про цесса во временной и частотной областях. Известно, что несмещенной оценкой математического ожидания случайного процесса yt является величина:

     (1-4)

     Найдем дискретное преобразование Фурье (ДПФ) на интервале Т (допустим, что это возможно):

     (1-5)

     Очевидно, что дробь в последнем выражении (1.5) равна нулю за исключением случая к=0, откуда заключаем, что оценка математического ожидания всегда равна нулевому коэффициенту ДПФ случайного процесса.
     Далее докажем утверждение, что если процесс стационарен, то оценка математического ожидания любой компоненты спектpa — постоянная величина. Для этого проведем вычисления, соответствующие ОДПФ компонент случайного процесса:

     Вычисления показывают, что независимость корреляционной функции от времени обеспечивает справедливость утверждения.
     Выражение (1.6) позволяет проводить исследование стационарного случайного процесса не во временной области, а в частотной, что практически более удобно, так как появляется возможность игнорировать фазы гармоник, которые не влияют на восприятие звуков речи человеком.
     Рассмотрим поведение нестационарного полезного сигнала в евклидовом пространстве спектральных компонент. Динамика этих компонент отображается траекторией, которая может быть целиком помещена в некоторую замкнутую область Q. Траектория стационарного шума так же может быть помещена в замкнутую область д. Если области Q и q пересекаются слабо или вообще не пересекаются, то речь можно описать некоторым распределением вероятности, присущим стационарному процессу.
     Предположим, что плотность распределения вероятности спектральных компонент как шума, так и полезного сигнала имеют гауссову форму

     (1-7)

     где h[i]. — значение /-ой спектральной компоненты; m — вектор математических ожиданий спектральных компонент;

     (1-8)

     D — корреляционная матрица, элементы которой определены как

     (1-9)

     Классифицировать тот или иной входной сигнал, в смысле (1.1), который в момент времени t обладает вектором спектральных компонент h[t] возможно с помощью байесовского ре (1.4), аргументы которого могут быть записаны в виде

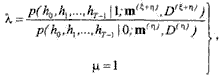     (1-10)

     где (m(n), D(n)), (m(n+e), D(n+e)) — параметры распределения плотности вероятности, соответственно шума и смеси шума с полезным сигналом, вероятность наличия полезного сигнала p[1]=1/2 и значения функции потерь равны K(0,1)=K(1,0)= 1.
     После того, как выбрана вероятностная модель сигнала (1.7) и стратегия принятия решения (1.10), необходимо оценить параметры распределений (1.8) и (1.9). Практически это означает, что требуется создать две достаточно представительные выборки случайных процесс. Конечно, такую работу мож но провести «в ручную», т.е. опытный оператор проведет сортировку записей речевых сообщений и выделит два необходимых класса выбо предпочтителен вариант автоматического создания та ких выборок. Для автоматизации процесса мы должны построить более простой, но достаточно точный метод классификации сигнала.
     Поскольку в качестве модели случайного процесса выбрана его аддитивная форма (1.1), то это позволяет предполагать, что среднее значение квадрата амплитуды смеси полезного сигнала и шума будет превышать среднее значение квадрата амплитуды шума.
     Сигнал, содержащий только шум, как правило, получить не представляет сложности. Например, в системах, где обеспечен ввод речи с помощью микрофона, внутренний шум системы и внешний могут быть записаны в режиме молчания диктора, а в системах, где ввод обеспечен телефонным каналом, есть достаточное время от момента снятия трубки до начала беседы (око 0,5 с).
     Предположим, что среднее значение квадрата амплитуды шума на интервале Т распределено по нормальному закону:

     (1-11)

     (1-12)

     (1-13)

     (1-14)

     G — количество интервалов длительностью Т, выбранных для оценки параметров распределения (1.12).
     где Н — порог,
     Классифицируем сегменты, содержащие полезный речевой сигнал с помощью условия которое при логарифмировании приводит к следующему неравенству

     (1-15)

     Таким образом, для построения детектора речи на фоне стационарного шума необходимо выполнить следующие операции:

1. Создать запись, содержащую только шум.
2. На основе этой записи рассчитать параметры распределения (1.12), т.е. вычислить дисперсию и математическое ожидание по формулам (1.13) и (1.14).
3. На основе этой же записи оценить параметры распределения (1.7) для шума, т.е. вычислить (1.8) и (1.9). На рисунке 1.1 показано математическое ожидание (сплошная линия) и сумма математического ожидания и двукратной дисперсии (пунктирная линия) распределения (1.7) с диагональной корреляционной матрицей для шума компьютерного вентилятора.

4. Создать запись, содержащую речь.
5. Классифицировать сегменты этой записи с помощью условия (1.15)
6. На основе сегментов классифицированных как смесь полезного сигнала и шума оценить параметры распределения (1.7).
   На рисунке 1.2. показано математическое ожидание (сплошная линия) и сумма математического ожидания и двукратной дисперсии (пунктирная линия) распределения (1.7) с диагональ ной корреляционной матрицей для речи.

Рис. 1.2. Распределение вероятностей спектральных компонент речи

7. Классифицировать новый входной сигнал с помощью решения Байеса с аргументами (1.10).
   

     Очевидно, что этот класс моделей является перспективным, а его развитие может быть направлено по двум путям:
     а) поиск распределений вероятностей, которые могут более точно аппроксимировать данные об амплитудах компонент, как спектра шума, так и спектра речи. Для примера, распределение Гаусса в формуле (1.7) может быть замещено или смесью гауссоид, параметры которой можно найти с помощью известного ЕМ-алгоритма [21], описанного в приложении 2, или нормальным процессом авторегрессии [17] с алгоритмом обучения, приведенным в работе [22] (см. раздел п.1.1.2);
     б) выделение значимых компонент спектра шума и их функций, наиболее достоверно позволяющих отличить шум от полезного сигнала. Эту операцию можно выполнить с помощью МГУА [23], который также будет описан ниже.

1.1.2. Обнаружение речи в условиях марковского шума

     В отличие от постановки задачи, описанной в предыдущем параграфе, где нам были известны распределения шума и смеси полезного сигнала и шума, здесь рассмотрим случай, когда известны отдельно статистические свойства речи и статистические свойства шума, а наблюдается их смесь. В качестве статистических моделей шума и речи используем СММ [17].
      В дополнении к обозначениям и определениям, принятым для СММ в приложении 1, введем обозначения, которые нам потребуются в рамках этого параграфа:
     h[t] вектор наблюдения, составленный из компонент спектра Фурье входного сигнала, h[t] причем h[t]=Th*x[t] +z[t] здесь х[t],z[t] — вектора компонент спектра Фурье полезного сигнала и шума, соответственно;
     Z = {z[0], z[1] ..., z[G-1]} — предполагаемая последовательность значений шума;
     U = {и[0], u[1] ..., u[G-1]} — некоторая произвольная последовательность состояний полезного сигнала;
     V={v[0],v[1],...,v[G-1]}- некоторая произвольная последовательность состояний шума;
     В дальнейшем для упрощения записи вероятностей будем ис пользовать только индексы текущих состояний последовательности.
     Рассмотрим два способа обнаружения полезного сигнала. Пер наиболее вероятной траектории на обобщенном множестве состояний смеси полезного сигнала и шума и чистого шума.

     Первый способ. Будем предполагать, что априорная вероятность равна соответственно m=1, а для отношения правдоподобия справедливо

     (1-16)

     где p(U,V|1) — вероятность последовательности смеси состояний шума и полезного сигнала. Очевидно, что в силу их независимости справедливо

     (1-17)

     где p(U,V | H; 1) — условная вероятность последовательности смеси состояний шума и полезного сигнала при реализации последовательности наблюдений H. Опять же в силу независимости состояний сигнала и шума и при условии, что известны значения шума в каждый момент времени, для нее справедливо

     (1-18)

     где p(V*|0) -- вероятность последовательности состояний шума V (звездочкой отмечено то, что состояния чистого шума не со p(V*|H ; 0) — вероятность последовательности состояний шума F* при наблюдении последовательности H.
     Раскроем выражение (1.16), используя (1.17) и (1.18):

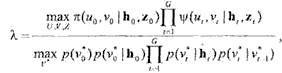     (1-19)

     где для сокращения записи введены обозначения

     Рассмотрим вариант упрощения вычислений в (1.19) за счет суммирования состояний шума и полезного сигнала.
     Пусть Ss — {s} — множество состояний полезного сигнала, содержащее их ровно Ns штук, a Sd = {6} — множество состоя тогда множество сме множества S и условных вероятностей справедливы соответствующие соотношения

     (здесь мы вводим перенумерацию смешанных состояний, чтобы в дальнейшем пользоваться для их обозначения одним индексом).
     Последовательность (1.19) можно записать в виде:

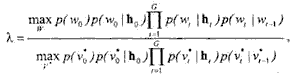     (1-21)

     Несмотря на значительное упрощение отношения правдоподобия (1.19), за счет построения множества смешанных состоя само вычисление значе ия (1.21) по прежнему остается трудоемким из-за двукратного использования метода динамического программирования (при условиях жестких требований ко времени обнаружения такой метод неприменим. Более простым является способ, использующий механизм разладки, впервые предложенный в работе [24]. Суть этого метода состоит в том, чтобы в каждый момент времени вычислять логарифм коэффициента правдоподобия в виде

     (1-22)

     Затем рассчитывать кумулятивную сумму логарифмов коэффициентов правдоподобия по правилу

     (1-23)

     и следить за ее знаком. Если знак (1.23) положительный, то наблюдается полезный сигнал, в противном случае — шум.
     Как показано в [17], такой подход справедлив только в случае, если диагональные элементы матриц вероятностей переходов между состояниями много больше недиагональных. Второй способ. Пусть имеется множество состояний случай ного процесса S, которое состоит из состояний, соответствующих смеси речи и шума и состоянии чистого шума Тогда вероятность, что данная последовательность состояний О определена данной последовательностью наблюдений будет равна

     (1-24)

     Используя метод динамического программирования (для обнаружения сигнала, необходимо выделить из последовательности состояний О* та кие цепочки состояний, номера которых меньше, чем NsNd— 1.
     Необходимо отметить, что матрица переходов определена отдельно для состояний с номерами меньшими NsNd — 1 и от числа, т.е. вероятности переходов из состояний шума в смешенные состояния и обратно равны нулю. В этой ситуации можно только предположить, что такие переходы равновероятны. Это предположение приводит к тому, что матрица переходов пересчитывается в соответ ствии с нормальными стохастическими условиями (приложение 1):

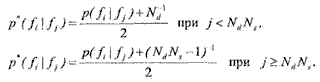     (1-25)

     Итак, к настоящему моменту нами были рассмотрены три метода классификации случайного процесса на два класса (шум и речь): два из них основаны на байесовском решении и один
на максимизации апостериорной вероятности. Однако для того чтобы их использовать, необходимо проделать еще не-только операций:
     1) найти множество состояний случайного процесса;
     2) выбрать вид функций условных плотностей распределения вероятностей р(fj |ht);
     3) найти параметры этих функций;
     4) вычислить матрицы переходных вероятностей между состояниями.

     Найдем множество состояний для случайных процессов, со количеством выборок, для того чтобы определить статистические свойства шума. Что касается речи, то можно поступить следующим способом: провести исследование статистических свойств речи в условиях слабого стационарного шума, который может быть выделен детекто в случае шума, — собрать достаточное количество выборок полезного сигнала.
     С помощью ДПФ преобразуем полученные выборки в последовательности векторов акустических параметров Н = {h0,h1,...,h[N-1]..,}
и проведем кластеризацию векторов акустических параметров сигнала с помощью известного метода минимакс, описанного в [25]. Здесь изложим суть этого метода.
     Пусть необходимо сортировать данные Н = {h[0],h[1] ,...,h[N-1],} на
М кластеров k[i] i=1,...,М (причем М неизвестно), и задана мера удаленности двух векторов d(h[i], h[j]). В качестве меры удаленности можно выбрать евклидово расстояние, расстояние Махаланоби-са [26] или др.
     Проиллюстрируем этот метод, используя шесть векторов в выборке (N=5). На первом этапе разместим N+1 векторов в таблице, произвольно припишем вектору у0 кластер к0 (рис. 1.3, а). Затем найдем вектор наиболее удаленный от кластера к0, например h4; припишем вектору h4 кластер к} (рис. 1.3, о). Теперь найдем кластер, ближайший к каждому из векторов и запомним эти минимальные расстояния. Найдем наибольшее из этих минимальных расстояний и отнесем соответствую вектор к категории кг Предположим, что этим вектором является вектор h5 (рис. 1.3, в). Теперь для остальных векто ближайший к каж дому из векторов и запомним расстояния. Найдем наибольшее из этих наименьших расстояний

     Рис. 1.3. Постороение кластеров методом минимакс

     В качестве функции условной плотности вероятности акустических параметров состояний p(fj|hi) можно выбрать функ наблюдаемых векторов, отнесенных к тому или иному кластеру по формулам (1.8) и (1.9), найдем корреляционную матрицу и математическое ожидание этих распределений.
     Найдем элементы матрицы переходных вероятностей p(fi|fj). В работе [17] показано, что на основе метода обратной связи можно рассчитать эту матрицу как отношение частоты встречи состояния / после состояния /, к общей частоте встречи состоя ния /. Считается, что в момент времени t встречено состояние i, если выполняется условие i = argmax p( f} | h) .
     Таким образом, для построения детектора речи на фоне не стационарного шума, имеющего Марковский характер, необходимо выполнить следующие операции:

1. Создать записи сигналов, содержащих только шум.
2. Создать записи, которые содержат речь в стационарном шуме с известными статистическими свойствами.
3. На базе этих записей методом минимакс определить множества состояний шума и полезного сигнала.
4. Для каждого состояния определить плотность распределения вероятностей вида (1.7) с корреляционной матрицей (1.8) и математическим ожиданием (1.9).
5. Найти значения матрицы переходов между состояниями.
6. Найти отношение между минимальным диагональным элементом матрицы вероятностей переходов и ее максимальным недиагональным элементом. Если это отношение много больше единицы, то наличие речи в поступающем на вход детектора сигнале можно определять на основе механизма разладки (1.22)— (1-23).
7. Если отношение между минимальным диагональным элементом матрицы вероятностей переходов и ее максимальным недиагональным элементом имеют один и тот же порядок, то необходимо использовать метод динамического программирования (приложение 1.2), т.е. найти оптимальную траекторию неизвестного входного сигнала на каждом интервале анализа и по формуле (1.21) определять значение коэффициента правдоподобия, который является показателем наличия речи в поступающем на вход детектора сигнале.

     Как и в случае детектирования речи в стационарном шуме, представленные модели могут быть развиты в направлении поиска распределений вероятностей, которые могут более точно описывать распределения амплитуд компонент, как спектра шума, так и спектра речи в состояниях СММ.

1.2. Фильтрация речевого сигнала и его восстановление

     В общем случае фильтрация сигнала состоит в том, чтобы выделить полезную составляющую сигнала :

• необходимо выделить полезный сигнал из высокочастотного или полосового шума. В этом случае фильтрация заключается в выборе типа фильтра и расчете его параметров [11];
• требуется выделить речевой сигнал из речеподобного шума [4]. Например, два или более дикторов могут говорить одновременно, а требуется получить разборчивую речь только одног из них. Это одна из самых сложных задач фильтрации, общих методов решения которой пока нет;
• требуется восстановить сигнал, потерпевший нелинейные искажения. Эта задача возникла с появлением цифровых телефонных линий, которые уплотняют речь при передаче и искажают исходный сигнал.

...

© ДонНТУ, Снисарь Николай Александрович, 2008