Источник: Fundamental principles of the electromagnetic flow measurment, Krohne Messtechnik GmbH and Co, Duisburg 2003

     Electromagnetic flowmeters (EMFs) Friedrich Hofmann, Dipl.-Ing., D-47058 Duisburg Principle and theory, in brief: Principle The figure shows the basic setup of an electromagnetic flowmeter (EMF) for completely filled pipelines. The EMF consists of a non-ferromagnetic measuring tube with an electrically insulating inner surface, and magnetic coils and electrodes that are arranged diametrically on the tube and are in contact with the process liquid through the tube wall. The field coils through which current flows generate a magnetic field with induction B perpendicular to the longitudinal axis of the tube.

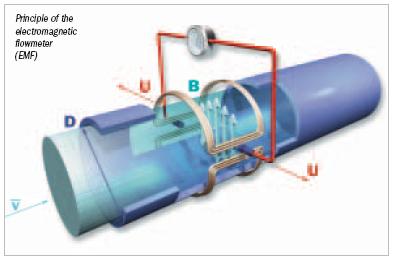
     This magnetic field penetrates the measuring tube and the process liquid flowing through it, which must be electrically conductive. In accordance with the law of induction, a voltage Ui is induced in the process liquid that is proportional to the flow velocity v – of the process liquid, induction B and the inside tube diameter D. In simplified form, the following expression is applicable: Ui = k • B • D •v – This signal voltage Ui is picked up by electrodes that are in conductive contact with the process liquid and insulated from the tube wall. Using q =v • D2 / 4 the signal voltage Ui is converted by a signal converter into a flow indication qi qi = Ui • D 4 • k • B and converted into standardized signals appropriate to the process. Theory of electromagnetic flow measurement Faraday [1] propounded his law of induction in 1832. This law describes the voltage Ui induced in an electrically conductive body while passing through a magnetic field: Ui = (v x B) • L > where: Ui = induced voltage (vector) >B = induction (vector) L = length of conductor moving through a magnetic field, and v = its velocity (vector) Faraday attempted to determine the flow velocity of the River Thames in 1832 by measuring the voltage induced in flowing water by the earth’s magnetic field.

     Thurlemann [2], Shercliff [3] investigated the properties of electromagnetic flowmeters. For a theoretical model with an infinitely long homogeneous magnetic field and point electrodes, it was established that the measuring voltage is independent of the flow profile in the measuring tube provided the flow profile is radially symmetrical. On these assumptions, we obtain the flow-proportional signal voltage Ui as: Ui = k • B • D • vv – where: Ui - induced flow-proportional signal voltage k - non-dimensional constant B - induction D - electrode spacing (measuring tube to inside diameter) v – mean velocity of the process liquid Shercliff recognized that the contribution of the finite elements of flow in the measuring tube towards the total signal voltage is weighted as a factor of their location in the measuring tube, and created the term valence vector. Proceeding from Maxwell’s equations, he showed that the following applies to the electrode signal voltage U:

...