Источник: Дж. Бэтчелор, "Введение в динамику жидкости". Москва, Мир 1973
      1.6. Явления переноса

     Равновесные состояния вещества характеризуются равномер­ным распределением в пространстве всех его параметров, причем каждый элемент вещества находится в механическом и тепловом равновесии с соседними элементами. Если некоторые параметры вещества в исходном состоянии распределены неравномерно, то между соседними элементами вещества происходит механиче­ский или тепловой обмен, который всегда приводит вещество в равновесное состояние, т. е. стремится сгладить имеющиеся в нем неоднородности. Существование этого стремления к равно­весию в неоднородном веществе, которое в классической термоди­намике принимается без доказательства, по-видимому, требует только, чтобы смежные части вещества взаимодействовали опре­деленным образом. Характер этого взаимодействия может зави­сеть от молекулярного строения смежных частей вещества и от физических свойств процессов переноса, зависящих от конкрет­ного параметра, который распределен неравномерно, однако тен­денция к равновесию между взаимодействующими частями вещест­ва имеет вполне общий характер и не зависит, как и все резуль­таты классической термодинамики, от конкретного строения дан­ного вещества.

     Важный и общий результат обмена между двумя элементами вещества с различными параметрами состоит в том, что величина некоторого количества, удовлетворяющего закону сохранения, связанная с одним элементом, уменьшается, а величина, связан­ная с другим элементом, увеличивается. В целом ряд таких обменов составляет то, что называют явлением переноса. Три основных вида этого явления — это переносы вещества (массы), энергии и количества движения. Основное внимание в этом пара­графе обращено на общие свойства этих трех видов переноса. Мы не будем привлекать конкретные молекулярные свойства вещества, хотя иногда на них придется ссылаться для удобства и выяснения природы молекулярного механизма переноса в жид­костях.

     В жидкой смеси, состав которой изменяется в зависимости от координат, возникает перенос вещества особого вида. Пред­положим, что молекулы одной составной части смеси отмечены определенным образом. Все молекулы находятся в непрерывном хаотичном движении и вследствие этого имеют тенденцию к уда­лению от какого-либо начального положения. В таком случае если в некоторый момент времени количество отмеченных молекул вблизи одной стороны элемента поверхности, проведенной в жид­кости, больше чем на другой, то случайное блуждание отмеченных молекул в обоих направлениях через элемент поверхности приво­дит в общем случае к ненулевому потоку молекул через него; направление этого потока таково, что он приводит к выравнива­нию количества отмеченных молекул с обеих сторон от поверх­ности 2). Этот ненулевой поток одной из частей жидкой смеси, создаваемый перемещением самих молекул, порождает диффузию вещества (массодиффузию). Обсуждение этого весьма сложного явления будет ограничено случаями малой концентрации диф­фундирующей части смеси.

      Перенос кинетической энергии молекулярного движения осу­ществляется путем взаимодействия соседних молекул (или в ре­зультате столь малых расстояний между молекулами, что одна находится в пределах действия поля сил другой, как в случае твердых тел и жидкостей, или в результате случайных столкнове­ний, как в случае газа). Условия, при которых происходит пере­нос только энергии молекул, т. е. тепловой энергии, известны из эксперимента. Две массы жидкости, разделенные тонкой жест­кой стенкой, проницаемой для тепла, находятся в тепловом равно­весии, если функция состояния, называемая температурой, имеет одинаковые значения для этих масс; а если две температуры не равны, то существует некоторый ненулевой поток тепла через границу в направлении убывания температуры. Удаление стенки, разделяющей эти две массы при одном и том же давлении, очевид­но, не влияет на условие теплового равновесия или на направле­ние указанного теплового потока в том случае, когда две темпера­туры различны, хотя величина теплового потока изменяется ввиду того, что давления при отсутствии стенки должны оставаться одинаковыми. Этот поток энергии молекул, когда температура распределена неравномерно, создает теплопроводность.

      Перенос количества движения молекул через элемент поверх­ности, движущейся с локальной макроскопической скоростью жидкости, возникает в том случае, когда молекулы пересекают поверхность, и он всегда происходит, если имеется сила взаимо­действия между двумя группами молекул на обеих сторонах эле­мента поверхности. Суммарный эффект потока количества движе­ния при прохождении молекул через элемент поверхности и сил, создаваемых между молекулами на его обеих сторонах, представ­ляется в виде локального напряжения в жидкости. Напряжение в какой-либо точке жидкости есть результат движения молекул и их взаимодействий в окрестности этой точки, поэтому если скорость жидкости постоянна в этой окрестности, то напряжение имеет вид, соответствующий покоящейся жидкости, и направ­лено по нормали к элементу поверхности при любой его ориента­ции. Если же скорость жидкости непостоянна в этой окрестности, то касательные напряжения могут быть отличными от нуля.

      Закон изменения векторной функции координат, например скорости жидкости, в окрестности какой-либо точки не очевиден и будет рассмотрен в гл. 2; напряжение, связанное с этим изме­нением скорости, будет полностью описано в гл. 3. Однако пока можно использовать понятие переноса количества движения в рам­ках предварительного обсуждения, ограничиваясь частным слу­чаем (имеющим, однако, как будет установлено позже, фунда­ментальное значение), когда скорость жидкости по отношению к элементу поверхности (движущемуся вместе с жидкостью) рас­положена в его плоскости и имеет величину, которая изменяется только по нормали к этому элементу поверхности; такое движение называется простым сдвигом, при котором плоскости жидкости, параллельные элементу поверхности, скользят как жесткие друг над другом. В этих условиях очевидно, что если скорости жид­кости по обе стороны элемента поверхности различны, то любое случайное взаимодействие молекул через этот элемент приводит к появлению касательной составляющей напряжения, а знак напряжения будет таким, который соответствует уменьшению разности скоростей по обе стороны от элемента поверхности. Перенос количества движения создает таким образом внутреннее трение, а жидкость, в которой проявляется внутреннее трение, называется вязкой.

      Основные общие свойства всех трех видов переноса состоят в следующем: во-первых, результирующий поток некоторой вели­чины (числа отмеченных молекул, тепла, количества движения) равен нулю тогда, когда связанная с ней другая величина, харак­теризующая локальную интенсивность (долю отмеченных моле­кул, температуру, скорость жидкости), распределена равномерно в пространстве; во-вторых, направление движения ненулевого результирующего потока через элемент поверхности в веществе таково, что происходит выравнивание интенсивности по обе его стороны.

     Приступим теперь к рассмотрению количественного соотно­шения между результирующим потоком и неоднородностью свя­занной с ним локальной интенсивности. Предварительно отметим, что, хотя наличие или отсутствие равновесия в классической термодинамике показывается на основании следствий контакта двух масс, каждая из которых однородна, в механике сплошной среды обычно приходится рассматривать такие состояния, в кото­рых интенсивность представляет собой функцию координат. Очевидно, что явление молекулярного переноса при неравномер­ном распределении величины интенсивности в окрестности эле­мента поверхности приводит к результирующему потоку через элемент поверхности в веществе; однако вместо представления этой локальной неравномерности разностью значений интенсивностей по обе стороны элемента нужно придерживаться более общей точки зрения и представить ее в виде вектора градиента интенсив­ности в каждой точке поверхности.

     Линейное соотношение между потоком и градиентом скалярной интенсивности

      Рассмотрим сначала случаи, в которых соответствующая интенсивность представляет собой скалярную величину (а имен­но количество отмеченных молекул или температуру), которую обозначим С (как это принято для концентрации). Предполагает­ся, что С — непрерывная функция координаты х в веществе и, возможно, также времени t, хотя время не будет оказывать явного влияния на процесс переноса в фиксированный момент времени. Теперь результирующий поток величины, связанной со скалярной величиной С, через элемент поверхности в веществе на единицу ее площади представляет собой локальную величину, которая изменяется с изменением направления нормали n к по­верхности элемента, точно так же, как компонента некоторого вектора в направлении нормали n. Это формально следует из рас­суждения, подобного тому, которое приводит к выражению (1.3.4) для напряжения: сумма направленных внутрь потоков через три ортогональные грани малого тетраэдра отличается от потока, выходящего из тетраэдра во внешнюю часть пространства через его наклонную грань, только на величину порядка объема тетра­эдра. Следовательно, результирующий поток (перенос в секунду) через элемент поверхности с площадью А и нормалью n равен произведению

      Первая часть нашего предположения заключается в том, что для достаточно плавного и постепенного изменения величины интенсивности С относительно некоторой точки в веществе поток f зависит только от локальных свойств среды и локальных значе­ний С и deltaС. Идея здесь проста: перенос через элемент поверхности определяется движениями молекул и их взаимодействиями в окре­стности элемента поверхности и во всей этой области величина С может быть аппроксимирована линейной функцией координат, если удовлетворяется некоторое условие: отношение

      где поток f зависит от х (и, возможно, также от времени t), но не зависит от нормали n.

      Наша задача состоит в том, чтобы установить соотношение между двумя функциями координат, С и f. О прямом вычислении потока, исходя из рассмотрения молекулярного процесса, почти не может быть и речи для жидкостей и твердых тел, и лишь в слу­чае газов (рассматриваемом в следующем параграфе) такое вычис­ление оказывается отчасти успешным. Требуется ввести некоторое предположение, и лучше всего независимое от действительного характера основного молекулярного механизма, чтобы оно было применимо для возможно широкого круга веществ. Это предполо­жение, к изложению которого мы сейчас приступаем, первона­чально основывалось на измерениях переноса в конкретных физических задачах и использовалось только в таких задачах, однако затем было обнаружено, что оно имеет более общее зна­чение.

      Первая часть нашего предположения заключается в том, что для достаточно плавного и постепенного изменения величины интенсивности С относительно некоторой точки в веществе поток f зависит только от локальных свойств среды и локальных значе­ний С и deltaС. Идея здесь проста: перенос через элемент поверхности определяется движениями молекул и их взаимодействиями в окре­стности элемента поверхности и во всей этой области величина С может быть аппроксимирована линейной функцией координат, если удовлетворяется некоторое условие: отношение

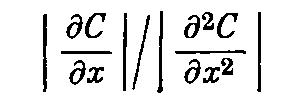
      значительно больше характерной длины молекулярного движения или взаимодействия, как обычно и бывает на практике. Вторая часть предположения состоит в том, что для достаточно малых значений |deltaС| поток f изменяется линейно с изменением компо­нент вектора |deltaС|. Известно, что поток обращается в нуль в случае обращения в нуль |deltaС| , так что наше предположение можно выразить в виде

      Как поток lг, так и производная дС/дх^2 — векторы, а требование о том, чтобы соотношение (1.6.1) было справедливо при любом выборе системы координат, показывает, что коэффициент переноса кц представляет собой тензор второго порядка. Коэффи­циент км зависит от локальных свойств вещества (т. е. от локаль­ного термодинамического состояния вещества) и, возможно, также от локального значения С, но не от градиента deltaС. С математиче­ской точки зрения соотношение (1.6.1) можно рассматривать как предположение о том, что в разложении вектора f в ряд Тейлора по компонентам вектора deltaС члены второго и более высокого порядка малости пренебрежимо малы.

      Это общее предположение можно дополнить другими пред­положениями, опирающимися на известные свойства конкретных материалов. Для однородных материалов коэффициенты кц могут зависеть от координат точки только посредством зависимости от локального значения С; обращение направления вектора deltaС должно приводить к обращению направления потока F, поэтому в рассматриваемом случае члены второй и других четных степе­ней ряда Тейлора для вектора l тождественно равны нулю. Моле­кулярная структура многих материалов статистически изотроп­на *), и для них коэффициент ки должен иметь такую форму, чтобы свойства материала во всех направлениях были одинако­выми. Тогда любые ортогональные оси координат должны быть главными осями коэффициента ку, а это возможно только в случае

...