Источник: Ю.П. Доронин, "Физика океана". Ленинград, гидрометеоиздат 1978
     

      В преобладающем числе случаев для практических нужд интерес представляет в различной степени сглаженный ход температуры воды, а не ее мгновенные значения. Поэтому, как уже отмечалось, проводится осреднение температуры за некоторый промежуток времени, в результате которого в уравнении теплопроводности появляются члены, зависящие от произведения пульсаций скорости и температуры. Они являются следствием математической операции осреднения. С точки зрения физики пульсации следует рассматривать как кратковременные изменения направления и скорости потока, а также связанной с ними температуры относительно неизменных в пределах осреднения значений этих гидрологических элементов. Пульсации имеют случайный характер как по повторяемости, так и по величине и продолжительности. В частности, измерения зафиксировали продолжительность пульсаций от 10-2 с до нескольких суток. Но и эти данные ограничены сверху длительностью регистрации, а снизу — чувствительностью аппаратуры.

      При рассмотрении турбулентности отмечалось, что осреднен-ное произведение пульсаций двух элементов можно представить в виде произведения коэффициента турбулентности и градиента осредненного элемента, в данном случае — температуры. Чтобы легче было проводить оценку значимости тех или иных слагаемых в уравнении теплопроводности, пока не будем заменять пульсационные слагаемые через градиент температуры и коэффициент турбулентной теплопроводности. В таком случае осред-ненное уравнение теплопроводности может быть представлено в виде

      Поскольку относительные пульсации плотности воды по крайней мере на два порядка меньше относительных пульсаций температуры, что следует из уравнения состояния, то при осреднении уравнения теплопроводности пульсации плотности во внимание не принимались.

      Ради краткости записи знак осреднения оставлен только над пульсационными слагаемыми, а все остальные элементы здесь и далее полагаются средними и неизменными в пределах интервала осреднения.

      Уравнение (4.1) характеризует изменение потенциальной температуры воды, обусловленное: а) горизонтальной адвекцией, которая определяется вторым и третьим членами левой части уравнения; б) упорядоченными вертикальными токами, выражаемыми последним членом левой части уравнения; в) фазовыми переходами и диссипацией механической энергии (QH); г) молекулярной теплопроводностью; д) лучистым потоком тепла; е) турбулентной теплопроводностью, выражаемой последними тремя членами правой части уравнения.

      Входящие в уравнение теплопроводности слагаемые весьма неоднородны по своей величине и играют неодинаковую роль в процессах различного масштаба.

      Для того чтобы оценить роль каждого члена, следует преобразовать уравнение (4.1) к безразмерному виду (с индексом «б»), воспользовавшись характерными масштабами величин (с индексом «х») по соотношениям:

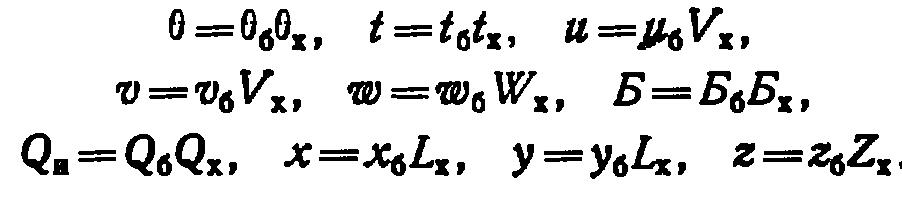
      При использовании этих соотношений уравнение (4.1) преобразуется к виду

      Поскольку безразмерные сомножители имеют величину порядка 1, то вклад того или другого члена определяется характерной величиной масштабных коэффициентов, т. е. зависит от масштаба рассматриваемого явления. А. С. Монин [12] предложил выделить семь классов процессов с соответствующими интервалами по времени.

      1. Мелкомасштабные явления с колебаниями температуры от долей секунды до десятков минут. Осреднение исходного уравнения теплопроводности было проведено таким образом, чтобы исключить рассмотрение изменений температуры воды в этом интервале времени. Поэтому уравнение (4.1) не пригодно для описания мелкомасштабных изменений температуры.

     2. Мезомасштабные явления с изменениями гидрологических элементов продолжительностью от часов до суток и с Lx~ 10 км, Zx~10 м. В преобладающем большинстве случаев для процессов такого масштаба txVxlLx~ 10"1, но в районах с большими приливо-отливными колебаниями уровня и сопровождающими их течениями этот множитель может иметь величину порядка 1. Поэтому при изучении изменений температуры моря суточного масштаба адвекцию тепла течениями можно не учитывать только в тех районах, где приливные течения не очень сильные.

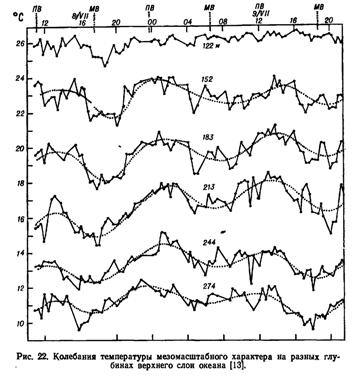
     Из-за малости характерной величины упорядоченных вертикальных токов в среднем имеем t^WxlZx^lQr2, но в районах, где отмечаются большие приливные колебания или крупные внут-' ренние волны, этот множитель может возрастать на 1—2 порядка. На рис. 22 видно, насколько существенны изменения температуры воды, вызванные ее вертикальными смещениями. Естественно, что эти колебания могут быть вычислены только в том случае, если в левой части уравнения теплопроводности присутствует третий член.

     Действие внутренних источников и стоков тепла за счет фазовых преобразований наиболее сильно проявляется на самой поверхности океана, где в результате испарения происходит понижение температуры поверхностной пленки воды. Но, как будет показано при рассмотрении теплового баланса океана, испарение представляет собой поверхностный процесс, и поэтому оно из уравнения теплопроводности исключается, а входит в качестве одного из слагаемых в уравнение теплового баланса поверхности океана, которое используется в качестве одного из граничных условий при изучении изменений температуры воды.

     Тепловой эффект других фазовых преобразований может проявляться сколь-нибудь заметным образом только при интенсивном образовании поверхностного и внутриводного льда. В первом случае тепло выделяется на нижней границе ледяного покрова, а во втором — в толще воды. В течение зимнего сезона в районах стационарных полыней Антарктики и Арктики может образовываться большая масса внутриводного льда. Отмечено, что на некоторых участках прибрежных антарктических льдов общая толщина включений внутриводного льда, накопленного за зиму, достигает нескольких десятков сантиметров и даже метра. Следовательно, при мезомасштабных процессах этот источник тепла дает вклад порядка 10~2, но с увеличением масштаба явления

     роль этого члена возрастает пропорционально продолжительности выделения теплоты кристаллизации.

     Еще меньше выделяется тепла при диссипации механической энергии. Принимая во внимание оценки этого источника энергии [9], получим, что его вклад составляет величину порядка 10-4.

      Поэтому при расчетах температуры моря диссипация механической энергии в тепловую никогда во внимание не принимается.

      Совершенно незначительна роль горизонтальной молекулярной теплопроводности в изменениях температуры воды рассматриваемого масштаба. Даже при 1Х~1 км этот член имеет величину порядка 10~8. Также мала роль молекулярной теплопроводности в переносе тепла по вертикали.

      При Zx—10 м величина этого члена имеет порядок 10~4. По сравнению с ними вклад турбулентного переноса тепла неизмеримо больше. Так, при V ~W' ~ 10-1 см/с и 6' ~ 10-1 град величина членов, учитывающих горизонтальный турбулентный перенос тепла, составляет Ю-3, а вертикальный 10° в верхнем слое океана. В глубинных слоях океана со слабым течением и малыми пульсациями температуры и скорости роль турбулентного переноса тепла сильно убывает.

      Поглощение лучистого тепла в океане довольно существенно влияет на его температуру. В пределах верхних 10 м, где происходит наиболее интенсивное поглощение коротковолно-J?*" вой радиации, этот член имеет величину порядка 10""1. На больших глубинах энергия проникшей коротковолновой радиации становится ничтожно малой, и ее влияние на изменение температу-. ры воды обычно во внимание не принимается.

      Поскольку в процессах рассматриваемого масштаба вертикальные смещения воды невелики, то для них адиабатическую поправку можно считать линейно пропорциональной глубине: 9 = = 7'(l+YaZ). в этом случае вклад адиабатических изменений температуры определится параметром

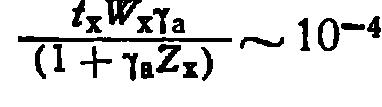
      3. Синоптическая изменчивость с периодами от нескольких суток до нескольких десятков суток. При этом пространственные масштабы процесса можно полагать Lx~102 км, Zx~5-10 м. Эта изменчивость гидрологических элементов прежде всего заключается в непериодическом формировании в океане вихрей с масштабами порядка 100 км. Изменения поверхностной температуры в районах меандров таких течений, как Гольфстрим и Куросио, могут достигать нескольких градусов. Полагают, что это основной вид изменчивости вод Мирового океана. О ее интенсивности можно судить по спектру флюктуации температуры (•рис. 23). Оценка порядков величин членов, входящих в уравнение (4.2), показывает, что t*W*IU~\, kW1iIZyi~\Qr\ т. е. горизонтальная адвекция тепла играет важную роль в изменениях температуры воды рассматриваемого масштаба. Существенно возрастает роль упорядоченных вертикальных потоков.

     Перенос тепла посредством горизонтальной турбулентности примерно на порядок меньше адвективного, и поэтому часто во внимание не принимается. Вертикальный турбулентный перенос тепла имеет величину порядка 1 и, так же как в мезомасштаб-ных процессах, играет основную роль. В поверхностном слое океана возрастает вклад радиационных изменений температуры. Величина соответствующего члена в уравнении притока тепла возрастает до значений порядка 0.1.

     Вертикальное турбулентное перемешивание, как и в рассмотренных масштабах изменчивости, является основным механизмом распространения тепла по вертикали.

...