Source: PROCEEDINGS OF WORLD ACADEMY OF SCIENCE, ENGINEERING AND TECHNOLOGY VOLUME 2 JANUARY 2005 ISSN 1307-6884, http://www.waset.org/pwaset/v2/v2-20.pdf

Grey Prediction Based Handoff Algorithm

Seyed Saeed Changiz Rezaei, Babak Hossein Khalaj

Abstract
As the demand for higher capacity in a cellular environment increases, the cell size decreases. This fact makes the role of suitable handoff algorithms to reduce both number of handoffs and handoff delay more important. In this paper we show that applying the grey prediction technique for handoff leads to considerable decrease in handoff delay with using a small number of handoffs, compared with traditional hystersis based handoff algorithms.

I. Introduction

WIRELESS communication systems are the best candidates to facilitate the communication from anywhere with any type of information, and always best connected (ABC)concept, where a person is allowed to choose the best available access networks and devices at any point in time([1], [2]). Here, the role of cellular systems becomes more important,since they are capable to enhance the network capacity significantly.
The projected market growth in personal communication network (PCN) has resulted in reduced cell sizes, over time. Cell size reduction, reduces the coverage area of the base station (BS), which means that a channel can be reused over a smaller distance with a subsequent increase in its reuse factor, and this makes handoff role really critical in future wireless networks ([2]). Traditional handoff algorithms are as follows ([3]):

1. Handoff based on Relative Signal Strength: in which the strongest received BS is selected at all times.([4])
2. Handoff based on Relative Signal Strength with threshold: in which a user hands over only if the current signal is sufficiently weak (less than a threshold) and the other is the stronger of the two.
3. Handoff based on Relative Signal Strength with hysteresis: in which a user hands over if the new BS is sufficiently stronger (by a hysteresis margin) than the current one.
4. Handoff based on Relative Signal Strength with hystersis and threshold: in which a user hands over to a new BS only if the current signal level drops below a threshold and the target BS is stronger than the current one by a given hystersis margin.
5. Handoff based on Prediction techniques: in which the handoff decision is made on the expected future value of the received signal.([5])
6. The application of nonstandard approaches to handoff mechanism such as neural networks, fuzzy logic,hypothesis testing, and dynamic programming. ([6], [7], [8])
As the cell size shrinks to increase capacity, the number of cell boundary crossings increases, and consequently the number of inter-cell handoff is also increased which is not favorable. If the aforementioned traditional handoff algorithm based on averaging is used, large averaging window and hysteresis is needed to lower the number of handoffs. However, this leads to excessive delay in handing off which consequently causes large call dropping probability. Here we show that applying the powerful grey prediction tool for handoff can minimize two contradictory parameters i.e. expected number of handoffs and handoff delay simultaneously.
This paper is organized as follows. In section 2 grey prediction is reviewed. In section 3 handoff algorithm based on grey prediction is introduced. Section 4 compares the ability of Grey prediction based handoff algorithm with that of handoff algorithm based on averaging in order to satisfy the requirements of future networks i.e. minimizing both handoff delay and number of handoffs. Section 5 concludes the paper.

II. GREY PREDICTION THEORY

Grey theory was proposed by J. L. Deng in 1982 [9]. A system is called “white” if all the information of the system is known. On the other hand, a system is called “black” if we do not know anything about it. Thus a grey system is the one which is partially known. Grey prediction power comes from its ability to predict the future value with only a few data.
Grey prediction based on grey model (GM) has three basic operations: accumulated generating operation (AGO), inverse accumulated generating operation (IAGO) and grey modeling. The GM (1, 1) model is the most commonly used model. The first 1 in GM(1,1) means that there is only one variable, and the next 1 means that the first order grey differential equation is used to construct the model.
The grey prediction algorithm based on GM (1, 1) model is as follows:
Consider the non negative data:
u⁰=[u⁽⁰⁾(1),u⁽⁰⁾(2),u⁽⁰⁾(3),...,u⁽⁰⁾(n)].
Then the GM(1,1) is: u^(k)+aZ⁽¹⁾(k)=b,k=1,2,3...,n
where "a" is called "develop parameter" and "b" is called "grey input". Now go through the following procedures:

1. Take AGO on u⁰: u⁽¹⁾(k)=AGO(u⁽⁰⁾(k))=∑u⁽⁰⁾(k)

2. Find Zu⁽¹⁾(k): Z⁽¹⁾(k)=0.5[u⁽¹⁾(k)+u⁽¹⁾(k-1)]

3.Using Least Squares Method, find matrix B and vector y_n:
y_n=[u⁽⁰⁾(2),u⁽⁰⁾(3),u⁽⁰⁾(4),..,u⁽⁰⁾(n)]

4.Estimate the parameters a and b by the following set of equations:
[a,b]^T=(B^TB)^-1B^Ty_n

5.Find the response equation:
u⁽¹⁾(k+1)=[u⁽⁰⁾(k)-b/a]e^-ak+b/a

III. GREY HANDOFF ALGORITHM

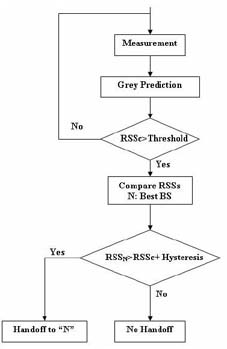
Fig. 1a depicts a traditional handoff algorithm based on averaging interval and relative signal strength with threshold and hysteresis margin. As it is shown in the figure, the Received Signal Strength (RSS) is averaged and compared with a threshold. If current RSS (RSSc) is greater than the threshold, handoff is initiated and the best BS is selected. If the RSS of the candidate BS is greater than that of the current BS plus hysteresis, user hands over to the candidate BS.
Fig. 1b shows handoff algorithm based on grey prediction. The handoff mechanism and decision making is the same as the one stated above; however, the algorithm benefits from Grey Prediction described in the previous section that replaces averaging in traditional handoff algorithms. This modification as will be further explained in the next section leads to considerable performance gain in terms of expected number of handoffs and handoff delay (two contradictory parameters in traditional handoff algorithms based on averaging).

IV. SIMULATION RESULTS

Here we assume that two base stations A and B are separated by D meters, and the mobile terminal (MT) is moving from A to B in a straight line (Line Of Sight scenario). The velocity of MT is constant and the received signal strengths from both stations are sampled at the constant interval of ds meter. The signal strengths can be calculated by the following formulae:
RSS_A(k)=Pt-10nlog(kd_s)+u(kd_s)
RSS_B(k)=Pt-10nlog(D-kd_s)+v(kd_s)
where the signal strengths (RSS_A and RSS_B) consist of transmitter power (Pt), path loss and shadow fading terms (u and v). The shadow fading terms are lognormal fading processes which are generated with a zero mean white Gaussian process passed through a single-pole autoregressive filter [10]. The autocorrelation of the filter’s impulse response is set to be
R_s(d)=σ_s²exp(-d/d₀)
where σ_s² is the standard deviation of the white Gaussian process, d₀ is the correlation distance, and d is the distance from either BS_A or BS_B.
There are several performance metrics to evaluate a particular handoff algorithm. These metrics are: call blocking probability, handoff blocking probability, handoff probability, call dropping probability, number of handoffs, and handoff delay. Here we use call dropping probability, number of handoffs, and handoff delay to evaluate and compare the performance of Grey prediction based handoff algorithm with that of traditional handoff algorithm based on averaging interval.
In a particular handoff algorithm, it is desirable to reduce number of handoffs and handoff delay (in order to reduce network’s load and call dropping probability, respectively)simultaneously. However, as it is shown in figures 2, and 3, in a traditional handoff algorithm based on averaging (with hysteresis and threshold) satisfying both requirements seems rather impossible. Fig. 2 shows that with a fix hysteresis level (=14 dB), increasing the averaging interval leads to both mean number of handoff reduction and increase in call dropping probability(Call dropping probability is the probability of RSSc to be lower than threshold value by 10dB). Furthermore, Fig. 3 shows the handoff delay of the traditional handoff algorithm by mean number of handoffs versus crossover point as hysteresis level changes from 0 to 22dB(Crossover point is the distance from BSA where the probability of assignment to BSA becomes 0.5). As it is obvious from the figure, mean number of handoff of 1 is only achieved for crossover point 1230m, i.e. a delay of approximately 230m is imposed on the system. On the other hand, by using Grey prediction based handoff algorithm, mean number of handoffs equal to 2 can be achieved without any delay (in the middle point of the 2 BS) by slight increase in hysteresis level, and 1 number of handoff is achieved in crossover point 1030m (i.e.30 meters delay).