Секция №1. «Математическая»

Гурин С.Н. Рук. Лесина М.Е.

ЭНЕРГЕТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ СОБСТВЕННОЙ ЧАСТОТЫ

        Задавая определенную форму колебаний системы с распределенными массой и упругостью, мы приписываем ей тем самым одну степень свободы (то есть одной функцией полностью определяется состояние, положения всех материальных точек системы в любой момент времени). Для определения собственной частоты колебаний такой схематизированной системы также весьма удобен энергетический способ (называемый в этом случае – методом Рэлея). Разумеется, что при этом результаты будут зависеть от выбора формы колебаний, и решение не будет обладать однозначностью. Рассмотрим наиболее общую форму метода Рэлея применительно к задаче о поперечных колебания балки. Предположим, что перемещения точек оси балки описывается законом:

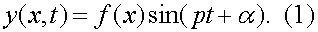
        Значит колебания всех точек оси происходят с одной и той же частотой и находятся в одной и той же фазе (то есть все точки одновременно проходят через положения равновесия, одновременно достигают наибольших отклонений и так далее). Функция f(x) представляет собой форму колебаний, то есть описывает конфигурацию изогнутой оси в момент, когда прогибы достигают максимума:

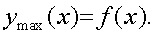
        Соответственно закону (1) скорости всех точек оси балки определяются зависимостью:

        а максимальные скорости (в момент прохождения системы через состояния равновесия) – зависимостью:

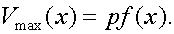
        Максимальная потенциальная энергия:

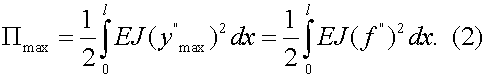
        Максимальная кинетическая энергия:

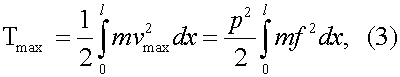
где m=m(x) – интенсивность распределенной массы балки.

        Приравняв выражения (2) и (3), получим основную формулу Рэлея для случая поперечных колебаний:

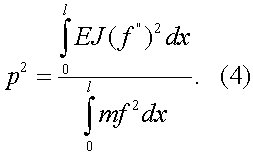
        Если кроме распределенной массы с осью балки в сечениях хi связаны также сосредоточенные грузы с массами mi , то соответственно формула (4) приобретает вид:

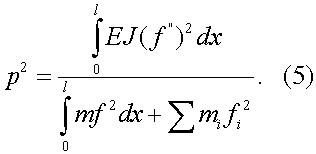
        Приведенные варианты записи формулы Рэлея дают точные результаты при условии, что в формулу подставляется истинная форма колебаний f(x). Но эта форма заранее неизвестна, и поэтому при практическом использовании формулы Рэлея задаются формой колебаний, что и вносит некоторую не точность в результаты. Рэлей не только предложил описанный способ, но и доказал важную теорему: получаемое поэтому способу приближенное значение собственной частоты всегда выше истинного значения или равно ему. Эта теорема позволяет, по крайней мере, всегда судить о знаке ошибки приближенного значения. При выборе функции f(x) ее масштаб вообще никакой роли не играет; умножение f(x) на любое число не изменит результата, как видно из структуры формулы (4). Необходимо стремиться лишь к тому, чтобы возможно лучше отразить ожидаемую форму колебаний и, во всяком случае, обеспечить выполнение граничных условий, соответствующих заданным условиям концов балки.

Список использованной литературы

1. Пановка Я.Г. Основы прикладной теории колебаний и удара. Изд.3-е, доп. и перераб. Л., «Машиностроение», 1976. – 320с.