Многие специальности технических университетов изучают знаменитую формулу Эйлера
      Даже, более того, она удобна при выводе структуры общего решения линейных дифференциальных уравнений второго порядка с постоянными коэффициентами, а эта тема, как известно, предшествует разделам «Функциональные ряды» и «Элементы функции ТФКП».
      В связи с чем полученная заранее формула Эйлера, которая обладает большой практической важностью, является актуальной задачей в учебном процессе. Отступив от традиции, когда разговор о возведении числа в мнимую степень лишен смысла, обоснуем формулу Эйлера, опираясь на формальные математические преобразования, в самом начале курса математического анализа.
      При изучении темы «Пределы» студентам хорошо известен предел, который получается из «второго замечательного предела»: который, разумеется, справедлив при любом действительном х.
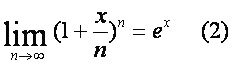
      Рассмотрим условие, полагая x=iy, где y – действительное. Получим комплексную последовательность:
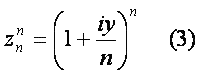
      Вначале исследуем последовательность 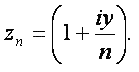Для этой последовательности 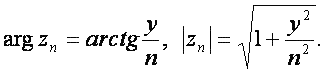Тогда для последовательности (3)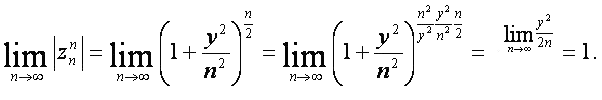
      С учетом операций с аргументом комплексного числа Выполним замену
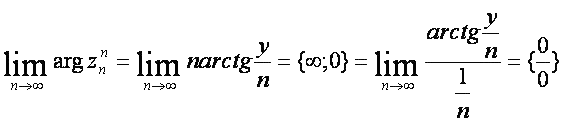
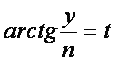
      Таким образом, пределом последовательности 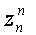есть комплексное число с модулем равным единице и аргументом y, то есть
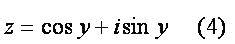
      Итак, предел последовательности 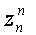существует и нам известен (4), то есть, справедлива формула (1). Примем её за значение выражения .
      Естественно, что такой подход вывода формулы Эйлера предполагает, что студенты знакомы с действиями над комплексными числами. Если этот материал не был изучен в школьном курсе по математике, то он, как правило, изучается на вводных лекциях по высшей математике на первом курсе.