Автореферат Электронная библиотека Ссылки по теме Отчёт о поиске Индивидуальное задание
Качественные показатели различных машин, механизмов, приводов и устройств являются важнейшими показателями оценки изделия в целом. Технический прогресс в любой области машиностроения связан с серьезными исследованиями, в том числе и с исследованиями прочности. Статическая и усталостная прочность является главным критерием, определяющим работоспособность машин. В данной публикации речь пой-дет о сравнении двух методик расчета: стандартной [1] и конечно-элементным анали-зом прочности зубчатых колес. Анализ проводился с использованием модулей APM Trans и APM Structure3D системы APM WinMachine, разработанной Научно-техническим центром АПМ.
Большая часть тяжело нагруженных машин, особенно горные, транспортные и др. работают при высоких нагрузках и в условиях значительного запыления окружающей среды. Тяжелые условия работы и динамический, вибрационный характер нагружения этих машин снижают прочность и время эксплуатации зубчатых передач их приводов. В связи с этим, исследования, направленные на разработку средств прогнозирования изменения качественных характеристик зубчатых передач в зависимости от нагрузки, являются актуальными и соответствуют требованиям научно-технического прогресса современного машиностроения.
Анализ показывает, что условия нагружения зубчатых передач таковы, что их расчет должен существенно отличаться от расчета передач общего машиностроения, напряженное состояние которых изучено достаточно подробно и расчет которых стандартизован [1].
Согласно этому стандарту зуб рассчитывается на изгиб как консольная балка переменного сечения. В качестве примера рассмотрен расчет на изгиб зубьев прямозубой цилиндрической передачи редуктора скребкового конвейера СП63М имеющей следующие характеристики. Модуль m=9 мм, количество зубьев шестерни и колеса z1=13 , z2=42 , соответственно, ширина зубчатого венца b1=114 мм. Частота вращения быстроходного вала n=163 мин-1, момент на быстроходном валу T1=3284 Нм. В соответствии со стандартом [1] при расчете зуба на изгиб необходимо определять напряжение σF в опасном сечении в зоне переходной кривой по следующей формуле
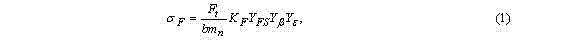
где mn - нормальный модуль (для прямозубых колес mn=m ); Yb- коэффициент, учитывающий влияние наклона зуба (для прямозубых колес Yb =1). Остальные параметры необходимо рассматривать особо. Ft- окружная сила на делительном цилиндре, которая определяется по формуле

где d1=mz1 - диаметр делительного цилиндра шестерни. Коэффициент YE , учитывающий влияние перекрытия зубьев, при указанном контакте прямых зубьев в зацеплении находится только 1 пара зубьев, YE =1. Коэффициент Yfs (формы зуба) учитывает влияние формы зуба и концентрацию напряжений, определяется по соответствующей номограмме [1]. В частности, при стандартных значениях коэффициента высоты головки зуба h*a1=1 , коэффициента радиального зазора c*=0.25 , при смещении исходного контура x=0.2 , коэффициент формы зуба шестерни Yfs =4,0 (при z1=13 ). Остается неопределенным коэффициент нагрузки Kf , который равен
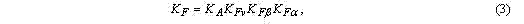
где KA - коэффициент, учитывающий внешнюю динамическую нагрузку, неучтенную в циклограмме нагружения, можно считать KA =1; Kfa - коэффициент, учитывающий распределение нагрузки между зубьями, при однопарном контакте Kfa =1. Коэффициент Kfv , который учитывает динамическую нагрузку, возникающую в зацеплении, определяется по формуле

Формула (4) применима, так как условие vz1/1000<1 , которое используется для прямозубых передач, выполняется. Здесь v - окружная скорость точек на делительном цилиндре. В формуле (4) Wfv- удельная окружная динамическая сила, которая определяется по формуле
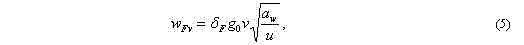
где бf - коэффициент, учитывающий влияние вида зубчатой передачи и модификацию профиля зубьев, для прямозубых передач без модификации головки бf=0,16; g0 - коэффициент, учитывающий влияние разности шагов зацепления зубьев шес-терни и колеса, при модуле и 9й степени точности go=8,2; aw- межосевое расстояние; u - передаточное число. С учетом принятых значений, коэффициент Kfb =1,03. Коэффициент Kfb предназначен для учета неравномерности распределения нагрузки по длине контактной линии. Определяется по соответствующей номограмме [1]. Для рассматриваемых колес коэффициент Kfb =1,4.
Определенное при помощи формулы (1) и всех описанных коэффициентов напряжение изгиба в опасной зоне переходной кривой равно σ=309 МПа. Такой же результат был получен и при расчете этой же передачи, выполненный с использованием модуля APM Trans.
Пакет APM WinMachine позволяет выполнить анализ напряженного состояния объектов при применении метода конечных элементов. Метод конечных элементов относится к вариационным методам теории упругости и позволяет оценивать напряженно-деформированное состояние плоских и объемных элементов конструкций.
Для моделирования напряженного состояния зуба в настоящей работе были использованы модули пакета APM WinMachine: APM Studio и APM Structure3D. Методика создания объемной модели зуба описана в работе [3].
Опорные узлы конечных элементов, связанные с ободом зубчатого колеса, закреплялись неподвижно. Разбиение модели зуба на отдельные элементы выполнялось таким образом, чтобы, во-первых, обеспечить более мелкую дискретизацию в переходных зонах у основания зуба, во-вторых, сетка выбиралась таковой, чтобы граничные узлы совпадали с точками приложения силы.
Распределенная нагрузка, разложенная на составляющие, прикладывалась в узлах линии контакта по длине зуба. Был заложен вариант нагружения, соответствующий приложению распределенной нагрузки в узлах, расположенных на делительном цилиндре по длине зуба. В первом приближении нагрузка по длине зуба считалась равномерно распределенной. Величина усилия определяется с учетом коэффициента нагрузки Kf , определяемого по формуле (3). Направлена данная сила под углом давления 20 . Вычислены окружная и радиальная составляющие данной силы: Ft=53939 Н и Ft=21268 Н, соответственно.
На рис. 1 показано распределение изгибных напряжений σF в рассматриваемом зубе при приложении указанной нагрузки.

Сравнение значений напряжений, полученных при помощи МКЭ σF=117 МПа с результатами расчета при помощи стандартной методики σF=309 МПа показывают, что стандартная методика дает почти в 2,65 раза завышенные напряжения изгиба. Это можно объяснить следующим образом: в методе МКЭ принято допущение, что напряжения в каждой точке конечного элемента одинаковы, поэтому для повышения точности метода нужно уменьшать размеры элемента, что, в свою очередь, увеличивает время расчетов и требует применения более мощных компьютеров.
Таким образом, проведенные при помощи пакета APM WinMachine исследования напряженного состояния зубьев показывают, что при проектировании передач не доcтаточно проводить расчеты с использованием стандартных методик.
Список литературы:
1. Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет на прочность. – ГОСТ 21354-87. – М.: Изд-во стандартов, 1988.
2. Сладковский А.В., Виноградов Б.В. Исследование напряженного состояния зубьев крупногабаритных передач при помощи ППП MSC/NASTRAN // Труды Российской конференции пользователей систем MSC – М.: 2000.
3. Голдобин В.А., Онищенко В.П., Пустовой А.А. Определение жесткости зуба зубчатого колеса методом конечных элементов // Машинознавство / Матеріали 8-ої регіональної науково-методичної конференції. - Донецьк: ДонНТУ, 2006. – С.34-38.
Автореферат Электронная библиотека Ссылки по теме Отчёт о поиске Индивидуальное задание