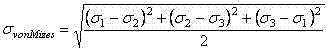
Автореферат Электронная библиотека Ссылки по теме Отчёт о поиске Индивидуальное задание
В настоящее время на шахтах Украины и за рубежом все более широкое применение получают проходческие комбайны со стреловидным исполнительным органом. Современные высокоэнерговооруженные проходческие комбайны с исполнительными органами избирательного действия при работе в сложных горно-геологических условиях подвергаются значительным динамическим нагрузкам. Это определяет высокий уровень нагрузки их базовых корпусных деталей и актуальность оценки прочности и долговечности в указанных условиях.
Характерными конструктивными особенностями этих корпусных деталей является сложная пространственная конфигурация, значительные габариты и масса, наличие значительного количества сварных соединений. Основные критерии качества таких деталей
- прочность и долговечность;
- минимально потребная металлоемкость;
- технологичность конструкции, обеспечивающая минимальные затраты на изготовление.
Для обеспечения перечисленного комплекса свойств предлагается методика, предусматривающая использование методов оптимального проектирования, основанных, в первую очередь, на установлении и анализе пространственного напряженного состояния объекта исследования.
Применение традиционных методов расчета сварных конструкций с использова-нием высоких значений коэффициентов запаса прочности и оценкой характеристик сопротивления усталости деталей по результатам испытаний стандартных образцов материалов с типичными концентраторами напряжений или уменьшенных моделей деталей для сложных конструкций приводит к значительным погрешностям при прогнозировании ресурса конструкций и излишней металлоемкости и преждевременным отказам. Наиболее совершенные современные методы расчета сварных конструкций сложной пространственной конфигурации предусматривают использование:
- МКЭ (метод конечных элементов), методов вычислительного эксперимента и имитационного моделирования нагруженности;
- статистической оценки характеристик сопротивления усталости натурных деталей;
- формирования программ ускоренных испытаний на усталость, воспроизводящих типичные случайные режимы нагружения;
- обоснованного выбора критериев предельного состояния деталей и узлов
- вероятностного подхода к назначению коэффициентов запаса прочности с учетом основных влияющих факторов;
- использования априорных статистических закономерностей нагружения и ресурса деталей.
Оценка напряженно-деформированного состояния (НДС) деталей - один из основных расчетов на квазистатическую прочность МКЭ. Особое внимание уделяется обоснованному выбору режимов нагружения и расчетных схем. Для одной и той же конструкции может быть принято несколько расчетных схем в зависимости от целей решаемой задачи.
Для получения приемлемой точности расчетов применительно к корпусным деталям проходческих комбайнов они должны включать следующие этапы.
1. Анализ типичных режимов нагружения и выявление режимов, при которых уровень НДС деталей может достигать опасных величин, на основе опыта эксплуатации и экспериментальных исследований.
2. Обоснование расчетных схем, отражающих взаимодействие системы привода исполнительного органа и системы перемещения и учитывающей существенные (на основе сформулированных допущений) нагрузки при выявленных опасных режимах нагружения.
3. Разработка конечно-элементных моделей с максимально возможным учетом особенностей геометрии конструкции, ожидаемого уровня градиентов напряжений и контактного заимодействия деталей;
4. Оценка уровня НДС конструкций с помощью алгоритмов и программ универсального программного комплекса МКЭ.
5. Определение коэффициентов запаса прочности S = σT / σi - (здесь σT - предел текучести материала детали; σi - интенсивность напряжений для высоконапряженных областей конструкции). Выявление областей, в которых расчетные значения S меньше нормативных.
6. Обоснование рекомендаций по совершенствованию конструкций методом вычислительного эксперимента с оценкой НДС нескольких предложенных вариантов на основе конечно-элементного моделирования.
Основой предлагаемой методики оценки прочности и долговечности корпусных деталей проходческих комбайнов являются расчеты на квазистатическую прочность при типичных режимах нагружения, которые основываются на современных численных методах – на методе конечных элементов (МКЭ).
Метод конечных элементов (МКЭ) в настоящее время является стандартом при решении задач механики твердого тела посредством численных алгоритмов. Алгоритм МКЭ применительно к предлагаемой методике оценки прочности и долговечности корпусных деталей проходческих комбайнов можно представить в следующем виде.
1. Производится дискретизация объема, занимаемого деталью или сборкой на элементы, или, как говорят, строится сетка конечных элементов. Для объемного тела область разбивается (в рамках функциональности применяемого пакета COSMOSWorks) на тетраэдры с гранями, аппроксимируемыми линейными (линейная зависимость от координат) или параболическими функциями координат.
2. Для пространственных конечных элементов степенями свободы являются перемещения в направлении осей локальной системы координат элемента.
3. Определяются зависимости для преобразования перемещений и углов поворота в узлах к глобальной системе координат.
4. Вычисляются матрицы жесткости конечных элементов.
5. Полученные матрицы жесткости с использованием зависимостей для перехода от локальных систем координат элемента в глобальные преобразуются в глобальную систему координат.
6. Матрицы жесткости, представленные в глобальных координатах, объединяются в глобальную матрицу жесткости.
7. Назначенные пользователем граничные условия, статические и кинематические, приводятся к нагрузкам и перемещениям в узлах, выраженным в глобальной системе координат.
8. Для каждого конечного элемента, имея перемещения (углы поворота) в узлах и аппроксимирующие функции, рассчитываются деформации.
9. На основе компонентов напряженно-деформированного состояния и параметров прочности материала (материалов) производится вычисление эквивалентных напряжений по какому-либо критерию прочности.
Назначение критериев прочности, их использование и интерпретация результатов расчета напряженно-деформированного состояния – неотъемлемые компоненты структурного анализа. Метод конечных элементов – метод трехмерного расчета, поэтому простые критерии, основанные на сравнении отдельных компонент тензоров напряжений/деформаций, имеют ограниченное применение. Исходя из этого, в качестве критерия прочности в методике принят критерий Мизеса. Критерий Мизеса (von Mises – критерий энергии формоизменения) определяет момент исчерпания несущей способности сравнением величины эквивалентного на-пряжения с пределом текучести материала. Эквивалентное напряжение σvon Mises в некоторой точке тела рассчитывают по формуле:
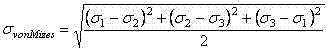
где σ 1, σ 2, σ 3 - главные напряжения.
При этом эквивалентное напряжение не зависит от ориентации площадки, на которой оно действует, то есть является инвариантным. Критерий Мизеса используется для изотропных материалов, имеющих вязкий характер разрушения. К ним относится большинство металлов, а также некоторые пластмассы, демонстрирующие помимо вязкого разрушения линейный участок на диаграмме деформирования. В пространстве поверхность прочности по критерию Мизеса описывается прямым круговым цилиндром, ось которого совпадает с пространственной диагональю, проходящей в положительном октанте системы координат главных напряжений. Их этого следует, что при всестороннем равномерном сжатии прочность материала по данному критерию бесконечна. Сечением поверхности прочности любой из плоскостей, соответствующих нулевому значению одного из главных напряжений, является эллипс, проходящий через точки и пределы прочности материала σlimit. Если это, например, плоскость σ 2 = 0, то имеет место картина, показанная на рис.1.
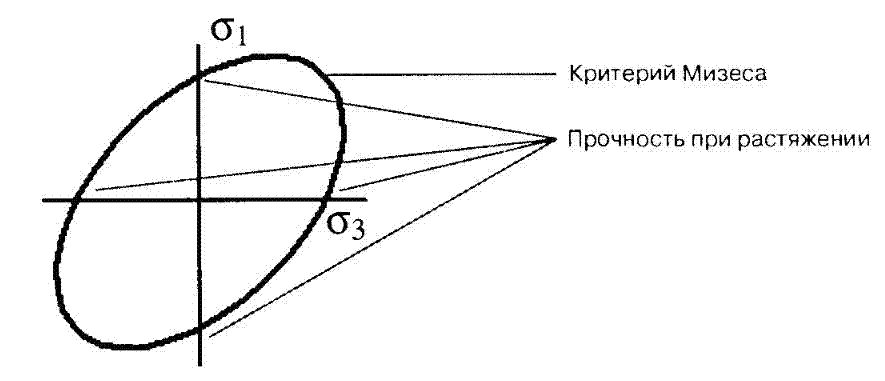
Рис.1. Эллипс Мизеса
Factor of safety (коэффициент запаса) вычисляется как отношение величины прочности (предела текучести) к максимальному, в пределах детали, эквивалентному напряжению:
Коэффициент запаса = σlimit/σvon Mizes
Пример практической реализации разработанной методики приведен на рис.2 и рис. 3.

Автореферат Электронная библиотека Ссылки по теме Отчёт о поиске Индивидуальное задание