Работоспособность деталей газотурбинного двигателя (ГТД) зависит, в основном, от качества изготовления входящих деталей и состояния их поверхностного слоя, последние направленно формируются на финишных операциях технологического процесса их изготовления [1].

        Поверхность и поверхностный слой детали с точки зрения прочности являются ослабленными. Основной причиной этого является то, что атомы на поверхности имеют устойчивые связи только с соседними и нижележащими атомами, и их состояние является неуравновешенным, неустойчивым. Кроме того, при изготовлении деталей на поверхности возникают различные микродефекты (например, микротрещины), которые при воздействии внешних нагрузок являются концентраторами напряжений.

        Разработан ряд методов, позволяющих улучшить состояние поверхностного слоя, в частности большое распространение, получили методы поверхностного пластического деформирования (ППД). При ППД наряду с упрочнением в поверхностном слое возникают благоприятные остаточные напряжения сжатия, которые оказывают положительное влияние на работоспособность узлов. Однако существует большой класс деталей, где, кроме наличия благоприятных остаточных напряжений в поверхностном слое, рабочие поверхности должны иметь специальные трибологические свойства (рабочие поверхности, посадочные поверхности, детали подвижных соединений и т.п.).

        Одним из таких методов является способ ультразвуковой упрочняющей финишной обработки (УУФО). Варьируя технологическими параметрами обработки, возможно, в определенной степени, достичь требуемых параметров качества поверхности рабочих поверхностей.

        Суть процесса сводится к следующему. Обрабатываемая деталь устанавливается в патроне токарного станка или в центрах. Ультразвуковая головка закрепляется непосредственно в резцедержателе станка (Рис.1). Далее задается частота вращения детали n (об/мин), подача S (мм/об) и усилие прижима концентратора Р (кг) к обрабатываемой поверхности.

        При ультразвуковой упрочняющей финишной обработке в поверхностном слое возникают сжимающие остаточные напряжения. Определение величин этих напряжений необходимо для того, чтобы оценить степень упрочнения поверхностного слоя и выявить, какой уровень внутренних напряжений является критическим, то есть при каких напряжениях происходит усталостное разрушение поверхностного слоя обрабатываемой детали.

        Процесс обработки сопровождается приложением внешней статической нагрузки, вызывающей упругую, а затем и пластическую деформацию поверхностного слоя. Для области упругой деформации характерно соответствие изменения напряжений и деформаций, распространяющихся в твердом теле с высокой скоростью. Внешнее воздействие сил нарушает равновесие сил взаимодействия атомов, последние смещаются в новые, более устойчивые положения. После снятия нагрузки кристаллическая решетка возвращается к первоначальному состоянию. Увеличение нагрузки вызывает большую деформацию, и начинается пластическое течение материала. Сдвигообразование в кристаллах представляет собой движение дислокаций по плоскостям скольжения и выход их на поверхность. Пластическая деформация вызывает перемещение имеющихся дислокаций, способствует возникновению новых и затрудняет их выход на поверхность.

        В зависимости от конкретных условий обработки статического давления, процессов трения, режимов обработки, теплообразования при деформации, свойств материала детали и инструмента подповерхностный максимум напряжения может располагаться на различных расстояниях от поверхности. Последнее оказывает значительное влияние на работоспособность деталей.

        Механизм формирования остаточных напряжений следует рассматривать как приближенную схему взаимодействия деформационных и тепловых процессов. При обработке каждый участок поверхности подвергается многократному воздействию деформирующего элемента, что приводит к дополнительному упрочняющему эффекту.

        Моделирование поведения тел, участвующих в процессе обработки ППД, представляет собой достаточно сложную математическую задачу. Происходит это ввиду необходимости рассмотрения в совокупности целого ряда факторов, обусловленных одновременным действием комплекса взаимосвязанных физико-механических явлений. Описание контактного взаимодействия твердых тел со сложной реологией с учетом больших деформаций, возникающих в результате процесса обработки, представляет собой основную задачу в представленной работе.

        Для решения подобной задачи требуется, наряду с определением граничных условий для тел, участвующих в контактном взаимодействии, задать реологические соотношения для всех материалов, входящих в состав контактирующих тел. В рассматриваемом случае - это материалы концентратора и обрабатываемой детали.

        Для моделирования подобных по сложности задач следует использовать численные методы, хорошо развитые и активно используемые в последнее время. При выборе конкретного метода необходимо учитывать не только эффективность самой математической процедуры вычисления, но и возможности самого программного продукта обеспечить должный уровень контроля за проведением расчета и верификационных (тестовых) испытаний.

        Всем вышеперечисленным требованиям отвечает пакет для конечно-элементного анализа ANSYS (ANSYS, Inc), который уже в течение четверти века входит в группу мировых лидеров в этой области (NASTRAN, ADAMS, LS-DYNA) и широко используется для расчетов различных конструкций. Для расчета использовалась версия ANSYS 9.

        Построение исследуемой модели соответствовало геометрическим размерам реальной контактной пары. При создании конечно-элементной модели существенное внимание было уделено разбиению области, в которой происходит непосредственное контактное взаимодействие между деформирующим элементом и обрабатываемой поверхностью, поскольку для получения адекватного решения рекомендуется использование конечных элементов, близких по форме к правильным фигурам. В рассматриваемом случае это приводит к необходимости существенного сгущения сетки элементов к поверхности контакта.

        При построении геометрической модели было решено использовать двухмерную идеализацию рассматриваемого объекта. При этом число конечных элементов (к.э.) составило около 10 тысяч. Вид конечных элементов разбиения приведен на рис. 2.

        Для моделирования процесса к инструменту прилагалась как нагрузка по оси Y (нормальная составляющая), так и сила, действующая при перемещении деформирующего инструмента по поверхности - направление оси X. Закрепление производилось заданием нулевых смещений во всех узлах, лежащих на соответствующей поверхности. На рис. 2 представлены только те области конструкции, которые непосредственно участвуют в контактном взаимодействии. Ввиду осевой симметрии для обрабатываемого тела при выборе опции "вид напряженного состояния" активизировался вариант "осесимметричное напряженное состояние". Для деформирующего инструмента выбирался вариант "плоское напряженное состояние".

        Зависимость "напряжение-деформация" для материала можно описать билинейным законом. Коэффициент Пуассона принимался равным 0,3. Величина коэффициента трения была определена экспериментальным путем, и его значение принимались в расчете в зависимости от величины нормального давления [2].

        Контактное взаимодействие приводит к значительным неравномерностям в распределении напряжений, что в свою очередь требует построения соответствующей сетки конечных элементов - в зоне с высоким значением градиента напряжений следует генерировать более мелкие конечные элементы. Следует отметить, что все элементы, в том числе и в зоне наибольшего сгущения, имеют форму, близкую к квадрату, что имеет важное значение для сходимости вычислительного процесса.

        Моделирование контактного взаимодействия в процессе нагружения проводилось с использованием контактных элементов CONTAC48, CONTAC171, CONTAC172 и TARGET169 [3]. Рассматриваемое контактное взаимодействие моделировалось как упругопластическое тело - упругопластическое тело.

        Общее количество элементов составило более 10000.

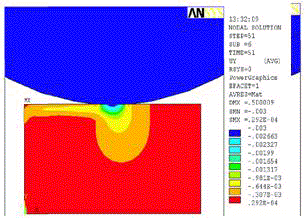
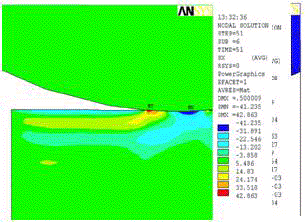
        Напряженно-деформированное состояние рассматривалось при единичном взаимодействии концентратора и стержня с плоским торцом. Материалы шарика и стержня соответствуют натуральным. При расчете используются свойства материалов при температуре 20 °С. В качестве граничных условий, использовалось следующее – шарик внедряется в стержень с начальной скоростью, перпендикулярно плоскому торцу стержня. При взаимодействии шарика со стержнем наглядно воспроизводятся характерные стадии соударения твердых тел. Получено распределение полей напряжений и деформаций, как в текстовой, так и в графической форме. Результаты расчетов напряженно-деформируемого состояния в момент времени сразу после нагружения представлены на рис. 3-5. На рис. 3 приведено распределение вертикальных смещений в зоне контакта. На рис. 4 приведено распределение касательных напряжений, а на рис. 5 приведено распределение нормальных контактных напряжений.

        Проведенный конечно-элементный анализ для предложенного способа обработки позволяет смоделировать достаточно сложные процессы, происходящие при контактном взаимодействии деформирующего инструмента и обрабатываемой поверхности, что позволит на основе технических характеристик упрочняющей установки и требований к параметрам поверхностного слоя оптимизировать технологические режимы обработки.

        Разработанная модель распределения упрочнения по обрабатываемой поверхности позволила определить время упрочнения. По рисункам 3-5 можно увидеть, что в поверхностном слое формируются остаточные напряжения сжатия, распространяющиеся на определенную глубину.

        Экспериментальная проверка показала высокую эффективность метода ультразвуковой упрочняющей финишной обработки рабочих поверхностей.