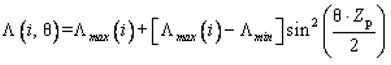
Источник: Материалы Всеукраинской научно-технической конференции студентов. – Донецьк, ДонНТУ – 2009.
Вентильные реактивные двигатели (ВРД) обладают определенными преимуществами по сравнению с другими типами электрических машин. К ним относят простоту конструкции, высокие надежность и регулируемость. Это обуславливает расширение области применения ВРД и внимание к ним со стороны разработчиков.
Для исследования характеристик ВРД широко применяется математическое моделирование. Выделяются два подхода в методах определения характеристик магнитной системы двигателя и их описании. В рамках первого подхода используется анализ схем замещения магнитной системы двигателя [1]. Основываясь на допущении о равномерности распределения индукции по поперечному сечению отдельных участков магнитной цепи двигателя, данный подход не позволяет достичь высокой точности расчета, т.к. не учитывает локальное насыщение зубцовой зоны. Весьма перспективным является второй подход, предполагающий расчет магнитной системы ВРД полевым методом, в частности методом конечных элементов (МКЭ).
Математическое описание характеристик магнитной системы также играет весьма важную роль. В этом отношении выделяется два направления. В рамках первого используют процедуру сплайновой интерполяции [2]. Недостаток данного подхода заключается в том, что он ограничивает возможность аналитического анализа процессов электромеханического преобразования энергии в ВРД. В рамках второго направления используется аналитическое описание полученных характеристик.
С помощью МКЭ в плоскопараллельной постановке задачи расчета магнитного поля было получено семейство кривых проводимостей магнитной системы ВРД мощностью 130 Вт, которое показано на рисунке 1 а в виде поверхности. Эта поверхность наглядно иллюстрирует изменение магнитной проводимости в функции двух переменных: тока и угла положения ротора.
Для аппроксимации этих зависимостей использовалось выражение, основанное на косинусоидальном изменении магнитной проводимости от угла положения ротора:
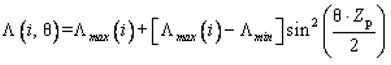
где Λmax(i) - зависимость проводимости магнитной системы для согласованного положения
полюсов статора и ротора от тока фазы;
Λmin - минимальное значение проводимости, соответствующее рассогласованному положению полюсов статора и ротора;
θ - угол между осями полюсов статора и ротора;
Zр - количество полюсов ротора.
Зависимость Λmax(i) аппроксимировалась выражением:

где Ψ1, I1 - потокосцепление и ток соответственно в точке сопряжения линейного и
нелинейного участков аппроксимируемой кривой намагничивания для согласованного положения полюсов статора и ротора;
w - количество витков в обмотке фазы ВРД;
a1, a2 - коэффициенты аппроксимации;
i - ток фазы ВРД.
В соответствии с теорией электромеханического преобразования энергии получено аналитическое выражение для электромагнитного
момента ВРД:

На рисунке 1 б приведены кривые электромагнитного момента для рассматриваемого двигателя, рассчитанные по выражению (1) (показаны сплошными линиями), а также отмечен электромагнитный момент, полученный с помощью тензора натяжения в программе FEMM (показан штриховыми линиями).
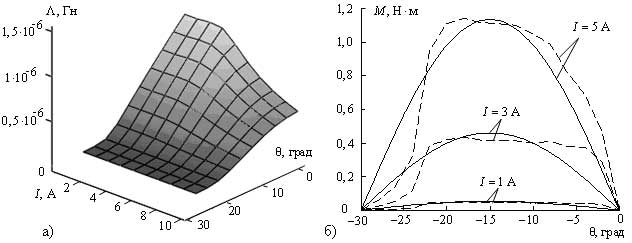
Рисунок 1 – Поверхность проводимостей магнитной системы (а) и зависимость электромагнитного момента от угла положения ротора (б)
Из рисунка 1 б видно, что точность аппроксимации ухудшается при углах положения ротора близких к согласованному и рассогласованному положениям. Это объясняется тем,
что реальная форма кривых проводимости отличается от косинусоидальной. Выражение (1) позволяет вычислять статический электромагнитный момент ВРД и может применяться
при оптимизации энергетических процессов за цикл коммутации.
Перечень ссылок
1. Bekkouche B., Chaouch A., Mezari Y. A switched reluctance motors analyse using permeance network method // International Journal of Applied Engineering Research, 2006. Vol. 1, No. 2. P.137-152.
2. Кузнецов В.А., Матвеев А.В. Дискретная математическая модель вентильно-индукторного двигателя // Электричество. 2000. № 8. - С.22-27.