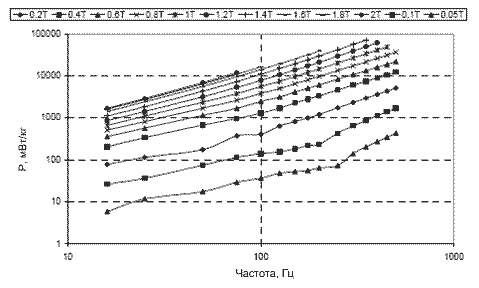
Рисунок 16 – Потери в стали при синусоидальном возбуждении

Однако распределение индукции и магнитного потока в статоре и роторе ВРД несинусоидальное. В [14] описан метод оценки потерь в стали ВРД с использованием наложения гармонических составляющих индукции. При этом используется упрощенный графический метод для получения периодических кривых индукции в различных частях машины (ярмо ротора, полюс ротора, ярмо статора, полюс статора), разложение в ряд Фурье для отдельных составляющих. Наложение потерь в стали для каждой частоты позволяет оценить полные потери в стали.

Упрощенный графический метод определения кривых индукции негибкий и неточный. Большое количество параметров управления (угол включения, угол отключения) оказывают влияние на кривые индукции в полюсах и ярме статора и ротора. При прямом сопряжении между конечно- элементной моделью и моделью привода кривые индукции могут быть рассчитаны для каждой точки. Это реализовано интегрированием ЭДС одновитковой катушки, размещенной на полюсе статора, ярме статора, полюсе ротора и его ярме (рис. 17). Индуцированное напряжение e_coil возвращается в Matlab/Simulink для расчета индукции B по выражению:

B = (1/A)∫e_coildt                (8)

где A - площадь поверхности, охватываемой катушкой.

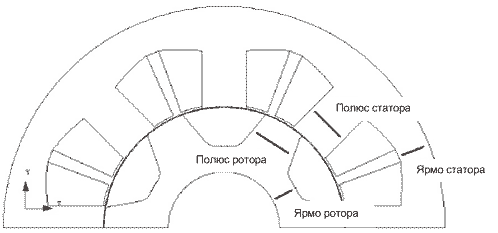
Рисунок 17 – Одновитковые катушки в МКЭ для расчета потерь в стали

Большое преимущество прямого сопряжения заключается в том, что значения индукции могут быть рассчитаны в любой точке геометрии ВРД даже при сложном алгоритме управления.

На рис. 18 показана сопряженная электрическая цепь для расчета фазных токов и индуцированных напряжений в одновитковых катушках. Кривые индукции в различных частях машины показаны на рис. 19. Спектр гармоник в кривой индукции для полюса статора показан на рис. 20. Затем выполняется суммирование потерь для каждой гармоники для определения полных потерь в стали.

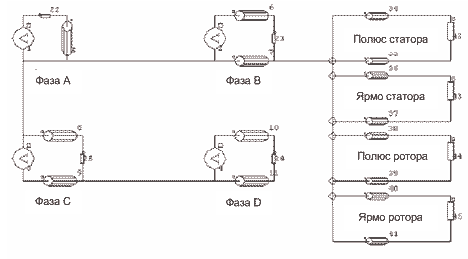
Рисунок 18 – Сопряженная электрическая схема в МКЭ для вычисления потерь в стали

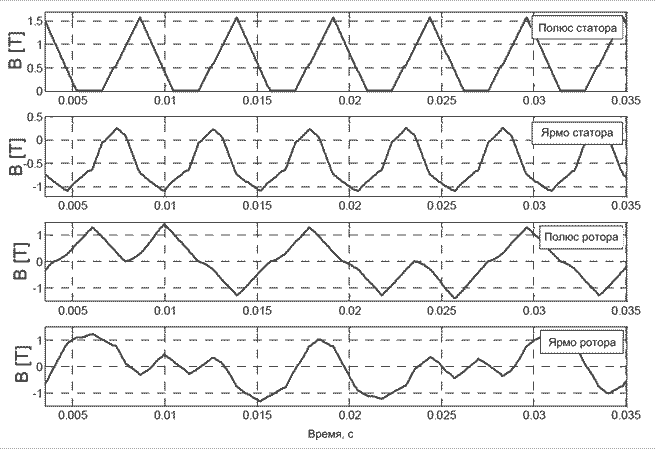
Рисунок 19 – Кривые индукции в различных частях ВРД (i=10 A, ω = 200 рад/с)

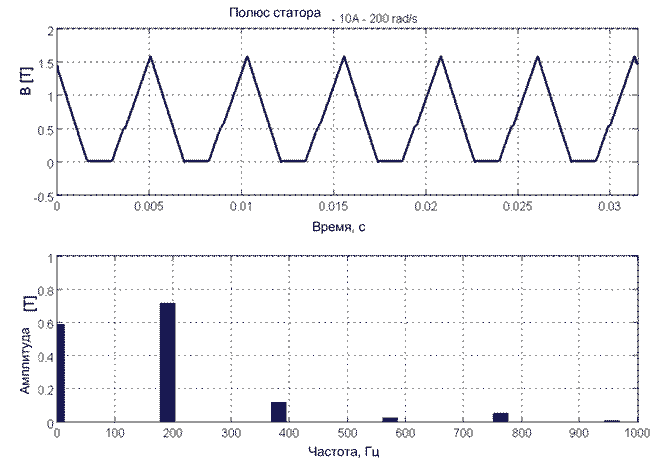
Рисунок 20 – Гармонический анализ индукции в полюсе статора (i=10 A, ω = 200 рад/с)

Для подтверждения правильности оценки потерь в стали должно быть выполнено измерение электрических потерь, механических и Джоулевых. Тогда потери в стали могут быть рассчитаны с использованием выражения (9):

P_Fe = P_el - P_mech - P_Joule                (9)

Потери в стали малы по сравнению с электрической и механической энергией. Это может привести к ошибке в оценке потерь в стали до 20%. По этой причине точное измерение потерь в стали весьма сложно. На рис. 21 приведено сравнение результатов моделирования с помощью сопряженного КЭ анализа и измерений. Погрешность вычислений составляет менее 15%.

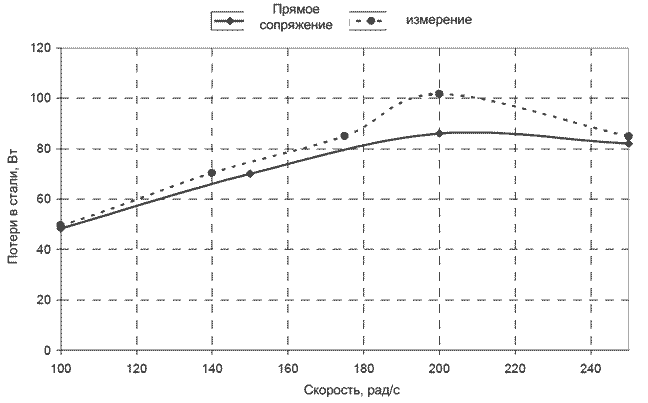
Рисунок 21 – Оценка потерь в стали (i=5 A)

С использованием информации о потерях в стали моделировались механические характеристики и сравнивались с измеренными (рис. 22). С учетом потерь в стали точность в оценке механических характеристик выше.

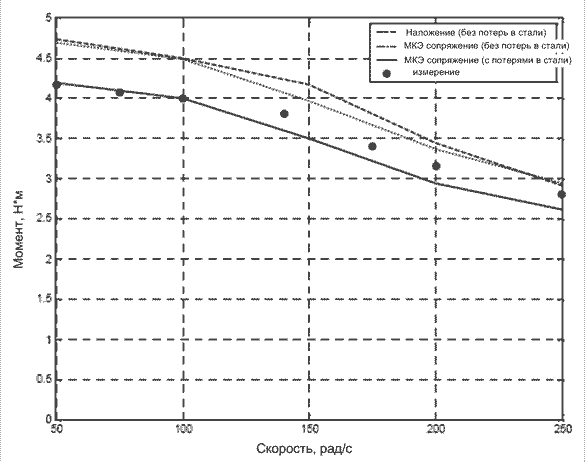
Рисунок 22 – Механические характеристики (i=5 A)

Вверх