|
|
Задача оценки ЭМС, склонной к появлению случайных шумов и инертности объекта - в расчетах квадратирования и сглаживания.
Это показывает, что распределение случайного процесса меньше, после квадратирования и сглаживания бэта - распределения.
Решение проблемы проиллюстрировано на примере оценивания допустимой несимметрии напряжения.
1.ФОРМУЛИРОВКА ЗАДАЧИ
Динамическая EMC-модель объекта обычно включает линейный фильтр, квадратирующий
и сглаживающий (СС) единицы и статистические единицы анализа: например фликерметр (IEC, Публикация 868, 1986). Фильтр
симулирует реакцию y(t) на беспокойство шума единица СС принимает во внимание факт, что результат нарушения EMC зависит
от появления реакции и инертности объекта. Мы условно сошлемся на ординаты процесса  после СС как дозы (по аналогии к дозе Фликера). Отношение между процессами до и после СС описано дифференциальным
уравнением
после СС как дозы (по аналогии к дозе Фликера). Отношение между процессами до и после СС описано дифференциальным
уравнением
 (1) (1)
где T - это константа времени инертности объекта.
Суть проблемы состоит в определении плотности распределения  или
функции распределения или
функции распределения  , на основании которой вычисляется значение пика дозы , на основании которой вычисляется значение пика дозы
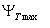 (эксцесс (эксцесс 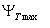 возможен с данной вероятностью Ex). Правая часть уравнения
обычно нелинейная, таким образом, точное решение существует только для специального случая телеграфного сигнала. Приближенное
решение в расширенной форме серий Edgeworth известно, но необходимая начальная информация недосягаемая на практике. возможен с данной вероятностью Ex). Правая часть уравнения
обычно нелинейная, таким образом, точное решение существует только для специального случая телеграфного сигнала. Приближенное
решение в расширенной форме серий Edgeworth известно, но необходимая начальная информация недосягаемая на практике.
Статистическое решение проблемы СС методами симуляции (синтетические пробы) предоставлено
в этом отчете. Для краткости рассматривается элементарная ЭMC-модель без фильтра, когда y = x. В этих случаях принимается
непрерывное значение стандартизированного беспокойства шума [y], и целью его изучения является определение "инерционного
максимума"  . Требование ЭМС: . Требование ЭМС: 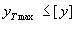 . .
Оценочное значение дозы вычисляется по принятой вероятности Ex его эксцесса решением
уравнения
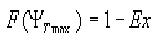 (1) (1)
В стандартах качества электрической энергии в странах СНГ, принято значение Ex = 0,05. Так как объекты с разной константой
времени инертности могут быть соединены с сетью электроснабжения, зависимость инерционного максимума от T нужно получить
в общем.
2. СИМУЛЯЦИЯ ДОЗЫ
Существуют различные методы для симуляции случайных процессов. В системах электропитания,
которые включают в себя группу источников беспокойства шума, целесообразно использовать суммирование индивидуальных беспокойств
шума со случайными изменениями. Когда осуществление достигает закона нормального распределения, любое осуществление y(t)
формируется суммой большого числа «элементарных» процессов (n = 100.. 1000) в простой форме. Элементарный процесс имеет
среднее значение, равное нулю и корреляционную функцию (КФ), в n раз меньше, чем желаемый KФ
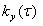 симулирующего процесса. Среднее значение y процесса y(t) прибавляется к y(t) после
суммирования элементарных процессов и перед операцией квадратирования. симулирующего процесса. Среднее значение y процесса y(t) прибавляется к y(t) после
суммирования элементарных процессов и перед операцией квадратирования.
Чтобы определить статистические решения, необходимо симулировать ансамбль большого
числа N осуществлением процесса y(t). На рис. 1 показан образец 5 из N = 500 реализаций нормального процесса отрицательной
последовательности изменения напряжения со средним значением y = l,6%, средним квадратичным отклонением
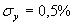 и экспоненциальной функцией корреляции со временем корреляции и экспоненциальной функцией корреляции со временем корреляции
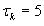 с. с.
Любая реализация y(t) – это квадратирование, и соответствие реализации дозам вычисляется,
используя интеграл Дюамеля:
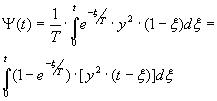 (2) (2)
где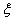 , это переменная интеграции. , это переменная интеграции.
На практике, скоротечность подходит к концу в течение времени tp=(5-6) T . Когда по типу задачи,
достаточно вычислить только функцию распространения, симуляция остановится перед t=-t p. Если, кроме того, необходимо вычислить
КФ доз по ряду аргументов от 0 до  , тогда время симуляции равно , тогда время симуляции равно
 На рис. 1б, показано пять реализаций доз за T = 10 S. Реализация доз соответствуют реализации на рис. 1а.
На рис. 1б, показано пять реализаций доз за T = 10 S. Реализация доз соответствуют реализации на рис. 1а.
Как методы симуляции обеспечивают новые знание, так и требования для качества симуляции
должны быть больше, чем для обработки экспериментальных данных. Также необходимо принять во внимание то, что действие
квадратирования увеличивает погрешность. Таким образом, необходимо добавить к проверке достоверности репродукции функции
распределения и КФ процесса y(t), необходимо проверить репродукцию функции распределения процесса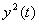 ,
который может быть определен аналитически от f(y) или F(y). . Дополнительная проверка в T = 0 гарантирует качество симуляции доз в
T > 0, так как сглаживает погрешность. ,
который может быть определен аналитически от f(y) или F(y). . Дополнительная проверка в T = 0 гарантирует качество симуляции доз в
T > 0, так как сглаживает погрешность.
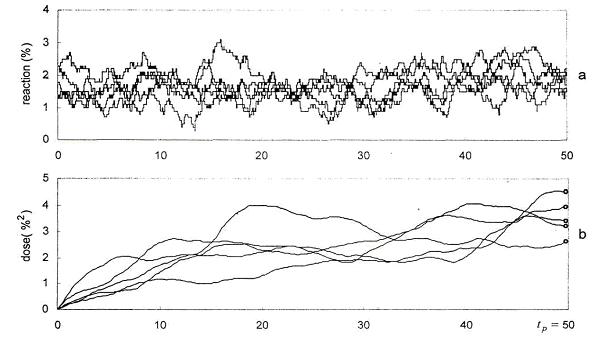
Время(секунд)
Рисунок1.
|
|