Источник информации: Изв. АНСССР, Энергетика и транспорт, 1977, № 5 – с. 128 – 140.
Рассматриваются способы моделирования нормальных процессов в электрических сетях, обеспечивающих нужную точность на участках ограниченной длительностью или частично заданной корреляционной функции.
Сравниваются характеристики и микроструктуры моделей. Выясняется необходимость использования относительных единиц. Указываются способы определения минимальной длительности моделируемых процессов.
Нормальный случайный процесс является распространенной математической моделью изменения во времени тока и напряжения в электрических сетях [1]. Одно из достоинств такой модели – возможность применения простого аппарата корреляционной теории [2]. Аналитические методы позволяют рассчитывать характеристики пиков, выбросов и колебаний без построения реализаций процессов, однако они не всегда достаточны для решения задач электроснабжения, особенно нелинейных: регулирования напряжения [3], реактивной мощности, применения стабилизаторов, компенсаторов, релейных устройств.
Поэтому в ряде случаев возникает необходимость в моделировании реализаций нормальных процессов, по которым затем определяются нужные характеристики. Существующие методы моделирования (например, [9,10]) не исчерпали всех возможностей имитации реальных процессов, на что особо указано в [10]. Рассматриваемые методы специально приспособлены для воспроизведения закона распределения и корреляционной функции (КФ) K(τ) на участках ограниченнй длительности.
В зависимости от объема исходной информации будем различать два типа задач моделирования: когда КФ задана полностью или когда она известна только для малых значений аргумента τ. Первая задача решалась в [11] только для марковского процесса с экспоненциальной КФ, в то время как интерес представляет и КФ другого вида. Метод [12] решения второй задачи не предусматривал возможности задания нескольких значений КФ и не обеспечивал воспроизведения закона распределения на заданном промежутке времени. В обоих случаях моделирование выполнялось в именованных единицах, что сужало область применимости получаемых реализаций процессов.
Для определенности изложение далее ведется в основном применительно к актуальной для практики задаче моделирования графиков нагрузки I(t) дуговых сталеплавильных печей в периоды расплавления, имеющих экспоненциально-косинусную КФ [13, 14]. Попытка решения такой задачи была предпринята в [15], где был применен метод «квантования времени» [12].
В статье рассматриваются стационарные процессы. Реализации нестационарных процессов можно разбивать на несколько «зон стационарности», в пределах которых нестационарность практически не сказывается на результатах. Прибавление или вычитание среднего значения процесса не изменяет вида КФ, поэтому при моделировании достаточно получать реализации с нулевым средним значением, т. е. реализации центрированных процессов.
При одном и том же законе распределения вид КФ зависит от порядка следования ординат процесса. В качестве максимальной модели в [1] принят марковский процесс с КФ вида
где σ – стандарт, α – величина, обратная времени корреляции. Такой процесс отличается отсутствием периодичности в изменении ординат и затухания корреляционных связей.
Противоположной математической моделью является процесс с периодической КФ, который имеет строго периодические реализации. Например, совокупность синусоидальных графиков со случайным сдвигом s, амплитудой A и длительностью цикла tц характеризуется КФ
где β=2π/tц – угловая частота.
Процессы в действующих сетях промышленных предприятий занимают промежуточное положение между предельными случаями нецикличного и периодического процессов, так как при установившемся ритме производства имеется некоторая периодичность в работе отдельных приемников, но за счет различных случайных факторов она не является детерминированной (за исключением полностью автоматизированных линий). Поэтому интерес представляет моделирование процессов с КФ
Даваемые формулами (1) и (3) КФ при τ→∞ стремятся к нулю, вследствие чего соответствующие процессы являються не только стационарными, но и эргодическими, которые можно моделировать одной достаточно продолжительной реализацией. Минимальная длительность TM реализации выбирается, прежде всего, из условия ограничения дисперсии КФ [4]:
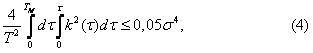
где учтено, среднее значение процесса равно нулю.
Подставив (3) в (4), с некоторым запасом получим

Заметим, что для процесса с КФ вида (1), когда β=0, минимальная длительность составляет 40 времен корреляции; для периодических реализаций, когда α=0, формула (5) не применима.
Условие (4) исключает возможные случайные отклонения получаемой КФ от теоретической в предположении, что обрабатываемая реализация заведомо имеет заданную КФ. В зависимости же от выбранного метода моделирования возможны дополнительные ограничения.
С практической точки зрения желательно строить модели процессов в относительных единицах (о. е.) с тем, чтобы одну и ту же реализацию использовать для решения различных задач, изменяя лишь масштабы осей координат. В качестве базисных величин примем стандарт и величину α. Например, в о. е. КФ (3) запишется в виде (∗ - символ о. е.)
где τ∗=ατ, β∗=β/α.
Известно, что при суммировании n не зависимых процессов их КФ складываются, а вероятностное распределение с увеличением n приближается к нормальному. Это позволяет моделировать нормальный процесс I(t) с заданной КФ в виде суммы n «элементных» процессов i(t) с одинаковыми КФ:
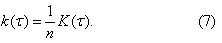
Несмотря на количество моделируемых процессов, существенное упрощение достигается за счет того, что вероятностное распределение каждого элементного процесса может быть достаточно простым, лишь бы они имели нужную КФ. В частности, в качестве элементарных удобно выбирать знакопеременные импульсные процессы с прямоугольной формой импульсов единичной величины, так как их моделирование сводиться только к воспроизведению длительностей импульсов с заданными распределениями.
Распределение суммы импульсных процессов является биноминальным [16], симметричным при одинаковых средних значениях случайных величин длительностей положительных tв и отрицательных tо импульсов. Поэтому для улучшения сходимости такого распределения к нормальному помимо большого n целесообразно принимать эти значения одинаковыми. При этом вероятности появления импульсов разных знаков будут равны 0,5, что отвечает такому же значению коэффициента включения kв нецентрированного импульсного процесса.
Виды КФ импульсного процесса зависит от вероятностных распределений длительностей импульсов. Возможны два предельных случая: эти распределения являются показательными или выражаются δ-функциями (длительности постоянны). В первом случае элементные процессы будут нецикличными, а их сумма даст КФ вида (1) с параметрами
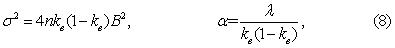
где B – величина импульсов разного знака, λ – интенсивность (средняя частота) появления импульсов.
Приняв kв=0,5, заключаем, что моделирование нормального процесса с экспоненциальной КФ сводится к суммированию большого количества (практически n≥10) нециклических импульсных процессов (рис. 1, а) со следующими величинами и интенсивностями импульсов:
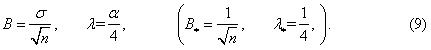
КФ вида (1) может быть также получена суммированием процессов с экспоненциальной (рис. 1, б), а не прямоугольной формой импульсов, имеющих тот же закон перемены знака (пунктир на рис. 1, б).

Во втором случае моделирование периодических элементных процессов – импульсных или синусоидальных (рис. 1, в, г) – осуществляется очевидным образом. Их суммирование производится со случайными сдвигами s, равномерно распределенными в пределах длительности цикла tц. Суммарный процесс не обладает свойством эргодичности, поэтому при моделировании требуется большое количество реализаций (практически 40 – 50), но длительностей всего tц.
Заметим, что при цикличных элементных процессах с постоянной длительностью импульсов одного знака и показательным распределением импульсов другого знака и показательным распределением импульсов другого знака (рис. 1, д) нормальный процесс имеет убывающую до нуля по прямолинейному закону КФ (τ≤kв/λ)
или с учетом (8) в о. е.
Перейдем к рассмотрению процессов с экспоненциально-косинусной КФ. Сама структура формулы (6) определяет путь поиска элементных процессов для случая. В самом деле, известно, что КФ произведения независимых центрированных процессов равна произведению их КФ. Это позволяет в качестве элементного процесса (рис. 1, е) выбрать произведение двух процессов: нецикличного и периодического (штриховая линия). С учетом (2) и (8) найдем формулы для характеристик этих процессов при kв=0,5:
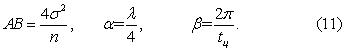
Ввиду неоднозначности формулы для A и B необходимо задаваться любой из этих величин. Тогда ординаты полученной реализации будут отличаться от искомых .
Таким образом, моделирование нормальных процессов с КФ вида (6) заключается в следующем: независимо друг от друга моделируются импульсные процессы с единичной величиной импульсов, затем каждая из реализаций этих процессов умножается на sin β(t+s) со случайным сдвигом s и, наконец, полученные произведения процессов суммируются. Следует подчеркнуть принципиальную необходимость использования здесь центрированных нециклических и периодических процессов, поскольку формула для КФ произведения процессов с ненулевыми средними значениями кроме произведения КФ содержит слагаемое с множителями в виде квадратов средних значений. Поэтому КФ произведения нецентрированных нециклического и периодического процессов будет отличаться от (6).
1. С. Д. Волобринский, Г. М. Каялов, П. Н. Клейн и Б. С. Мешель. Электрические нагрузки промышленных предприятий, «Энергия», 1971.
2. А. А. Свешников Прикладные методы теории случайных функций. – М.: Наука, 1968.
3. Э. Г. Куренный, И. С. Войтюк, П. Р. Никифоров. Исследование эффективности автоматических регуляторов напряжения. В сб. «Электроэнергетика и автоматизация промышленных установок». Донецк, Изд-во ДПИ, 1974.
4. Э. Г. Куреннвый, Л. В. Брусенцов. Моделирование групповых графиков электрической нагрузки методом Монте-Карло. Изв. Вузов. Электромеханика, 1968, № 7.
5. П. Р. Никифоров, Г. Г. Кочергина. Применение метода Монте-Карло для оценки колебаний напряжения. В сб. «Оптимизация режимов систем электроснабжения промышленных предприятий». Моск. Дом научно-техн. Пропаганды им. Ф. Э. Дзержинского, 1973.
6. В. Я. Потапенко. Применение вероятностного и статистического моделирования к расчету реактивных нагрузок промышленных предприятий. Изв. Вузов. Электромеханика, 1967, № 1.
7. Э. Г. Куреннвый. Моделирование суммы импульсных случайных процессов (на примере графиков нагрузки заводских электрических сетей). Изв. Вузов. Электромеханика, 1967, № 10.
8. Ю. Л. Мукосеев, Г. Я. Вагин, Е. М. Червонный. Расчет суммарной нагрузки машин контактной сварки методом статистического моделирования на ЦВМ. Электричество, 1972.
9. Д. И. Голенко. Моделирование и статистический анализ псевдослучайных чисел на электронных вычислительных машинах. «Наука»
10. И. М. Соболь. Численные методы Монте-Карло. – , 1965.М.: Наука, 1973.
11. Э. Г. Куренный. Моделирование графиков электрической нагрузки электрических сетей. В сб. «Применение математических методов и вычислительных машин в энергетике». Кишинев, Изд-во АН МССР, 1968.
12. Э. Г. Куренный. Моделирование графиков электрической нагрузки «квантованием времени». ). Изв. Вузов. Электромеханика, 1969, № 2.
13. А. М. Санаев. Исследование графиков электрической нагрузки дуговой сталеплавильной печи. «Сб. статей кафедр электрические станции, сети и системы и электроснабжение промышленных предприятий и городов Донецкого политехнического института», Киев, Изд-во МВ и ССО УССР, 1970.
14. С. В. Алексеев, В. Г. Трейвас. Статистические характеристики токов дуг дуговых сталеплавильных печей. ). Изв. Вузов. Электромеханика, 1971, № 1.
15. М. Махамед. Применение метода «квантования времени» к моделированию электрической нагрузки дуговых печей. В сб. «Электроэнергетика и автоматизация промышленных установок». Донецк, Изд-во ДПИ, 1974.
16. Э. Г. Куренный, Е. Н. Дмитриева. Расчет импульсных процессов в сетях электроснабжения. Изв. АН СССР. Энергетика и транспорт, 1972, № 3.
17. Э. Г. Куренный. К определению колебаний электрической нагрузки. Электричество, 1972, № 2.
18. Э. Г. Куренный. Метод расчета характеристик колебаний стационарных случайных процессов в заводских сетях. Изв. АН СССР. Энергетика и транспорт, 1971, № 6.
19. Э. Г. Куренный, Е. Н. Дмитриева, А. М. Санаев. О необходимости уточнения стандарта на качество электроэнергии. Промышленная энергетика, 1972, № 2.