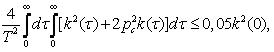
Источник информации: Изв. Вузов. Электромеханика, 1968, № 7 – с. 788-791
Групповые графики электрической нагрузки при установившемся режиме работы промышленного предприятия представляют стационарные случайные процессы [1]. Современные методы расчета пиков и колебаний электрической нагрузки [2, 3] позволяют определять детерминированные характеристики этих процессов – в первую очередь вероятностные законы распределения и корреляционные функции, по которым оцениваются величина, длительность и частота пиков и колебаний нагрузки. Однако дальнейшее использование этих величин для расчета электрических сетей по потере и колебаниям напряжения вызывают определенные трудности, связанные с необходимостью математического исследования преобразований случайных процессов нелинейными элементами (генераторами, стабилизаторами, релейной автоматикой и т. п.).
В подобных случаях, особенно при небольшом числе приемников с резкопеременными графиками нагрузки, целесообразно перейти от аналитического решения к моделированию протекания физических процессов, что требует, естественно, и моделирования этих случайных изменений. Между тем, существующие методы моделирования случайных процессов [4] воспроизводят лишь их одномерные законы распределения корреляционные функции, что ограничивает их применимость линейными системами.
В настоящей работе предлагается метод моделирования групповых графиков нагрузки (активной или реактивной), основанный на идее метода Монте-Карло [5], и дается описание устройства, автоматизирующего процесс моделирования.
Реализации группового графика получаются путем суммирования записей индивидуальных графиков нагрузки, сдвинутых друг относительно друга случайным образом. В общем случае требуемое количество таких случайных наложений, а следовательно, и реализаций, может быть достаточно большим. Известно, однако, что любая реализация индивидуального графика, записанные за длительный промежуток времени, полностью представляет сам этот график, а характеристики этих реализаций одинаковы и не зависят от момента начала записи [1]. Это свойство эргодичности позволяет ограничиться при моделировании лишь однократным наложением индивидуальных графиков с любыми начальными сдвигами между ними, что существенно упрощает сам процесс моделирования. Получаемая при этом одна реализация группового графика также обладает свойствами эргодичности и может быть использована для выбора элементов сети электроснабжения.
Необходимое время длительности записи реализаций графика нагрузки p(t), имеющего среднее значение pc и корреляционную функцию k(τ), определяется из условия [6]
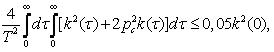
где через T обозначена длительность записи графика.
Большой практический интерес представляет обычный для проектирования случай, когда расчетные индивидуальные графики являются циклическими (прокатные станы, рудно-термические печи и др.). Если циклы таких графиков несоизмеримы, то ясно, что для моделирования группового графика достаточно одного наложения индивидуальных графиков. Для того, чтобы полученная таким образом реализация отражала все свойства группового графика достаточно одного наложения индивидуальных графиков. Для того, чтобы полученная таким образом реализация отражала все свойства группового графика, необходимо, чтобы она имела длительность T≥50 tцм (в 50 раз превышающую время tцм наибольшего цикла [6]).
В том случае, когда циклы индивидуальных графиков соизмеримы, то реализация группового графика для одного случайного наложения будет периодической, с периодом, равным общему наименьшему кратному индивидуальных периодов. Поэтому, если общее наименьшее кратное превышает длительность 50 наибольших циклов, то достаточно лишь одного наложения индивидуальных графиков. Если же это условие не выполняется, то число наложений, а следовательно, и количество реализаций должно быть равно отношению произведения 50 tцм к величине общего наименьшего кратное всех длительностей циклов.
Для моделирования графика можно применить как аналоговые, так и цифровые машины, однако аналоговая машина имеет в данном случае несомненные преимущества перед цифровой, особенно при наличии графиков индивидуальных электроприемников, снятых непосредственно на действующей промышленной установке. К числу основных преимуществ следует отнести: наглядность, возможность непосредственного ввода графика на пленке в читающее и вычислительное устройства, простота самого аналогового устройства и др.
Наиболее удобно записать индивидуальный график в виде теневого с помощью теневых регистраторов типа РТ, РТД или специально переделанного осциллографа. Эти приборы можно применять как при записи графика непосредственно в цехе, так и при записи расчетного графика. Поскольку расчетные графики обычно периодические, то достаточно записать только один период графика с учетом расчетной паузы. Для записи расчетного графика с помощью прибора типа РТ необходимо дополнительное устройство ручного ввода данных графика. Это устройство состоит из стабилизированного источника питания, потенциометра со шкалой выходных напряжений и реле времени.
На выходе потенциометра может быть включен как теневой регистратор с повышенной скоростью протягивания ленты, так и обычный. Записанные таким образом графики склеиваются в кольцо, длина которого выбирается так, чтобы она не была кратной длинам колец с другими графиками индивидуальных приемников.
1. Волобринский С. Д., Каялов Г. М., Клейн П. Н. и Мешель Б. С. Электрические нагрузки промышленных предприятий, «Энергия», 1964.
2. Каялов Г. М. и Куренный Э. Г., Основы расчета колебаний нагрузок в электрических сетей, «Электричество», 1967, № 2.
3. Куренный Э. Г., Основы теории и расчета пиковых нагрузок заводских электрических сетей, Канд. Диссертация, 1965.
4. Роткоп Л. Л., Статистические методы исследования на электронных моделях «Энергия», 1967.
5. Бусленко Н. П., Математическое моделирование производственных процессов на цифровых вычислительных машинах, «Наука», 1964.
6. Солодовников В. В., «Статистическая динамика линейных систем автоматического управления», Физматгиз, 1960.
7. Брусенцов Л. В., Бурок В. С., Долгих В. В., Вычислительное устройство для статистического анализа теневых графиков процессов. «Электромеханика», 1967, № 4.