
Источник информации: Пугачев B.C. Теория вероятностей и математическая статистика: Учеб. пособие.— 2-е изд., исправл. и дополи.— М.: ФИЗМАТЛИТ, 2002.- 496 с.
Непосредственное экспериментальное изучение сложных случайных явлений часто требует чрезмерно больших затрат средств и времени, а иногда и принципиально невозможно. Так, например, экспериментальное изучение функционирования сложной системы невозможно до тех пор, пока система не создана и не изготовлена. Между тем необходимо еще на стадии проектирования системы изучить все ее основные свойства, в частности, эффективность ее функционирования с учетом всех действующих на нее случайных возмущений. В таких случаях прибегают к статистическому моделированию изучаемых явлений. Статистическое моделирование в простейшей форме издавна применялось для решения различных задач. Современная вычислительная техника дает возможность имитировать практически без ограничений сложнейшие явления и процессы. Это привело к созданию и развитию метода статистического моделирования как научного метода исследования, позволяющего сочетать теоретические расчеты с имитацией различных экспериментов, а частично и с натурными экспериментами над отдельными элементами исследуемых систем.
Метод статистического моделирования основан на моделировании (имитации) изучаемого явления на ЭВМ с помощью теоретических зависимостей с непосредственным моделированием влияющих на его течение простейших (первичных) случайных факторов и на статистической обработке получаемых результатов.
Метод статистического моделирования оказался плодотворным и для решения ряда математических задач, не связанных с теорией вероятностей, например для вычисления интегралов, особенно многократных, решения некоторых уравнений и т.п. Применение этого метода к подобным задачам основано на моделировании такого случайного явления, вероятностными характеристиками которого служат искомые величины.
Основой метода статистического моделирования является моделирование случайных величин с заданными распределениями и событий с заданными вероятностями.
Рассмотрим сначала способы моделирования скалярных случайных величин. На основе результатов для моделирования случайной величины X с любой непрерывной функцией распределения F(x) достаточно уметь моделировать случайную величину Y, равномерно распределенную на интервале [0,1]. Получив реализацию y величины Y, найдем соответствующую реализацию х величины X по формуле х=F -1(y).
Для получения реализаций равномерно распределенных случайных величин применяются два принципа: физический и алгоритмический.
Физический принцип основан на использовании случайных физических явлений, например потоков частиц, испускаемых радиоактивными веществами, или собственных шумов электронных устройств. Действуя на соответствующие регистрирующие устройства, используемое физическое явление генерирует последовательность независимых случайных величин V1, V2,..., каждая из которых с вероятностью 0,5 принимает значение 0 или 1. Эту последовательность можно рассматривать как последовательность двоичных знаков числа, представляющего собой значение случайной величины
Можно доказать, что при неограниченной длине последовательности величина Y равномерно распределена на интервале [0,1] ( В действительности вследствие отсутствия строгой независимости величин V1, V2,... и из-за того, что вероятности значений 0 и 1 величин Vk не равны 1/2, распределение величины Y оказывается лишь приближенно равномерным ).
Действительно, случайная величина
имеет 2n возможных значений, и вероятность каждого из них равна 2-n. Функция распределения Yn определяется формулой
Представляя функцию распределения равномерного распределения на интервале [0,1] в виде F(y) = у и принимая во внимание, что 0 < [y2n]+1-y2n ≤ 1, получим 0 < Fn(y) - F(y) ≤ 2-n. Следовательно, Fn(y) → F(y) = у при n → ∞.
Реализации этой случайной величины Y вводятся в ЭВМ двоичными числами с тем числом знаков, с которым ЭВМ оперирует.
Для получения реализаций равномерно распределенной случайной величины алгоритмическим путем в ЭВМ вводят произвольное двоичное число, занимающее все разряды или часть разрядов какойлибо ячейки оперативной памяти. Над этим числом выполняют ряд простейших операций по специальной программе. Над полученным числом вновь повторяют те же операции и т.д. Генерируемая таким способом последовательность двоичных чисел, конечно, не будет случайной. Однако в достаточно длинном отрезке этой последовательности все числа с данным числом двоичных знаков будут встречаться практически одинаково часто. Поэтому взятое наугад число из этой последовательности можно считать реализацией случайной величины, равномерно распределенной на интервале [0,1]. Благодаря этому свойству таких последовательностей они называются последовательностями псевдослучайных чисел. Существуют много различных алгоритмов и программ формирования псевдослучайных чисел.
В отличие от последовательностей, генерируемых физическими источниками случайных явлений, одна и та же последовательность псевдослучайных чисел может неограниченно повторяться. Поэтому одну и ту же реализацию случайной величины можно использовать многократно. Это дает некоторые преимущества при решении ряда практических задач.
Нормально распределенную случайную величину на основании предельной теоремы можно моделировать как сумму независимых случайных величин, распределенных по любым законам. В частности, можно взять сумму независимых равномерно распределенных на интервале [0,1] случайных величин V1,... Vn. На основании предельной теоремы и результатов примера случайная величина

при достаточно большом n распределена приблизительно N(0,1). При этом случайная величина Z = mz + X√Dz будет распределена приблизительно N( mz,Dz).
Моделирование векторной случайной величины сводится к последовательному моделированию ее координат. При этом первая координата моделируется в соответствии с ее безусловным распределением, а каждая последующая координата — в соответствии с условным распределением при полученных ранее значениях всех предыдущих координат. Для моделирования случайного вектора X, распределенного нормально N( mx,Kx), можно воспользоваться любым каноническим разложением этого вектора:
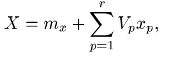
где r — ранг матрицы Kx. Выбрав координатные векторы так, чтобы дисперсии величины Vp были равны 1, сведем задачу к моделированию независимых случайных величин V1,... Vr, распределенных N(0,1).
Для моделирования события А с вероятностью р достаточно моделировать случайную величину Y, равномерно распределенную в интервале [0,1]. При попадании этой величины в интервал [0,р] считают, что событие А появилось, а при непопадании в интервал (р, 1] — что А не появилось.
Точно так же для моделирования полной группы несовместных событий A1,... Ar с вероятностями p1,... pr, p1+...+pr = 1,
достаточно моделировать величину Y, равномерно распределенную в
интервале [0,1], и считать, что появилось A1 при попадании Y в интервал [0,p1], появилось A2 при попадании Y в интервал [p1,p1 +p2]
и т.д., появилось Аr при попадании Y в интервал [p1+...+pr-1, 1].
Практические приложения метода
Применение метода статистического моделирования для решения вероятностных задач сводится к многократному непосредственному моделированию на ЭВМ изучаемого явления, включая моделирование тех случайных величин и событий, вероятностные характеристики которых известны, и последующему статистическому оцениванию вероятностных характеристик полученных результатов.
Так, например, при проектировании какой-либо сложной технической системы обычно многократно моделируют функционирование системы и действующие на нее возмущения (входные сигналы), вероятностные характеристики которых предполагаются известными. В результате моделирования получается ряд реализаций (выборка) всех величин, характеризующих работу системы (выходных сигналов). Статистическая обработка полученных данных дает оценки вероятностных характеристик величин, определяющих качество работы системы (как правило, ее точность). Выполнив моделирование для ряда вариантов и значений параметров системы, можно выбрать для дальнейшей разработки и реализации тот вариант, который наилучшим образом удовлетворяет поставленным требованиям.
Большим достоинством метода статистического моделирования является возможность включения в процесс моделирования некоторых реальных элементов системы, в том числе и не поддающихся математическому описанию, например человека или коллектива людей, участвующих в работе системы. Основным недостатком метода статистического моделирования является необходимость многократного моделирования случайного явления, чтобы получить выборку, по которой необходимые статистические характеристики могут быть оценены с достаточной точностью (представительную выборку).
Чтобы дать представление о зависимости точности метода статистического моделирования от числа опытов, воспользуемся результатами, где было показано, что точность оценок

математического ожидания и дисперсии нормально распределенной величины Y характеризуется средними квадратическими отклонениями
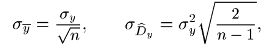
где σy — среднее квадратическое отклонение величины Y. В приведенной таблице показана зависимость относительной точности оценок математического ожидания и дисперсии от числа опытов n.

Из этой таблицы видно, что математическое ожидание можно оценить со средней квадратической погрешностью 16-19%, а дисперсию — со средней квадратической погрешностью 23-27 % при n — 30-40. Практически рекомендуется выбирать n ≥ 100, что обеспечит оценивание математического ожидания и дисперсии со средними квадратическими погрешностями 10% и 15% соответственно.
Простейшей вероятностной задачей, которую можно решить с помощью статистического моделирования, является задача вычисления вероятности попадания векторной случайной величины, особенно многомерной, в данную область В. Непосредственное вычисление интеграла, как правило, невозможно, а приближенное вычисление путем численного интегрирования требует большого объема вычислений. Моделируя случайную величину X с заданной плотностью f(x), можно за оценку вероятности Р(Х ∈ В) принять частоту попадания X в область В. Необходимый для расчетов объем вычислений будет, как правило, меньше, чем при численном интегрировании.
Точно так же можно оценивать моменты различных функций случайной величины X как выборочные средние соответствующих функций, полученные в результате статистического моделирования величины X.
интегралов. Чтобы показать применение метода статистического моделирования для решения математических задач, не имеющих вероятностного содержания, рассмотрим задачу вычисления интеграла
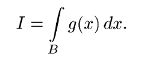
Если область В ограничена, то ее можно заключить в некоторый прямоугольный параллелепипед R со сторонами, параллельными осям координат. Представим интеграл I в виде
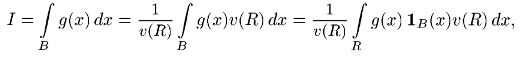
где v(R) — объем параллелепипеда R, а 1B(x) — индикатор области В, т.е. функция, равная 1 при Х ∈ В и 0 при Р(Х ∉ В). Последний интеграл можно рассматривать как математическое ожидание функции φ(Х) = g(X) 1B(X)v(R) случайной величины X, равномерно распределенной в параллелепипеде R. Моделируя эту случайную величину X, можно получить оценку интеграла I как выборочное среднее случайной величины φ(Х) = g(X) 1B(X)v(R):

При произвольной области В можно взять произвольную плотность f(x), не обращающуюся в нуль нигде в В, например невырожденную нормальную, и представить интеграл I в виде
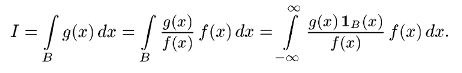
Последний интеграл можно рассматривать как математическое ожидание функции φ(Х) = g(X) 1B(X)/f(X) случайной величины X с плотностью f(x). Моделируя эту случайную величину X, можно получить оценку интеграла I как выборочное среднее величины φ(Х) = g(X) 1B(X)/f(X):
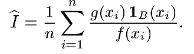
Чтобы дать представление о преимуществах метода статистического моделирования перед методами численного интегрирования, предположим, что для вычисления r-кратного интеграла I методами численного интегрирования требуется взять в области В mr узлов и что для расчета одного значения подынтегральной функции g(х) необходимо sr операций. Тогда для вычисления I методами численного интегрирования потребуется srmr операций. При применении метода статистического моделирования для вычисления I необходимо srn операций, где n — число опытов. Следовательно, относительный выигрыш машинного времени при применении метода статистического моделирования характеризуется отношением mr/n. Если считать минимальным необходимым числом узлов по каждой координатной оси m = 5, то при n = 100 метод статистического моделирования даст существенную экономию машинного времени уже при r = 4 ÷ 5. При увеличении кратности интеграла r преимущество метода статистического моделирования растет как показательная функция.