
Синтез дискретних пристроїв керування неперервними системами виконують одним з наступних шляхів:
• на основі неперервного об‘єкта регулювання синтезують неперервні пристрої керування, а потім перетворюють їх у дискретну форму (метод неперервних моделей);
• будують дискретні моделі об‘єкта регулювання і на їх основі синтезують дискретні пристрої керування.
Отже, в обох випадках треба вміти знаходити дискретні апроксимації аналогових передавальних функцій. Поставлену задачу можна виконати такими засобами:
- за допомогою Z-перетворення;
- заміною оператора аналогового інтегрування 1/s одним з операторів цифрового інтегрування;
- заміною нулів та полюсів на s-площині відповідними нулями та полюсами на Z-площині.
Отже, припустимо, що ми маємо неперервну динамічну систему з вхідним сигналом u(t) і вихідним сигналом y(t), що описується в області змінної Лапласа передавальною функцією (ПФ)
В цій ПФ характеристичний поліном (ХП) Gn(s) є нормованим за коефіцієнтом при старшому ступіні оператора Лапласа.
Використовуючи розкладення поліномів у чисельнику та знаменнику передавальної функції (1.1) на множники, отримуємо
де
Z=[z1 z2 ....zm] - вектор нулів;
P=[p1 p2 ....pn] - вектор полюсів;
K=Bm.
У просторі стану такий об‘єкт описується матричними рівняннями
x'(t) = Ax(t)+Bu(t), (1.3)
y(t) = Cx(t)+Du(t), (1.4)
де
x = [x1 x2 ....xn]T - вектор змінних стану;
A – матриця стану розміром n*n;
B – матриця входу розміром n*1;
C – матриця виходу розміром 1*n;
D – коефіцієнт прямого зв‘язку входу з виходом.
Задача полягає у визначенні при заданому періоді квантування еквівалентної дискретної передавальної функції (ДПФ)
або еквівалентних різницевих рівнянь
x[k+1] = Adx[k]+Bdu[k], (1.6)
y[k] = Cdx[k]+Ddu[k], (1.7)
тобто у побудові дискретної моделі неперервного об‘єкту. Під еквівалентністю в даному випадку розуміють збіг реакцій неперервної системи та її дискретної моделі на будь-яку вхідну дію. Найчастіше під збіжністю реакцій розуміють, що y[k] = y(tk) при u[k] = u(tk) , де tk = kT , k – номер кроку квантування.
Зв‘язок між рівняннями у просторі стану та передавальними функціями визначається виразами:
де
I – одинична діагональна матриця розміром n*n;
Adj(X) – союзна матриця (матриця, складена із алгебраїчних доповнень матриці-аргументу);
det(X) – визначник матриці.
В загальному випадку поставлена задача не має точного розв‘язку. Це пов‘язано з тим, що при дискретизації вхідного сигналу втрачається інформація про його значення між вузлами квантування. Отже, вихід дискретної моделі від цих значень залежати не може, у той час як реакція неперервної системи залежить від усіх значень вхідного сигналу.
Але все ж таки існують ситуації, у яких дискретна модель може бути точною у розумінні, викладеному вище. Для цього необхідно, щоб значення процесу u(t) при t k - 1 ≤ t < t k однозначно визначались послідовністю [u(t0), u(t1), ...u(tk-1),] . Таке має місце для імпульсних систем з амплітудно-імпульсною модуляцією першого роду та для цифрових систем керування, якщо вхідний процес, формується за допомогою ЕОМ.
В останньому випадку дискретний вхідний процес перетворюється у неперервний за допомогою екстраполятора [8, 9].
Найчастіше використовують екстраполятор нульового порядку (ZOH – Zero Order Hold), що перетворює решітчасту функцію часу у ступінчасту, тобто
u(t) = u(tk) при t k - 1 ≤ t < t k (1.10)
і має передавальну функцію
(1.11)
В класичній теорії керування відомий розв‘язок задачі дискретизації неперервного об‘єкту з екстраполятором нульового порядку на вході за допомогою Z-перетворення, яке називають ступінчато-інваріантним [1-3]:
(1.12)
Відповідне рішення у просторі стану має вигляд [4]:
Ad = eAT, Bd = A-1(Ad-I)B Cd = C, Dd = D. (1.13)
Для визначення дискретних передавальних функцій (ДПФ) за допомогою Z-перетворення для досить простих неперервних систем можна користуватися таблицями Z-перетворень [1, 5-7], а для більш складних – треба спочатку розкласти ПФ на суму простих дробів. Якщо
(1.14)
то невідомі коефіцієнти визначають за формулами
(1.15)
(1.16)
Для розрахунків на ЕОМ слід вважати більш перспективним напрямом використання формул (1.13), (1.9). Саме так виконується Z-перетворення в поширенні Control Toolbox пакета MATLAB (функція c2d) [4, 10-11].
При застосуванні замість ZOH екстраполятора першого порядку (FOH – First Order Hold), який утворює кусочно-лінійну апроксимацію дискретного сигналу
після Z-перетворення
отримують дискретну систему, у якої значення сигналів у перехідних процесах дорівнюють полусумі значень відповідних аналогових сигналів на кінцях періоду квантування:
(1.17)
Для підтвердження основних теоретичних положень розглянемо приклад, в якому неперервний об‘єкт має передавальну функцію
(1.18)
з трьома полюсами
p = [-0.1075+0.4417i, -0.1075-0.4417i, -0.2016], |p| = [0.4546, 0.4546, 0.2016]
та двома нулями
z = [0, -0.5].
Дискретні передавальні функції, отримані з ПФ (1.18) методом розглянутих Z-перетворень при T=2, мають вигляд:
(1.19)
(1.20)
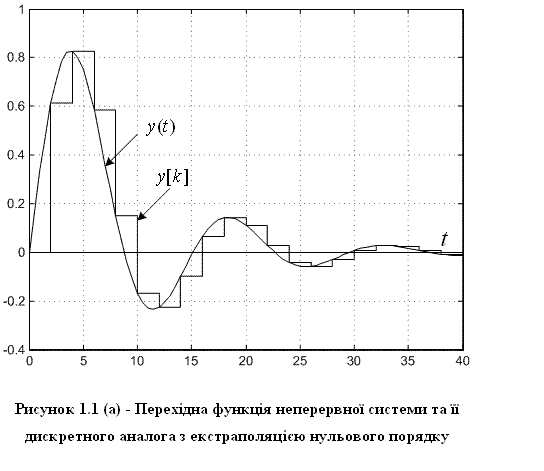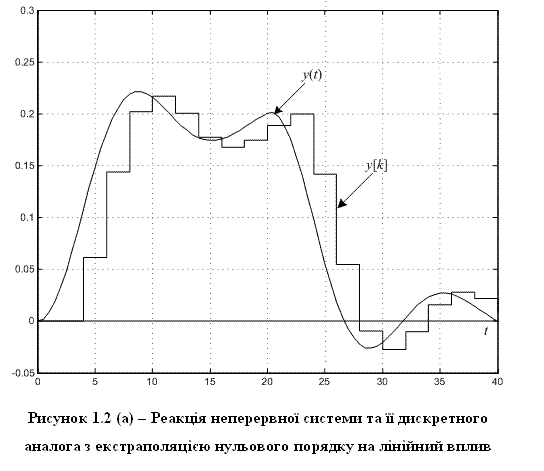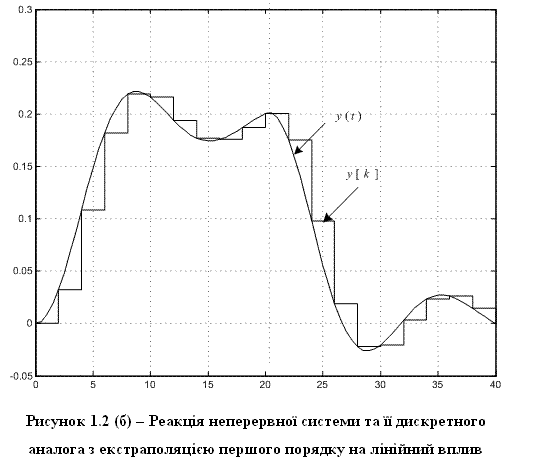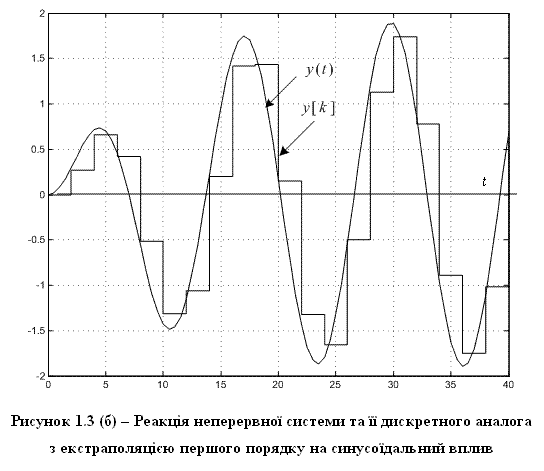
Перехідні функції вихідної неперервної системи з ПФ (1.18) ha(t) та дискретних систем з ДПФ (1.19) hz(t) і (1.20) hF(t) зображені на рис. 1.1. На цьому рисунку та далі частоту дискретизації (1/T=0.5) для наочності обрано близькою до частот полюсів неперервної системи, що взагалі не рекомендується.
Всі передавальні функції та їхні характеристики знайдено програмно в середовищі пакета MATLAB за методикою, яку буде викладено пізніше.
На рис. 1.2 показано реакції неперервної системи та її дискретних моделей на сигнал, що лінійно зростає від 0 до 1, а потім фіксується на досягнутому рівні:
u(t) = t/20 при t < 20; 1 при t ≥ 20. (1.21)
На рис. 1.3 показано реакцію систем, що розглядаються, на синусоїдальний вплив. Оскільки синусоїдальний вхідний сигнал між вузлами квантування набагато ближче до сигналу, який описується степеневим поліномом першого порядку, ніж до сигналу, що описується степеневим поліномом нульового порядку, то природно, що похибка дискретизації при використанні дискретної моделі з екстраполяцією першого порядку значно менше, чим при використанні дискретної моделі з екстраполяцією нульового порядку.
Отже, з аналізу наведених графіків видно, що варіант Z-перетворення треба обирати в залежності від вигляду вхідного сигналу, який прикладається до неперервного об‘єкта, що підлягає дискретизації.
Приблизні перетворення в більшій або меншій мірі наближаються до розглянутих Z-перетворень, але розраховуються значно простіше. Ще одною перевагою використання приблизних методів дискретизації неперервних динамічних об‘єктів є те, що, на відміну від точних Z-перетворень, загальна ДПФ послідовно з‘єднаних неперервних об‘єктів дорівнює добутку дискретних передавальних функцій, знайдених для кожної з неперервних ПФ окремо.
При приблизному визначенні дискретних передавальних функцій (ДПФ) цим методом можна використовувати такі підстановки:
s = (z-1) / T (2.1)
s = (z-1) / Tz (2.2)
s = 2(z-1) / T(z+1) (2.3)
Формули (2.1)-(2.3) пов‘язані з різними алгоритмами чисельного інтегрування, а саме: Forward Euler, Backward Euler та Trapezoidal. Підстановку (2.1) називають методом Ейлера, підстановку (2.2) – модифікованим методом Ейлера , а підстановку (2.3) – білінійним перетворенням або методом Тастіна (Tustin) [10].
Для демонстрації підстановочних методів дискретизації на рис. 2.1 показані перехідні функції неперервної інтегрувальної ланки W(s) = 1/s (верхній рядок), неперервної аперіодичної ланки з ПФ W(s) = 1/(4s+1) (нижній рядок) та їхніх дискретних апроксимацій, знайдених методами підстановок.
При дискретизації аперіодичної ланки отримують такі ДПФ:
Для порівняння наведемо ДПФ цієї ж ланки, отримані методом Z-перетворень:
Щодо використання цього методу у більшості джерел існує посилання тільки на те, як треба розрахувати дискретні полюси та сформувати характеристичний поліном ДПФ (1.5). Методику визначення нулів та коефіцієнта Kd передавальної функції (1.5) нам у літературі знайти не вдалося. Отже, прийшлося розробити її самим з використанням відомих положень теорії керування.
Згідно з цією методикою дискретизацію неперервного динамічного об‘єкту треба виконувати у такій послідовності:
1) знайти полюси pi ( i = 1, 2,....,n ) неперервної системи розв‘язанням характеристичного рівняння
Gn(s) = sn + αn-1sn-1 +....+ α1s + α0 = 0 (2.4)
або через пошук власних чисел матриці стану
P = eig(sI - A); (2.5)
2) знайти нулі zi ( i = 1, 2,...,m ) неперервної системи розв‘язанням рівняння
Hm(s) = βmsm + βm-1sm-1 +....+ β1s + β0 = 0 (2.6)
3) розраховувати відповідні дискретні полюси та дискретні системні нулі, тобто
pdi = exp(Tpi), i = 1, 2,....,n , (2.7)
zdsi = exp(Tzi), i = 1, 2,....,m ; (2.8)
4) якщо m < n - 1, доповнити ДПФ нулями квантування
zdkj = -1, j = m + 1, m + 2, ....., n-1; (2.9)
5) виділити із векторів аналогових нулів або полюсів нейтральні (тобто ті, що для неперервної системи дорівнюють 0, а для дискретної – 1) та підрахувати їх кількість ( μ та ν відповідно):
6) розрахувати коефіцієнт передачі в усталеному режимі неперервної системи за формулою
(2.10)
де K = βm ,
m1 = m - μ , n1 = n - ν - кількість ненульових аналогових нулів та полюсів відповідно;
7) розрахувати коефіцієнт Kd дискретного об‘єкта (див. ДПФ (1.5)) за формулою
(2.11)
де pd1i , zd1j неодиничні дискретні нулі та полюси відповідно.
ДПФ, отримана при дискретизації неперервного об‘єкту з ПФ (1.18) за викладеною вище методикою має вигляд:
(2.12)
Аналіз ДПФ Wm0 (z) (2.12) показує, що її полюси співпадають з полюсами, ДПФ Wz (z) (1.19) і WF (z) (1.20), отриманими методами Z-перетворень, а відповідні системні нулі незначно відрізняються один від одного. Крім того, ДПФ Wm0 (z) відрізняється від WF (z) кількістю нулів дискретизації. Отже, виникає ідея доповнити передавальну функцію (2.12) ще одним нулем дискретизації, для того, щоб наблизити її до ДПФ (1.20). При цьому в методиці дискретизації зміниться тільки пункт 4, який матиме такий вигляд:
4) якщо m < n , доповнити ДПФ нулями квантування
zdkj = -1, j = m + 1, m + 2, ..., n. (2.13)
Наведемо дискретну апроксимацію ПФ (1.18), знайдену за такою методикою:
(2.14)