Источник: Електромеханічні системи, методи моделювання та оптимізації. Збірник наукових праць VII Всеукраїнської науково-технічної конференції молодих учених і спеціалістів у місті Кременчук 2-4 квітня 2009 р - Кременчук, КДПУ, 2009 - 414 с.
Статичне моделювання (імітація) процесів х(t) у системах електропостачання дозволяє розв’язати нелінійні задачі, які не мають аналітичного розв’язку: наприклад, визначення параметрів ЕМС [1,2], оцінювання температур перевищення. Це потребує високої точності відтворення характеристик процесів. В практиці звичайно відомими є тільки функція розподілу й кореляційна функція (КФ), тому точність імітації оцінюється саме по цих характеристиках.
Оцінювання функції розподілу можна виконати за критеріями згоди (Колмогорова, К. Пірсона, Мізеса-Смірнова та ін.), але вони дають різні й навіть протилежні результати. Крім того, вони прямо не зв’язані з довірчими інтервалами для числових характеристик. Далі на основі загальних методів математичної статистики [3] приймається єдиний підхід до оцінювання якості імітації – шляхом визначення довірчих областей і обґрунтовується вибір значущості Ез. Довірчі інтервали для всіх числових характеристик вважаються симетричними відносно теоретичних значень.
Якщо спільно розглядаються n числових характеристик, то при заданому рівні значущості Eз межі довірчих інтервалів визначаються по вірогідності Eз n= 1 - Eз/n і ступеню свободи k=N-1, де N – кількість дослідів. По них з табл. 3 і 4 [3] знаходяться значення βсn і εαn, що дає:
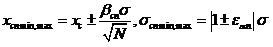
Межі довірчого інтервалу для коефіціента корреляції при N≥25 становлять [3]:
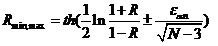
Якщо функція розподілу має один параметр (n=1), то для довірчої області потрібно накреслити дві межові функції. Наприклад, показників розподіл визначається лише хс, тому ці функції мають параметри хc min і хc max. Нормальний і рівномірний розподіли мають два параметри (n=2): хс і σ. Тут довірчі області визначаються зовнішніми межами чотирьох функцій розподілу з параметрами хc2min, σc2min, хc2min, σ2max, хc2max, σc2min і хc2max, σc2max. Якість імітації є прийнятною, коли статична функція знаходиться всередині довірчої області.
Довірча область для КФ також визначається з врахуванням меж двох параметрів: дисперсії σ2 і коефіцієнта кореляції. При τ=0 згідно з (2) Rmin = Rmax = 1, тому граничний діапазон по ординаті є обмеженим величинами σ2min і σ2max. При τ>0 межі становлять σ2maxRmin і σ2maxRmax. Теоретична КФ не повинна виходити за межі області.
Метод довірчих областей було застосовано до перевірки можливості імітації нормального випадкового процесу з експоненціальною КФ шляхом пропускання білого шуму через інерційну ланку. Реальний білий шум ξ(t) отримувався від генератора випадкових чисел, які дають послідовність ординат з малим кроком Δ. Обов’язовую умовою є некорельованість ординат на будь-якій відстані між ними. Це означає, що теоретична КФ К(τ) має вигляд трикутника з основою. Оскільки при τ≥Δ КФ дорівнює нулю, то перший доданок у (2) також дорівнює нулю, а тому межі довірчого інтервалу не залежать від τ.
В практиці звичайно Eз=0,5. Імітувалося N=1000 ординат. По Eз і k=999 з табл.4[3] було знайдено εα=0,047. При τ=0 межі довірчого інтервалу для дисперсій становили: σ22min=(0,9536σ)2=0,908σ2, σ22max=(1,047σ)2=1,096σ2. При τ≥Δ Rmax,max=±0,0015, а тому Кξmin,max(τ)=±0,0015•1,096=±0,00164. Отримані КФ далеко не завжди знаходяться у межах області, що свідчить про необхідність відбраковування таких процесів. Тому, не зважаючи на те, що функція розподілу реального білого шуму й вихідного процесу відтворювалися добре, довелося зробити висновок про необхідність використання іншого методу імітації.
Оцінювання статичних розподілів і кореляційних функцій доцільно виконувати методом довірчих областей.