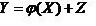
Источник: Пугачев B.C. Теория вероятностей и математическая статистика: Учеб. пособие.— 2-е изд., исправл. и дополн.— М.: ФИЗМАТЛИТ, 2002.- 351-354 с.
Для применения математических методов необходимо прежде всего установить соотношения между величинами, характеризующими рассматриваемые явления. Каждое такое соотношение представляет собой математическую модель данного явления. Так, например, закон Ньютона в механике и вся построенная на них классическая механика представляют собой совокупность моделей механических явлений. Уравнения Максвелла в физике представляют собой математическую модель электродинамических явлений.
В теории управления изучаются различные системы, поведение которых описывается некоторой совокупностью величин, причем одни величины носят характер внешних воздействий на систему и называются ее входными сигналами, а другие характеризуют работу системы, определяют ее воздействие на другие системы и называются ее выходными сигналами. Зависимость выходных сигналов системы от ее входных сигналов, используемая для изучения системы и ее взаимодействия с другими системами, представляют собой математическую модель этой системы.
Во многих случаях математическую модель можно построить чисто математическим путем на основе известных законов механики, физики и других дисциплин, пользующихся количественными соотношениями. Так, например, различные модели управляемого летательного аппарата можно построить математически, пользуясь законами механики.
Однако существуют и такие системы, для которых принципиально невозможно построить модели чисто математическим путем. Примером таких систем может служить человек или коллектив людей, выполняющий определенные функции, завод, отрасль промышленности, экономика и т.п. Современный научно-технический прогресс и все расширяющееся применение математических методов требуют создания математических моделей и для таких систем. Они необходимы, в частности, для решения современных задач управления.
Для построения моделей сложных систем приходится прибегать к экспериментальному исследованию самих систем или входящих в них подсистем и строить соответствующие модели путем статистической обработки полученных данных.
Модели, полученные на основе статистической обработки результатов экспериментального исследования функционирования систем, будем называть статистическими моделями. Методы построения статистических моделей составляют важный раздел современной математической статистики.
Построение статистической модели реальной системы или процесса часто называется идентификацией этой системы или процесса. Следует заметить, что это название не точно отражает существо данной задачи, так как никакая модель не может быть тождественна соответствующему реальному явлению.
Из сказанного следует, что задача построения модели явления, процесса или системы состоит в нахождении соотношений между величинами, описывающими течение данного явления, процесса или функционирования данной системы. Если эти соотношения позволяют по данным значениям одних величин однозначно определить значения других, то описываемая ими модель называется детерминированной. Если же эти соотношения по данным значениям одних величин определяют другие как случайные величины, то описываемая ими модель называется стохастической.
Как теоретические модели, выводимые математически из первичных законов, так и статистические модели, получаемые на основе статистической обработки результатов наблюдений, могут быть детерминированными или стохастическими. Так, например, зависимость Y=φ(x) , устанавливаемая по результатам по наблюдениям случайных величин Y и Х методом наименьших квадратов, представляют собой детерминированную модель. Если же учесть наблюдаемые в результате опытов случайные отклонения экспериментальных точек от кривой y=φ(x) и написать зависимость Y от Х в виде:
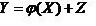
где Z – некоторая случайная величина, то получится стохастическая модель. При этом величины Y и Х могут быть как скалярными, так и векторными. Функция φ(x) может быть как линейной комбинацией данных функций, так и данной нелинейной функцией, параметры которой определяются методом наименьших квадратов. Число и вид функций в линейной комбинации, а также вид нелинейной функции φ(x) и число определяющих ее параметров могут быть любыми.
Приведенный простой пример показывает, что одному и тому же явлению могут соответствовать различные модели. Проблема построения модели системы включает и выбор подходящей формы этой модели, а также разумной степени ее сложности, совместимых с имеющимися экспериментальными данными.
Математические модели являются мощным инструментом познания реального мира. Они применяются для различных расчетов, проектирования систем, управления процессами и системами, прогнозирования разных явлений и т.д. Математические модели дают возможность открывать и предсказывать новые научные факты и закономерности.
Применение математических моделей в основном сводится к определению значений некоторых величин по известным значениям других величин. Значения последних могут быть или получены в результате наблюдений, или задаваться из каких - либо соображений.
Современное состояние и развитие вычислительной техники и связи дают возможность автоматизировать некоторые виды умственной деятельности человека, т.е приступить к решению проблемы создания искусственного интеллекта. Это особенно важно для разработка автоматических устройств – роботов – для выполнения работ в таких условиях, в которых человек не может существовать.
Все расширяющееся проникновение математических методов в сферу управления ставит задачу создания моделей и для процессов принятия решений. Перейдем к изучению методов построения статистических моделей. При этом мы ограничимся только такими моделями, которые описываются соотношениями между конечномерными векторами. К таким моделям относятся все дискретные системы, входные и выходные сигналы которых действуют только в определенные дискретные моменты времени. Для построения более сложных статистических моделей, в частности моделей, входные и выходные сигналы которых представляют собой функции непрерывно изменяющихся аргументов, необходимо применение теории случайных функций и раздела теории непрерывных стохастических систем.