
Дмитрієва О. М., Купирьова В.І.
Наукові праці Донецького національного технічного університету. Серія: «Електротехніка і енергетика», випуск 8 (140): Донецьк: ДонНТУ, 2008. – С. 101-105
The problem of definition of laws of distribution of processes on an exit of dynamic model of EMC is considered. Depending on volume of the initial information it is recommended to use Johnson's laws, Pirson's laws or beta-and gamma-distributions. Results provide reliability of an estimation EMC.
Постановка задачі. Оцінювання електромагнітної сумісності (ЕМС) здійснюється в два етапи: спочатку визначається реакція y(f) об’єкта на заваду, а потім – показники ЕМС [1]. На першому етапі труднощів не виникає, бо реакція й завада зв’язані між собою лінійним диференціальним рівнянням. На другому ж етапі задача є нелінійною, оскільки для врахування потужності реакції потрібно підносити реакцію до квадрату.
Дія процесу z=y2(t) не може виявитися миттєво, тому потрібно враховувати інерційність об’єкта. Це реалізується пропусканням квадрата реакції або через інерційну ланку, або через вікно Дірихле. У першому випадку ланка має сталу часу T, яка співпадає зі сталою інерції об’єкта. На виході ланки протікає квадратичний інерційний процес (КІП) wT(f). Такий «інерційний» принцип прийнято при нормуванні дози флікера напруги [2, 3], де T = 0.3 s. У другому випадку виконується поточне осереднення процесу z(f) на заданому інтервалі. Такий підхід використано в [3] при нормуванні відхилень частоти та відхилень, несиметрії і несинусоїдальності напруги (ширина інтервалу – від 3 до 60 с).
Для короткості далі розглядаються лише КІП, але всі висновки розповсюджуються і на квадратичні кумулятивні процеси. Задача полягає в визначенні розрахункових максимумів wTmax і мінімумів wTmin КІП з інтегральними ймовірностями Ex and 1 - Ex(в [3] Ex = 0.05). Для цього потрібно визначити імовірнісні закони розподілу КІП.
Точний розв’язок задачі є відомим тільки для завад у вигляді періодичної послідовності прямокутних імпульсів, а також телеграфного сигналу [1]. У інших випадках можуть бути визначені лише моменти ймовірнісного розподілу [4, 5].
В практиці реакції звичайно являють собою стаціонарні випадкові процеси з нормальним розподілом ординат. Метою статті є розробка наближеніх методів оцінювання розрахункових екстремумів КІП саме для таких процесів.
Використання рядів. В [5] щільність розподілу рекомендується апроксимувати рядом Еджуорта – за формулою (34.15), використовуючи середнє значення wT,стандарт σwT, асиметрію SkT і ексцес EhT. З урахуванням співвідношень [6, 7]:
ФФn+1=(-1)nФФ'(x)Hn(x), ФФ'(x)=φФ(x), H0(x)=1,
Hn+1(x)=xHn(x)-nHn-1(x), n=0,1,...,
запишемо його у вигляді
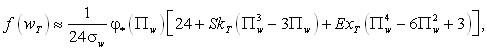 (1)
(1)
де Hn (x) - багаточлен Ерміта, Пw=(wT-wTn)/σw ФФ(x) and φФ(x) - функція і щільність стандартного нормального розподілу з нульовим середнім значенням й одиничним стандартом.
Проілюструємо використання цього ряду на прикладі, коли точний розв’язок є відомим: при T = 0коли КІП співпадає з z (f).Спочатку розглянемо випадок, коли середнє значення yc реакції дорівнює нулю, що є характерним для дози флікера й несинусоїдальності напруги. У цьому разі формула (2.39) з [1] дає щільність

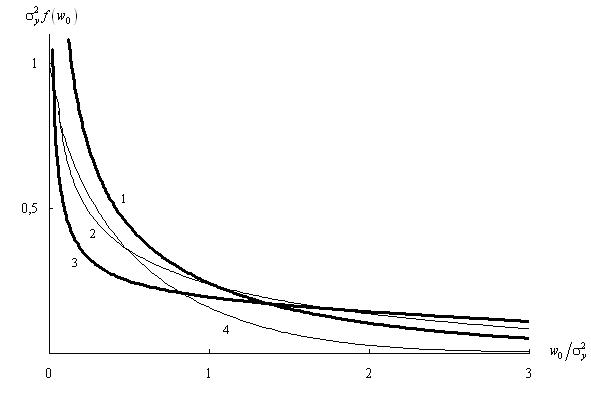
де w0 = z, σy -стандарт реакції. Графік щільності розподілу представлено на рис. 1 кривою 1, де вісі координат прийняті у відносних одиницях.

За загальними формулами теорії ймовірностей визначимо числові характеристики розподілу: wn=σy2, σno=√2σy2, Skno=2√2, Exno=12 а також другий mn2=3σy4 і третій mn3=8σy4 початкові моменти. Якщо взяти тільки перші дві характеристики, то у формулі (1) залишається перший доданок, а тому розподіл є нормальним (крива 2). Врахування ще й асиметрії або асиметрії й ексцесу дає щільності, графіки яких представлені кривими 3 і 4.
Розрахунки показують, що навіть при великих сталих часу криві щільностей мають досить великі області від’ємних абсцис і ординат (рис. 27 в [5]). Це суперечить фізичному смислу, тому ряд Еджуорта є неприйнятним.
Перейдемо до наближення щільності розподілу рядом Лагерра, у якому звичайно використовують три числові характеристики [6].
Позначимо
η=wn2/σwT2, λ=wn/σwT2
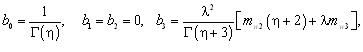
де Г(x) - гама-функція, x - аргумент.
Нульовий член узагальненого полінома Лагерра дорівнює одиниці, а третій становить
L3(x)=1/6[η(η+1)(η+2)-3x(η+1)(η+2)+3x2(η+2)-x3] where η>0
Шукана щільність розподілу має вигляд:
f(wT)≈ληwTη-1exp{-λwT}[b0+b3L3(λwT)]При b3 = 0 формула (4) дає гама-розподіл

з параметрами (3). Зокрема, для приклада, що розглядається, маємо η=0.5, λ=σy2, b0=1/√π, b3=0 тому формула (4) співпадає з (2) і (5), тобто у цьому випадку ряд Лагерра дає точний розв’язок (крива 1).
Зміну виду щільностей при зростанні сталої часу проілюструємо на прикладі реакцій з нульовим середнім значенням і експоненціальною кореляційною функцією, яка має параметр α. При T = 0 крива 1 (рис. 1 і 2) має нескінченну ординату і спадає монотонно, а при T> 0 Як і для гама-розподілу, можна вважати, що нормалізація практично відбувається при а при T > 0 криві щільності починаються з нуля й мають що найменше один максимум. Збільшення сталої часу зменшує діапазон змінення абсцис і збільшує перший максимум (криві 2 і 3). При When αТ = 10 the curve 3 крива 3 є майже симетричною, але вона ще відрізняється від кривої нормального розподілу, оскільки її максимум зсунуто ліворуч від середнього значення wn/σy2=1 Як і для гама-розподілу, можна вважати, що нормалізація практично відбувається при αТ ≥ 30 [8].

Щільності можуть мати від’ємні ординати, але вони є значно меншими в порівнянні з рядом Еджуорта. Наприклад, крива 2 на рис. 2 при абсцисі 4 має ординату –0,00083. За цієї обставини використання ряду Лагерра є більш коректним.
Для порівняння на рис. 2 приведені криві 4 і 5, які відносяться до гама-розподілу (при b3 = 0). Кожна з них має один максимум і тільки позитивні ординати.
Перейдемо до випадку, коли середнє реакції значення відрізняється від нуля (наприклад, несиметрія напруг). Тут точний розв’язок дається формулою:
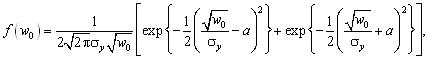
де a=yn/σy величина, яка є зворотною від коефіцієнта варіації.При ус=0 вирази (2) і (6) співпадають.
Крива 1 на рис.3 відноситься до a=0,а тому співпадає з кривими 1 на попередніх рисунках.Крива 3 розрахована за формулою(6) при а=± 1.Як видно, наявність ненульового середнього значення виду кривої щільності не змінює, але робить її згасання у зоні великих абсцис більш повільним, а малих абсцисах – навпаки.
Криві 4 і 2 представляють наближені розв’язки: ряд Лагерра (4) і гама-розподіл (5). Вони також по-різному розташовуються відносно кривої 1. Це призводить до суттєвого розходження у розрахункових максимумах, тому нехтувати величиною b3 в (4) недопустимо.
У всіх випадках середнє значення дорівнює квадрату ефективного значення реакції
wn=ya2=yn2+σy2 (7)
Для реакції з експоненціальною кореляційною функцією стандарт розраховується за аналогією з формулою (4.55) у [1]:
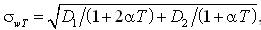
де D1=2σy4, D2=4yn2σy2 – доданки дисперсії квадрата реакції. За щільністю визначається функція розподілу F(wT) що дозволяє знайти розрахункові мінімум і максимум з рівнянь:
F(wTmin)=Ex,F(wTmax)=1-Ex(9)Використання щільності розподілу. Вибір закону розподілу КІП залежить від обсягу початкової інформації. Якщо відомими є чотири початкових моменти, то природно використовувати чотирипараметричні розподіли Пірсона або Джонсона [8]. Невідомі параметри розподілу, в тому числі й діапазон (wTm, wTM) можливих значень ординат, розраховуються по моментах числовими методами. У багатьох випадках можна прийняти wTm = 0, що дозволяє перейти до трипараметричних законів розподілу.
Якщо діапазон є відомим, то достатньо знати лише середнє значення wс і стандарт σwT. У цьому випадку доцільно використовувати бета-розподіл зі щільністю
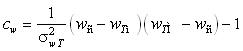
де γ and η – параметри, κ =wTM-wTm – ширина діапазону, В(γ,η) – бета-функція. При
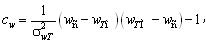
параметри

Труднощі у визначенні параметрів потребують розробки простих орієнтовних методів. При малих середніх значеннях (до 10 % від σу ) нами пропонується приймати гама-розподіл (5). Таку можливість зумовлено наступним. При T = 0, коли асиметрія і ексцес є найбільшими, цей розподіл дає точний розв’язок. Невелика похибка буде і при дуже великих сталих часу. У проміжних випадках у важливій для практики зоні розрахункових максимальних значень щільності (4) і (5) відрізняються мало. Гама-розподіл не дає незакономірних коливань і від’ємних ординат. Вирішальною ж позитивною якістю є те, що гама-розподіл потребує мінімального обсягу інформації: лише середнє значення і стандарт, які визначаються за середнім значенням і кореляційною функцією реакції.
При великих середніх значеннях ряд Лагерра доцільно використовувати тільки для розрахунку найбільшого можливого значення wTM ординат КІП. Для цього у друге рівняння (9) потрібно підставити межову ймовірність 0,001, яка в практиці вважається найменшою при визначенні розрахункового значення wTM > wTmax. Найменше можливе значення wTM приймається рівним нулю. Шукану щільність апроксимують бета-розподілом, параметри якого, окрім знайдених wTm і wTM, визначаються формулами (11). Розрахункові екстремуми отримуються розв’язком рівнянь (9).
Висновки.
Використання ряду Еджуорта для визначення щільності розподілу ординат квадратичних інерційних і кумулятивних процесів є некоректним.
Щільність розподілу доцільно апроксимувати розподілами Джонсона або Пірсона – при відомих чотирьох моментах розподілу, гама-розподілом – при перших двох моментах розподілу й малих середніх значеннях реакцій, бета-розподілом – при великих середніх значеннях, визначаючи найбільше можливе значення за рядом Лагерра з межовою ймовірністю 0,001.
Кузнецов В. Г., Куренный Э. Г., Лютый А. П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения. – Донецк: Норд-Пресс, 2005. – 250 с.
CEI/IEC 61000-4-15. Electromagnetic compatibility – Part 4, Section 15: Flickermeter – Functional and design specification. 1997.
ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Электромагнитная совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.
Васильев Д.В. Инерционное детектирование случайной последовательности прямоугольных импульсов. – Изв. вузов. Радиофизика, 1960. – С. 1011-1021.
Свешников А.А. Прикладные методы теории случайных функций. – М.: Наука, 1986. – 463 с.
Тихонов В.И., Статистическая радиотехника. – М.: Сов. радио, 1966. – 678 с.
Математический анализ: Функции, пределы, ряды, цепные дроби / Под общ. Ред. Л.А. Люстерника, А.Р. Ямпольского. – М.: Физматгиз, 1961. – 439 с.
Плескунин В.И., Воронина Д.Е. Теоретические основы организации и анализа выборочных данных в эксперименте. – Л.: изд-во Ленинградского ун-та, 1979. – 232 с.