 (6)
(6)Курінний Е.Г., Дмитрієва О. М., Ленко В.Г.
Наукові праці Донецького національного технічного університету.
The models of electromagnetic compatibility for estimation of influence of voltage on lamps are proposed. The peculiar properties of parametric identification of models are considered. The effectiveness of saving lamps using is shown.
Постановка задачі. В Україні на освітлення витрачається до 24 млрд. кВт*г за рік, а питомі витрати електроенергії у 1,5 рази вищі, ніж у розвинених країнах [1]. Це робить задачу енергозбереження в освітлювальних системах дуже актуальною. Вважається, що її вирішення затримується від того, що енергозберігальні лампи (ЛЕ) мають високу вартість. Однак при цьому не враховується, що внаслідок низької якості напруги в освітлювальних електричних мережах збитки від швидкого старіння ламп розжарювання (ЛР) і погіршення зору людини можуть привести до протилежного висновку. Для економічного обґрунтування доцільності переходу до ЛЕ потрібно оцінювати електромагнітну сумісність (ЕМС) ламп.
Метою статті є розробка моделей ЕМС, які дають об’єктивну оцінку впливу напруги на лампи. Всі параметри режиму вимірюються у системі відносних одиниць (в.о.), де базовою величиною є номінальна напруги, яка у цій системі дорівнює одиниці.
Вхідні процеси. У загальному випадку [2] будемо використовувати звідні нелінійні моделі, нелінійні частини яких відтворюють статичні характеристики, а лінійні – динамічні властивості ламп. На вхід моделі надходить процес U(t) змінення діючих значень напруги, який може бути періодичним з частотою змінення λ або випадковим, коли частота змінюється від нуля до нескінченності. Необмежений частотний діапазон буде і при розкладанні періодичних процесів у ряди Фур’є.
При проведенні експериментальних записів графіків U(t) виникає питання трактовки поняття «діючого значення». Для того, щоб одержати безперервний графік U(t), потрібно виконати квадратичне осереднення графіка u(t) миттєвих значень напруги на інтервалі θ:
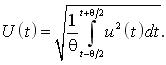 (1)
(1)
Згідно [3] інтервал осереднення дорівнює половині тривалості tf циклу синусоїди 50 Гц, тобто θ = 0,01 с. У цьому стандарті замість безперервного рекомендується дискретне осереднення з кроком 0,01 с. В результаті графік діючих значень являє собою гратчасту функцію, ординати якої співпадають з (1) при t = 0; 0,01; 0,02 с, … У стандарті не вказано спосіб з’єднання ординат цієї функції: з рис. А.1 витікає, що ординати повинні з’єднуватися прямими лініями, а на рис. Б.1 прийнято східчастий графік. На рис. В.2 показано обидва способи. Така невизначеність призводить до різних перехідних функцій, які ідентифікуються за одним і тим самим вихідним графіком (див. додаток). На наш погляд, потрібно виходити з (1).
Аналогічні труднощі виникають і при визначенні амплітудно-частотної функції (АЧФ), коли на вхід моделі потрібно подавати гармонічні сигнали різної частоти λ. В [4] для миттєвих значень напруги прийнято відому формулу
u(t)=sinωft(1+Bsinωλt) (2)
для амплітудної модуляції сигналу з несучою частотою 50 Гц і кутовою частотою модуляції ωλ = 2πλ при одиничному середньому значенні модульованої напруги. Вважається, що на вхід моделі подається процес
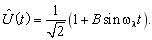 (3)
(3)
Насправді ж таке припущення є прийнятним лише при частотах модуляції, значно менших за несучу частоту. При великих частотах підстановка (2) в (1) дає результат, який відрізняється від (3). Враховуючи, що піднесення у квадрат подвоює частоту синусоїди, вираз (3) можна використовувати при частотах модуляції до 10-20 Гц.
Статичні моделі. Статичні характеристики ламп визначаються експериментально при незмінних значеннях параметрів режиму, коли будь-які способи визначення діючих значень дають єдиний результат. Розглянемо спочатку світловий потік, для якого звичайно використовується ступеневий вираз
Ф=Ua (4)
де a - показник ступеня.
Якщо напруга змінюється у невеликому діапазоні, виконується лінеаризація у точці з абсцисою Ux середини діапазону:
Ф≈Uxa+aUxa-1(U-Ux)=aUxa-1U+(1-a)Uxa
Експерименти звичайно виконуються в діапазоні напруг, який є симетричним відносно номінальної напруги, коли Ux = 1. У цьому випадку
Ф≈aU+1-a (5)
Відносна похибка лінеаризації у процентах становить
 (6)
(6)
В [4] вхідним вважається процесU2(t) тобто замість (4) використовується вираз
Ф=U2k (7)
з показником ступеню k. Для звідної нелінійної моделі при
k=a/2 (8)
формули (4) і (7) дають однаковий світловий потік.
Однак при лінеаризації результат буде різним. Справа в тому, що на вхід моделі надходить процес змінення діючих значень напруги, а не їх квадратів. Очевидно, що після лінеаризації процес має бути лінійною функцією U – як (5). Якщо ж в точці Ux = 1 здійснити лінеаризацію по квадратах напруги, то замість (5) отримаємо вираз
Ф≈kU2+1-k (9)
який є нелінійним відносно напруги.
Для ілюстрації на рис. 1 приведено результати експериментальних досліджень, де світлі кружки відносяться до газонаповненої лампи розжарювання типу E27CL потужністю 60 Вт, 230 В (фірма Philips, виробництво Іспанії), а темні – ЛЕ типу Ecoton E27, 20 Вт, 230 В (Philips, Голландія).

Статична характеристика ЛР з похибкою не більше 1,38 % апроксимується виразом (4) при а = 3,8 (крива 1). Для ЛР без газу показник ступеню дорівнює 3,6 [5, 6]. Якщо врахувати співвідношення (8), то отриманий результат практично співпадає з даними табл. 3 з [4], де вказано значення k = 1,87. У формулі ж (9) з [4] прийнято округлене значення 1,9, яке дає повний збіг. Виразу (5) відповідає пряма лінія 1'. Підставивши в (6) допустиму похибку –10 %, отримаємо допустимий діапазон лінеаризації: від 0,887 до 1,178. При похибці –5 %діапазон є вужчим: від 0,914 до 1,115.
Статичну характеристику ЛЕ доцільно апроксимувати лінійною залежністю. Для цього треба використовувати вираз (5), який забезпечує проходження прямої лінії через точку (1; 1). Можна показати, що за методом найменших квадратів параметр
 (10)
(10)
де N – кількість експериментальних точок (знак ~).
Для ЛЕ, що розглядається, формула (10) дає значення а = 0,7405. Відповідну характеристику
Ф=0,7405U+1-0,7405=0,7405U+0,2595 (11)
представлено на рис. 1 прямою 2. Найбільша похибка апроксимації становить усього 0,38 %. Наявність в (11) постійного члену свідчіть про те, що екстраполяція отриманої лінійної залежності за межі діапазону, у якому змінювалася напруга під час експерименту, не є коректною. Дійсно, при відсутності напруги світловий потік також є від’ємним, але формула (11) дає значення 0,2595 в.о.
В [4] отримано значення показників ступеню, які з перерахуванням згідно (8) становлять: а = 3,74 – для галогенної лампи HL20 потужністю 20 Вт; 1,24 – для люмінесцентної лампи FL36ind 36 Вт; 0,91 – для ЛЕ ESL11 11 Вт. В [6] для люмінесцентних ламп прийнято середнє значення 1,5.
Аналогічно вибираються моделі і для інших параметрів режиму. Наприклад, модель лампи ЕМС за струмом по суті є нелінійною. Дійсно, якби опір лампи не залежав від напруги, то у відносних одиницях було б І = U, тобто статична характеристика була б прямою з одиничним кутовим коефіцієнтом. Насправді ж при зменшенні (збільшенні) напруги, а також і температури волоска розжарювання, опір лампи зменшується (збільшується). Тому при U < 1 статична характеристика буде проходити над прямою, а при U > 1 – під нею. В точці (1; 1) характеристика має перегін. Такий же вигляд має і статична характеристика за потужністю (рис. 3-10 в [5]). Однак в діапазоні напруг від 0,85 до 1,15 в.о. статичні характеристики можна лінеаризувати. Для збереження виразу Р = UI лінеаризується одна з характеристик. Так, струм з похибкою, меншою ніж 0,9 %, можна розраховувати за формулою
I≈0,533U+0,467
Похибка виразу для потужності
P≈1,55U-0,55
не перевищує 2,7 %.
Динамічні моделі. На лінійну частину моделі надходить світловий потік, а процес ФL(t) на виході описується лінійним диференціальним рівнянням. Найпростішим є рівняння першого порядку
TπФL'(t)+ФL(t)=Ф(t)=Ua(t) (12)
яке враховує інерційність лампи – сталою часу Tπ.
У випадку лінеаризації нелінійної частини моделі згідно (5) процес на виході моделі буде мати дві складові: постійну ФL1(t) і змінну ФL2(t). Відповідна модель буде складатися з двох ланок: пропорційної з коефіцієнтом передачі 1 – а і ланки з передавальною функцією
Hπ(Ρ)=ФL2(Ρ)/U(Ρ)(13)
де Ρ – оператор. При використанні рівняння (12) маємо
Hπ(Ρ)=a/(TπΡ+1) (14)
Якщо ж виходити з (9), передавальна функція
Hπ'(Ρ)=ФL2(Ρ)/U2(Ρ)=H(Ρ)/2 (15)
буде вдвічі меншою за (13). Далі використовуються формули (5) і (8) – як такі, що відповідають смислу лінеаризації.
При параметричній ідентифікації моделей ЕМС потрібно враховувати поняття «діючого значення», яке було відмічено раніше. Теоретичного вирішення проблеми не існує. До проведення спеціальних досліджень, у першому наближенні будемо використовувати передавальну функцію (14), якій відповідає АЧФ
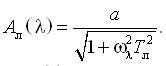 (16)
(16)
Проілюструємо такий підхід на прикладі результатів визначення АЧФ в [4], де опитні точки бралися до 35 Гц. Розглянемо АЧФ люмінесцентної лампи. На рис. 2 кружками показані опитні точки, а крива 1 отримана розрахунком за формулою (6) з [4]. Вона відноситься до лінійної системи, яка містить чотири послідовно з’єднані ланки: пропорційну з α = 1,24, дві форсуючі зі сталими часу 0,00571 с і –0,0057 с, а також інерційну зі сталою часу 0,01529 с. АЧФ має мінімум при частоті 24 Гц, а потім починає зростати до нескінченності, що суперечить фізичному смислу. Якщо врахувати опитні точки тільки до 20 Гц, то вираз (16) при α = 1,24 і Тл = 0,0085 с апроксимує їх з найбільшою похибкою 6,61 %, що цілком допустимо. Відповідна крива 2 при збільшенні частоти монотонно зменшується.

Модель ЛЕ потужністю 11 Вт в [4] прийнято у вигляді пропорційної ланки з коефіцієнтом α = 0,91 і коливальної ланки зі сталими часу 0,0029 і 0,00538 с. Відповідна АЧФ добре апроксимує опитні точки. Проте, якщо взяти точки до 20 Гц і прийняти вираз (16), то при Тл = 0,0037 с похибка апроксимації не перевищує 5,3 %.
Щодо ЛР і галогенної лампи, то модель у вигляді інерційної ланки прийнято і в [4], де отримано сталі часу 0,02066 і 0,049 с. Коли врахувати опитні точки лише до 20 Гц включно, сталі часу зміняться мало: 0,0217 і 0,0516 с.
Відхилення і коливання напруги. В [3] відхилення напруги визначаються через «усталене значення» напруги виду (1) при θ = 60 с. Цей інтервал осереднення згідно [6] приблизно моделює інерційність об’єкту зі сталою часу 26,7 с. Сталі часу ламп є значно меншими, тому застосування однохвилинних відхилень призводить до суттєвого заниження оцінок ЕМС. Більш того, оскільки у загальному випадку модель ЕМС є нелінійною, на її вхід не можна подавати відхилення напруги, а тільки саму напругу.
ЕМС потрібно оцінювати за процесом на виході моделі. Представлення лінійної частини у вигляді інерційної ланки значно спрощує викладки, а при можливості лінеаризації задача розв’язується аналітично (п. 2.5 в [7]).
Якщо в порівнянні зі сталою часу лампи напруга змінюється повільно, то оцінювання ЕМС виконується у рамках статичних моделей (п. 2.3 в [7]). Наприклад, у випадку гармонічних коливань з похибкою до 10 % це допустимо при частотах до 20,8 Гц для ЛЕ, до 9,1 для люмінесцентної лампи, до 1,5 Гц для галогенної лампи і 3,7 Гц для ЛР. Якщо допустиму похибку знизити до 5 %, то діапазони становляться вужчими: відповідно 14,1; 6,2; 1 і 2,5 Гц. Чим ближче коефіцієнт α до одиниці, тим менше змінення напруги впливають на лампи. Наприклад, відхилення напруги на –10 % зменшує світловий потік ЛР на 33 %, а енергозберігальної Ecoton E27 – усього на 7,5 %
Коливання напруги оцінюються за дозою флікеру Рst [3, 8]. У зважувальному фільтрі флікер-моделі прийнята ЛР 60 Вт. Для врахування фактичних ламп потрібно АЧФ Аф(λ) фільтру поділити на АЧФ лампи розжарювання і помножити на АЧФ лампи, що розглядається. За смислом доза флікеру є тим меншою, чим менше коефіцієнт α і чим більше стала часу лампи.
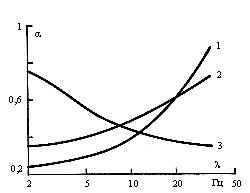
Проілюструємо зменшення доз на прикладі гармонічних коливань. У цьому випадку залежність дози флікеру від частоти є пропорційною АЧФ зважувального фільтру. Тому за рівними обставинами коефіцієнт α зменшення доз при зміненні ЛР на інші лампи визначається відношенням АЧФ ламп. На рис. 3 показано відповідні залежності: 1 – для ЛЕ 11 Вт, 2 – для люмінесцентної лампи 36 Вт, 3 – для галогенної лампи 20 Вт. Різний характер кривих пояснюється тим, що у ЛЕ і люмінесцентної ламп діють протилежні фактори: у них коефіцієнт α є меншим, ніж у ЛР, проте сталі часу менші. У галогенної лампи і менший коефіцієнт α і більша стала часу зменшують дозу. У частотній області до 5 Гц з точки зору зменшення дози флікеру використання ЛЕ є найбільш ефективним. У зоні частот вище 20 Гц починає виявлятися те, що у ЛЕ менша стала часу, ніж у люмінесцентної лампи, а тому крива 1 приходить вище кривої 2. При частотах 7-10 Гц найбільш ефективними виявляються галогенні лампи.
В [9] орієнтовні оцінки зменшення доз запропоновано здійснювати по відношеннях коефіцієнтів α. Розрахунки показують, що з похибкою до 10 % це можливо робити до частот: 2,61 Гц – для ЛЕ; 2,84 Гц – для люмінесцентної лампи і 4,6 Гц – для галогенної лампи
Висновки. 1. Для визначеності процес змінення діючих значень напруги доцільно отримувати безперервним квадратичним осередненням миттєвих значень на інтервалі 0,01 с.
2. Використання однохвилинних відхилень напруги занижує оцінки ЕМС ламп. Вплив напруги на лампи потрібно оцінювати за процесами на виході моделей ламп, а при повільних зміненнях напруги – у рамках статичних моделей.
. Для суттєвого покращення ЕМС доцільно застосовувати енергозберігальні лампи замість ламп розжарювання, які найбільш чутливі до змінення напруги і дають найбільшу дозу флікеру при коливаннях напруги в електричній мережі.
Додаток. Одним з способів ідентифікації моделі лампи є подання на лампу стрибка напруги величиною В від початкового значення U0 до U0 + В. Це можна зробити в момент переходу синусоїди через нуль. Тоді на ділянці часу від t = –tf / 2 до нуля буде синусоїда з амплітудою √ 2U0, а від нуля до tf / 2 – з амплітудою √ 2(U0+B)
Для поточного значення часу інтервал осереднення захоплює першу синусоїду від –tf / 2 + t до нуля і другу синусоїду від нуля до t. Згідно (1) при 0 ≤ t ≤ tf / 2 отримаємо
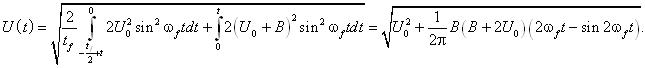
Розрахунки за цим виразом дають криву 1 на рис. Д.1, де прийнято U0 = 1 і В = 0,1.

Якщо ж виконувати дискретне квадратичне осереднення, то до t ≤ 0 ординати гратчастої функції будуть дорівнювати U0, а після t ≥ tf / 2 вони стануть рівними U0 + В. Межові ординати (кружки на рис. Д.1) можна з’єднати прямою лінією 2 або східцем 3. Очевидно, що рішення диференційного рівняння (12) будуть різними, а тому результати ідентифікації не будуть співпадати
Для розв’язання цієї невизначеності в експерименті потрібно записувати миттєві значення напруги і світлового потоку, а потім виконувати їх квадратичне осереднення згідно (1). Знаючи процес U(t), для моделі лампи, що обирається, записують теоретичне рішення для реакції на цей процес. В рішенні параметри моделі є невідомими. Їх визначають за методом найменших квадратів, використовуючи записаний процес Φ˜L(t)
Наприклад, якщо гіпотетична модель має передавальну функцію (14), то загальне рішення рівняння (12) має вигляд
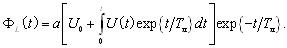
Стала часу лампи визначається з рівняння

рішення якого залежить від виду процесу U(t).
До цього вважалося, що інерційність фотоелемента є дуже малою. Якщо таке припущення не є коректним, то спочатку або виконують корекцію записаного процесу Φ˜L(t) згідно [10], або теоретичне рішення знаходять для моделі, яка складається з послідовно з’єднаних моделей лампи і фотоелемента.
ЛІТЕРАТУРАПилипчук Р.В., Щиренко В.В., Яремчук Р.Ю. Промышленное освещение. Методико-справочное пособие – Тернополь, 2006. – 432 с.
Свешников А.А. Прикладные методы теории случайных функций. – М.: Наука, 1986. – 463 с.
ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Электромагнитная совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.
Brauner G., Hennerbichler C. Lamp models for flicker simulation and illumination planning. – Fifth International Conference: Electrical Power Quality and Utilisation. – Cracow, 1999. – Р. 235-240.
Епанешников М.М. Электрическое освещение. – М.: Энергия, 1973. – 352 с.
Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. – Киев: Наукова думка, 1984. – 271 с.
Кузнецов В. Г., Куренный Э. Г., Лютый А. П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения. – Донецк: Норд-Пресс, 2005. – 250 с.
CEI/IEC 61000-4-15. Electromagnetic compatibility – Part 4, Section 15: Flickermeter – Functional and design specification. 1997.
Куренный Э.Г., Дмитриева Е.Н., Куренный Д., Цыганкова Н.В. Совершенствование модели фликера. – Электричество, 2003, № 2. – С. 17-23.
Куренный Э.Г., Дмитриева Е.Н., Вальков Н.Г. Динамические погрешности осциллографирования электроэнергетических процессов и их коррекция. Энергетика и электрификация, 1997, № 3. – С. 14-28.