Рассматриваемые выше модели справедливы для колебаний давления в реальной системе, если они не превышают расчётных, соответствующих Q-H характеристикам действующего насоса.

        Режим водопотребления завода имеет вероятностный характер со склонностью увеличения (потребления) в период с апреля по сентябрь месяцы. В течение суток расход воды не является также постоянным. Колебания потребления вызывают резкие колебания давления в напорной магистрали, в ряде случаев может превышать допустимые значения механической прочности (на разрыв) труб, что свидетельствует о возникновении явления гидравлического удара, который может иметь характер прямого или непрямого.

        Физической основой гидроудара является возникновение колебаний давления вследствие локального изменения скорости в объёме, который заполнен упругим газом или жидкостью. Скорость распространения волны давления в нелимитированом объёме, что заполнен водой, составляет 1430 м/с. Для стальных трубопроводов общепромышленного назначения с достаточной степенью точности её можно считать равной (1300-1500) м/с (для дальнейших расчётов принимаем с = 1300 м/с). Время, за которое волна пройдет от места возбуждения до места отражения и назад, называется фазой волны и определяется формулой:

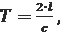                        (9.1)

где l - длина трубопровода между местом возбуждения и местом отражения волны; c - скорость распространения волны.

        Если время, в течение которого осуществляется изменение скорости движения жидкости, равно или меньше фазы волны, то такой удар называется прямым, больше – непрямым.

        Как известно, динамические процессы в трубопроводе с учётом нестационарности течения жидкости описываются двумя основными зависимостями (уравнения гидравлического удара):

уравнение неразрывности потока жидкости:

         (9.2)

уравнение движения для трубопровода с круглым сечением:

   (9.3)

где h - напор; v - скорость течения жидкости в трубопроводе; f - коэффициент Дарси.

        Эти уравнения можно непосредственно проинтегрировать методом конечных разностей, но в этом случае может возникнуть проблема неустойчивости решения.

        Итак, по нашему мнению, лучше находить конечно-разностное решение этих дифференциальных уравнений, приводя их первоначально к характеристической форме. Этот метод известен как метод характеристик. Опуская приведение уравнений гидравлического удара к характеристической форме, запишем:

          (9.4)

        Решение этой системы уравнений определяет скорость движения жидкости и напор в любой точке трубопровода и в любое время. Величиной v можно пренебречь в связи с тем, что v << c . Представим (9.4) в форме, удобной для дальнейших исследований:

           (9.5)

где 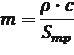- коэффициент связи между приростами расхода и давления в формуле Жуковского; n - гидравлическое сопротивление трубопровода на отрезке dx.

        Рассмотрим интегрирование уравнений гидравлического удара методом характеристик с регулярной сеткой. Этот метод расчёта базируется на том, что трубопровод разбивается на равные отрезки и интегрирование осуществляется через отрезки времени Δt (рис. 9.1), при этом должно выполнятся второе уравнение в (9.5), т.е Δx = c × Δt. Величину Δt выбирают Δt =0,003c, такой шаг интегрирования обеспечивает высокую точность расчёта как гидравлического переходного процесса, так и электромеханического.

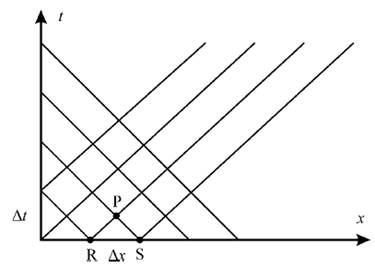
Тогда Δx = c × Δt = 1300 × 0,003 = 3,9 м . Выбранные Δx и Δt достаточно малы, поэтому отрезки характеристик RP и SP можно считать прямыми. Таким образом можно построить линии RP и SP, вдоль которых справедливы два других уравнения:

                           (9.6 a)

вдоль RP

              (9.6 б)

вдоль SP

         (9.6 в)

        Первое из этих двух уравнений справедливо в R и P, второе – в S и P. Таким образом, в точке Р они справедливы одновременно. Запишем (9.6 а) и (9.6 б) в конечно-разностном виде для любой внутренней точки трубопровода: вдоль прямой характеристики:

         (9.7 б)

где p_i и Q_i - давление и расход в i-й точке трубопровода в момент времени t; p_i-1^-t и Q_i-1^-t - давление и расход в i-1 точке трубопровода в предыдущий момент времени t-Δt; p_i+1^-t) и Q_i+1^-t - давление и расход в i+1 точке трубопровода в последующий момент времени t+Δt; Q_cp1,Q_cp2 - средние расходы на отрезке, который прилегает к точке, состояние потока в которой мы рассматриваем, слева и справа соответственно.

        Таким образом, зная состояние потока в трубопроводе в предыдущий момент времени, можно рассчитать состояние потока в момент времени t. Так как Q_cp1,Q_cp2 нам неизвестны, расчёт ведётся с помощью последовательной итерации. Принимаем сразу:

                    (9.8)
                    (9.9)

Разрешая уравнение (5.7 а,б) относительно p_i и Q_i , получим:

   (9.10)
                               (9.11)

Пересчитываем Q_cp1,Q_cp2:

             (9.12)
             (9.13)

        Расчёт по формулам (9.10) – (9.13) повторяем ещё два раза, такого количества итераций достаточно для высокой точности. Таким образом, для каждой внутренней точки можно найти p_i и Q_i.

        На границах имеем только по одной характеристике: на верхнем конце трубопровода – обратная, на нижнем – прямая (см. рис. 9.1). Так как нестационарность возникает на границах, то анализ граничных условий является очень важным. Найдём состояние потока в первой точке трубопровода, которая одновременно является выходной для насоса. Поэтому в качестве второго уравнения возьмём характеристическое уравнение насоса, чем одновременно обеспечивается связь между электромеханической частью насосного агрегата и гидравлической. Совместное решение системы уравнений (6.6) и (9.7 б) даёт:

(9.14)

где            (9.15)

        Найдём состояние потока в последней точке трубопровода, для которой справедлива система, которая состоит из прямой характеристики (9.7 а) и уравнения:

                (9.16)

где p_n,Q_n² - состояние потока на выходе трубопровода.

        Совместное решение системы уравнений (9.16) и (9.7 а) даёт:

(9.17)

где                             (9.18)

        В ходе расчётов состояния потока в первой и последней точках трубопровода пользуемся теми же положениями, что касается Q_cp1 и Q_cp2 при расчётах состояния потока для внутренних точек.

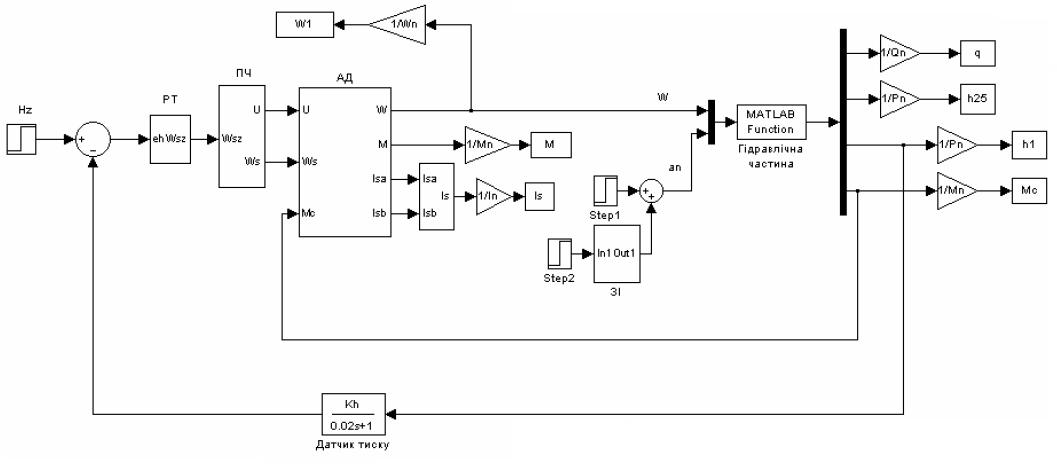
        На рис. 9.2 представлена модель электромеханической системы ПЧ - АД с к.з.р. – насос – трубопровод с учётом нестационарного течения жидкости в трубопроводе. В этой модели гидравлические процессы, которые имеют место в насосе и трубопроводе рассчитываются по уравнениям (6.6), (6.7), (9.8) – (9.18) с помощью MATLAB Simulink Function с условным названием «Гидравлическая часть». Для обратной связи по давлению используется давление в первой точке трубопровода, статическая нагрузка на валу двигателя, а также КПД насоса, который рассчитывается для той же точки, что одновременно является выходной для насоса.

        При моделировании, во-первых, реализуется пуск насоса на заполненный горизонтальный трубопровод. Нами принято, что после разгона в момент времени t = 1,3 c моделируется наброс возмущающего воздействия в виде изменения гидравлического сопротивления насадки (при моделировании прямого гидроудара на вход системы подаётся скачкообразный наброс, непрямого – гидравлическое сопротивление возрастает линейно за время, которое не превышает фазу волны).

        Вследствие резкого увеличения a_H в гидравлической системе возникает гидроудар. В случае прямого гидроудара уменьшение потребления приблизительно в два раза провоцирует появление волны давления, которая превышает номинальное давление насоса более чем на 87%, в случае непрямого – на 28% (нерегулируемый электропривод). Использование регулируемого электропривода по системе ПЧ-АД несколько снижает амплитуду волны (до 80% и 25% соответственно) за счёт снижения частоты вращения рабочего колеса насоса при стабилизации давления. Можно констатировать, что при принятой длине трубопровода ( L = 100 м ), регулируемый электропривод имеет невысокие демпфирующие свойства в плане сглаживания амплитуды гидроудара (вследствие того, что электромеханическая постоянная времени значительно выше фазы волны).