Статья анализирует методы численного решения различных задач, определенных в рамках предельно-начальных значений дифференциальных или интегральных уравнений. В естественных науках и технике, математическая модель в основном определена дифференциальными уравнениями, которые могут быть решены, используя главным образом:
- метод конечных дифференциалов (FDM),
- метод конечных элементов (FEM),
- метод граничных элементов (BEM).

Выбор метода вычисления зависит от многих факторов. Прежде всего, это возможность точного определения задачи и отношения к предельно-начальным условиям. Это также зависит от системы алгебраических уравнений и параметров компьютерной техники, используемой для того, чтобы выполнить задачу.

FDM - самый старый, самый простой, и самый популярный метод, основанный на замене производных конечными разностями. Он был сформулирован как приближенный дискретный метод для решения задач нахождения предельных значений, определенных в условиях дифференциальных уравнений. Кроме того, его применение было расширено на вариационные задачи. Он может также быть применен к задачам с предельно-начальными условиями, связанными с дифференциальными уравнениями параболического типа, описывающими температурное распределение в теории проводимости высоких температур.

Однако, для областей комплексной геометрии, становится слишком сложным определение предельно-начальных условий. Этих трудностей можно избежать, если делать вычисления методом FEM.

Этот метод применяется главным образом к эллиптическим уравнениям. Однако, когда введен шаг дискретизации относительно времени, он может также использоваться для параболических уравнений. Уравнение дискретизируется делением исследуемой области на отдельные треугольники, то есть триангулируется. Затем формулируются основные фунцкии. FEM требует явного определения в анализируемой области. Поэтому обычно применяется для решения внутренних задач. Он может использоваться для решения внешних задач, но это приводит к составлению огромных систем уравнений, поскольку элементы должны покрыть всю область анализа.

Недавно подход BEM очень часто использовался для задач механики. Это помогает значительно сократить количество уравнений. Это достаточно выгодно, так как решение большого количества уравнений требует огромного объема памяти для вычислений и отнимает много времени. Успех метода основан на исключении дискретизации области. Только ее граница подвергается дискретизации, вызывая уменьшение объема памяти и сокращая время вычисления. Подходы FEM и BEM можно считать взаимодополняющими, так как их ошибки, и преимущества компенсируют друг друга. Была проведена обширная работа по объединению этих двух подходов, созданы гибридные методы, комбинирующие преимущества обоих и устраняющие их ошибки.

К сожалению, вышеупомянутые методы малопригодны для определении распределения градиента напряжения в электрических системах. Метод интегральных уравнений (IEM) лучше всего подходит для этой цели, поскольку электрическое потенциальное распределение описывается с помощью интегральных уравнений. Такая формулировка проблемы, включая предельные условия (потенциалы для проводников или их полные сопротивление) приводит к системе интегральных уравнений, численное решение которых позволяет определить распределение плотности сопротивления проводящих частей и потенциального распределения в окружающей среде. Вообще, IEM непосредственно приводит к математической модели, описанной различными классами интегральных уравнений или, косвенно, к дифференциальным уравнениям некоторых предельно-начальных задач. Метод применен к теории проводимости высокой температуры и к теории диффузии. Этот метод также используется в теории электромагнитного поля, например в определении выбранных электродинамических параметров в системах с тремя фазами. Выбор метода в таком случае оправдан, поскольку распределение плотности потока в проводниках фазы получено, решая систему интегральных уравнений. Распределение плотности потока одиночного проводника, описанного было найдено с использованием геометрии системы. Корень уравнения был получен с учетом скин-эффекта проводников фазы, их приближения, потоков утечки в поле. С таким подходом были получены решения, которыми можно воспользоваться, для анализа электромагнитных явлений, происходящие в проводнике и окружающем пространстве, ограничивая рассмотрение к определенной части исследуемого поля, то есть к площади поверхности одиночного проводника. У попыток объединения уравнений электромагнитного поля долгая история, отмеченная большим количеством публикаций. Комплексное представление уравнений поля служит основанием для многих исследований, использующих численные методы, особенно в неограниченных областях.

Цель этой статьи состоит в том, чтобы представить преимущества метода интегральных уравнений (IEM) и возможностей его применения в различных областях техники, в частности, в электротехнике . Это - аналитический численный метод, и он требует больших усилий от высококвалифицированных специалистов (математики, программисты, инженеры). IEM - естественный метод, особенно в области электродинамики. Это относится к случаю электромагнитной области, описываемой интегральными уравнениями, корни которых находятся интегральными преобразованиями в области глобальных переменных, в то время как во временном интервале ожидаемый ответ системы имеет вид интегральных формул. Кроме того, интегральное представление электромагнитного поля в окружающей среде, неоднородной относительно электрических и магнитных составляющих. Здесь ограничивается предполагаемое решение, действительное для целой области, к предопределенной части глобального объекта анализа. Это позволяет значительно сократить размер системы уравнений. Метод стоит того, чтобы быть примененным, в случае задач комплексной геометрии, которые часто встречаются. В таком случае минимизация размера систем уравнений и сокращения времени вычисления при поддержании достаточной точности, становится очень важной.

Интегральные уравнения, или скорее их системы, часто соотносятся с математическими моделями, описывающими распределение плотности потока в поперечном сечении рабочего проводника или в патроне индукционного нагревателя. Знание распределения плотности потока может быть базой для определения некоторых электродинамических параметров, таких как электромагнитная индукция или распределение электродинамических сил, действующих в выбранных точках проводников.

Точно так же уравнения Максвелла, описывающие отношения между векторами электромагнитных полей, представляют собой систему частичных дифференциальных уравнений, которые могут быть преобразованы в интегральные уравнения.

Последующие рассмотрения мы ограничиваем следующими интегральными уравнениями смешанного типа

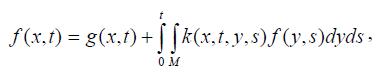
которые обобщают интегральные уравнения Volterra и Fredholm. Представленные уравнения играют очень важную роль в эпидемиологии, механике, теории электромагнитного поля и технике. Эти уравнения также применяются в теории проводимости высокой температуры и математическом моделировании пространственно-временного развития эпидемии. Распространение болезни среди населении может быть описано следующими смешанными интегральными уравнениями. Некоторые начальные краевые задачи для частичных дифференциальных уравнения в физике приводимы к вышеупомянутому интегральному уравнению. Рассмотрим это уравнение в пространстве-времени, где g - данная функция в области D = М'[0, T] (М является компактным подмножеством m-мерного Евклидова пространства), и u - неизвестная функция в D. Корень k определен в области

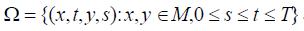
Теория и вычислительные методы были представлены. В следующей секции мы представим испытательный пример для методик проектирования.

Численные эксперименты

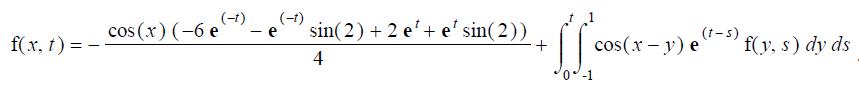
Заключение

Цель этой статьи состоит в том, чтобы показать преимущество метода интегральных уравнений в электротехнике.

Литература

1. Hacia, L.: Metody przyblizonego rozwiazywania pewnych typуw rownan calkowych oraz nierownosci calkowe i ich zastosowania, Rozprawy 367, WPP, Poznan 2002.

2. Hacia, L.: Some integral mathematical models in electrotechnics, Computer Applications in Electrical Engineering-Monograph 1(2004),106-123, WPP, Poznan 2004.

3. Kersner, Z.-Kohut, J.-Moll, I.-Dolezal, D.: Problemy modelovani realnych vztahu v technologii betonu, Kniznice odbornych a vedeckych spisu VUT v Brne, B-133(1991), 109-118, Brno 1998.

4. Moll, I.: On a Linear Differential Equation with Constant Coefficients, Fasciculi Mathematici, 18(1988), 43-50, Poznan 1988.

5. Moll, I.-Zak, J.: Aproximace funkce dotvarovani pocatecnimi cleny Dirichletovy rady s vypoctem exponentu baze, Stavebnicky casopis, 9(1990), 665-67, Bratislava 1990.

6. Nawrowski, R.- Pabian, J.: Obliczanie rozkladu gestosci pradu w przewodach metoda rownan calkowych Fredholma, VII. Konferencja – Zastosowanie Komputerow w Elektrotechnice, Poznan/Kiekrz, 22 – 24.04.2002, 183-186.

7. Piskorek, A.: Rownania calkowe, WNT, Warszawa, 1997.

8. Szymanski, G.: Zastosowanie metod calkowych w elektrodynamice technicznej, Rozprawy 144, WPP, Poznan 1983.