Cтатья подготовлена для публикации в научно-техническом сборнике «Золотая осень», Донецк, 2007 год

УДК 621.316.9

О РАЗВИТИИ МЕТОДИКИ РАСЧЕТНОЙ ОЦЕНКИ БЕЗОПАСНОСТИ ЭЛЕКТРИЧЕСКОГО ИСКРЕНИЯ ВО ВЗРЫВООПАСНОЙ СРЕДЕ



И.А.Бершадский, ДонНТУ, кафедра «Электроснабжение предприятий и городов», З.М. Иохельсон, МакНИИ, отдел электрооборудования, Бондаренко Т.А., магистрантка ДонНТУ


     Постановка задачи. Использование искробезопасного исполнения электрических цепей является одним из основных способов предотвращения аварий, могущих повлечь опасность для жизни человека на взрывоопасных производствах [1]. Искробезопасная электрическая цепь (ИБЦ) определяется как цепь, в которой разряды или термическое действие, возникающее в нормальном и аварийном режимах работы электрооборудования, не вызывает зажигание метано-воздушной смеси (МВС).
     Основным предметом теории ИБЦ является связь между параметрами цепи и воспламеняющей способностью разрядов при ее коммутации. Эта связь определяется переходным процессом в цепи, газовым разрядом, процессом нагрева и горения взрывчатой атмосферы. Сложность этих явлений не позволила до настоящего времени установить с достаточной для практики точностью математическую модель указанных процессов, поэтому методы оценки искробезопасности базируются либо на экспериментальных характеристиках, либо на допущениях далеких от данных по воспламенению.
     В настоящее время принято считать [2], что взрыв газа электрической искрой происходит в результате воздействия тепловой энергии разряда на газовую смесь. Согласно тепловой теории зажигания, весь газ может быть воспламенен, если его элементарный объем будет нагрет до температуры воспламенения Tвосп. Весь окружающий разряд взрывчатый газ воспламенится, если даже источник зажигания прекратит свое существование после воспламенения элементарного объема.
     Цель статьи – предложить математическую модель электрического зажигания метано-воздушной смеси от искрового источника в виде цилиндра с учетом температуры очага разряда, его размеров и средней мощности, зависимости теплофизических параметров газовой среды от температуры, а также влияния электродов на формирование фронта пламени.
     Основные принципы и соотношения. В рамках тепловой теории воспламенения её строгая математическая формулировка должна базироваться на одновременном учете явлений теплопроводности и диффузии при наличии экзотермической химической реакции окисления МВС [3]:

(1)


где – теплоемкость, плотность и коэффициент теплопроводности газовой смеси;T– температура газовой среды в точке пространства, окружающей или принадлежащей стволу электрического разряда; q– тепловая энергии, выделяемая в результате реакции сгорания грамм-моля горючего; – скорость реакции; – предэкспоненциальный множитель и порядок реакции; Е – энергия активации реакции окисления (сгорания) газовой смеси; R = 8,31 Дж/моль·К – универсальная газовая постоянная; D – коэффициент диффузии горючего газа в зоне реакции его окисления; с – концентрация метана в воздухе; P0 – удельная объемная мощность искрового разряда.
     Решение этой системы уравнений в общем виде не найдено из-за возникающих математических трудностей [3, 4]. Однако, современный уровень компьютерных технологий позволяет эффективным образом получать приближенные решения таких задач в многомерной, нелинейной и нестационарной постановке [5].

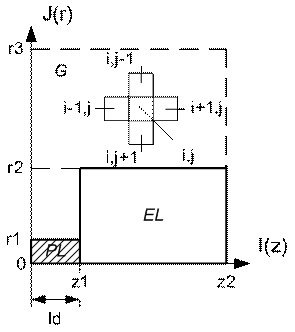
Рисунок 1 – Аппроксимация моделируемого пространства (PL - ствол разряда, EL - электрод, G - горючая газовая смесь)

Рисунок 1 – Аппроксимация моделируемого пространства (PL - ствол разряда, EL - электрод, G - горючая газовая смесь)

     Реальный тепловой источник при электрическом зажигании может моделироваться в виде цилиндра, опирающегося торцами в расходящиеся электроды. В процессе моделирования предполагается, что электроды имеют ось симметрии и плоскость симметрии, перпендикулярную этой оси и равноудалённую от торцов электродов. Таким образом при расчете температурного поля рассматривается только один квадрант плоскости, в которой расположена ось симметрии (рис. 1).
     Учитывая указанную конфигурацию модели, систему дифференци-альных уравнений в частных производных удобно описывать в 2-х мерной цилиндрической системе координат (ЦСК) (z, r).
     Для разработки модели электрического зажигания газовой смеси система (1) модифицируется к более удобному для численных решений виду:

, (2)

     где q – мощность теплового источника экзотермической реакции; η – доля выгоревшего метана по отношению к его начальной концентрации; P0 – мощность электрического разряда.
     Воспользовавшись формулами для представления дифференциального уравнения теплопроводности в ЦСК [6] и, учитывая осевую симметрию задачи, получим:

(3)

     где i, j – номера координат по оси z и радиусу r; τ – шаг по времени (определяется, исходя из условий устойчивости и монотонности разностного решения задачи [5]); – шаг по радиусу и оси цилиндрической системы координат; a(T) – коэффициент температуропроводности; m=k или k+1 – номер временного слоя, выбор которого пояснён ниже; q – функция источника, учитывающая одновременное выделение тепла в экзотермической реакции и плазме дуги.
     Разностная схема (3) – неявная, то есть для получения температуры на следующем временном слое необходимо решить систему уравнений методом прогонки. Здесь необходимо учесть, что требуется решать двухмерную задачу и приходится использовать одну из т.н. «экономичных» схем, а именно локально-одномерную с расщеплением по отдельным координатам z, r [5].
     В процессе развития ядра пламени происходит изменение температуры газа и соответствующее изменение объема очага. Чтобы учесть это явление взрывоопасная газовая смесь рассматривается как идеальный газ для которого (p, V, T – давление, объем, температура), и вводится, согласно [7], относительная объемная концентрация одного из реагирующих компонентов:

, (4)

где x,xo – мгновенное и начальное абсолютные объемные концентрации.
     Тогда при допущении p=const:

, (5)

где - значения при T1 и T2.

     В разностной форме (4) примет вид:


, , (6)

где – изменение относительной концентрации при изменении T на .
     Пренебрегая третьим слагаемым: или

, (7)

где– доля использованного (выгоревшего) компонента.
     Уравнение (3), записанное в разностной форме:

, (8)

где [7] – константа, учитывающая конечность скорости движения газа; k – номер текущего шага по времени.

     Моделирование условий воспламенения метановоздушной смеси. Температура пламени, характеризующая опасный и безопасный процесс искрообразования, просчитывается с использованием рассмотренной выше модели. Вначале не учитывается наличие электродов, и определяется энергетическая зона возникновения устойчивого фронта пламени с температурой горения МВС 2137 К, а также зона его разрушения (см. рис. 2 а, б).
     Затем, для оценки изменения агрессивности разряда под действием электродов рассматривается влияние их диаметра и длины межконтактного промежутка на энергию зажигания.

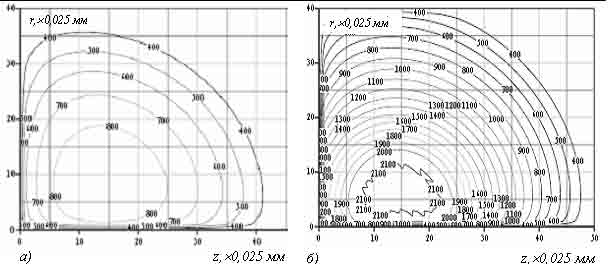
Изолинии температуры при зажигании МВС (электрод отсутствует)

Рисунок 2 – Изолинии температуры при зажигании МВС (электрод отсутствует)
а) tp=100 мкс, Р0 = 2,4 Вт, время наблюдения – 500 мкс (устойчивый фронт пламени не возник)
б) tp=100 мкс, Р0 = 2,5 Вт, время наблюдения – 500 мкс (устойчивый фронт пламени возник)


Изолинии температуры при зажигании МВС (с электродом)

Рисунок 3 – Изолинии температуры при зажигании МВС (с электродом)
а) «тонкий электрод», tp=100 мкс, Р0 = 5 Вт, r1=0.13 мм, r2=0.25 мм, r3=1мм, z1=0.25 мм, z2=1.25 мм;
время наблюдения – 500 мкс (устойчивый фронт пламени возник)
б) «толстый электрод», tp=100 мкс, Р0 = 12 Вт, r1=0.18 мм, r2=0.5 мм, r3=2 мм, z1=0.25 мм, z2=1.25 мм;
время наблюдения – 500 мкс (устойчивый фронт пламени возник)

     Характер распространения очага пламени при медленно расходящих-ся электродах, т.е. в условиях, когда их воздействие значительно, меняется (см. рис. 3 а, б). Это объясняется усилением факторов, препятствующих воспламенению:
     – увеличение потерь энергии в результате роста кривизны пламени и потери энергии в контактах;
     – частичное «экранирование» контактами поступления свежей горючей смеси в очаг зажигания;
     – несовпадение во времени максимального воспламеняющего значения мощности и расхождения контактов на достаточное расстояние, при котором их влияние уменьшается.
     Сравнение рис. 3 а и б показывает также различие энергий зажигания в зависимости от радиуса электродов r2: она возрастает с 0,5 мДж при r2=0,25 мм («тонкий электрод») до 1,2 мДж при r2=0,5 мм («толстый электрод»). Зависимость минимальной энергии зажигания Wmin от радиуса электрода r2 при разных длинах межконтактного промежутка z1 приведена на рис. 4.

Зависимость энергии зажигания МВС от радиуса электрода и межконтактного расстояния
Рисунок 4 – Зависимость энергии зажигания МВС от радиуса электрода и межконтактного расстояния


     Выводы:
     1. Предложена математическая модель электрического зажигания МВС от источника постоянной мощности, которая основываясь на решении нестационарного уравнения теплопроводности и диффузии для заданных параметров электрического разряда, искрообразующего механизма и взрывоопасной смеси, может быть использована в дальнейшей расчетной оценке искробезопасности электрических цепей.
     2. Для определенного искрообразующего механизма существует такая мощность источника, при уменьшении которой возникновение взрыва невозможно независимо от времени существования этого источника.
     3. При увеличении диаметра электродов и уменьшения межконтактного расстояния при одном и том же времени существования разряда (100 мкс) возрастает минимальная энергия зажигания.
     4. Разработанная модель имеет преимущества перед известными, так как обладает устойчивостью за счет применения неявной нелинейной разностной схемы, более точна и не требует предварительного подбора коэффициентов модели при изменении расчетных условий.



ЛИТЕРАТУРА

    1. Лейбов Р.М., Озерной М.И. Электрификация подземных горныхработ. М.: Недра, 1972. – 464 с.

    2. Серов В.И. Воспламеняющая способность сложных индуктивных цепей. М.: Наука, 1966. – 95 с.

    3. Хитрин Л.Н. Физика горения и взрыва. М.: МГУ, 1957. – 444 с.

    4. Франц-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. М.-Л.: АНСССР, 1947.- 367 с.

    5. Дульнев Г.Н. и др. Применение ЭВМ для решения задач теплообмена. М.: Высш.шк., 1990. -207 с.

    6. Коздоба Л.А. Вычислительная теплофизика. К.: 1992. ектрическая цепь. Госстандарт России от 09.12.1999 г. – М.: Изд-во стандартов, 1999.

    7. Коган А.Г. Электроизмерительная и расчетная оценка искробезопасности индуктивных электрических цепей на основе математической модели очагового зажигания рудничных газов: Автореф. дис … к.т.н. Ма-кеевка: МакНИИ, 1988.
Назад