Постановка проблемы. Использование алгоритмов скалярного частотного управления (ЧУ) является весьма распространенным на практике для электроприводов (ЭП) машин, к которым предъявляют жесткие требования к статическим параметрам (жесткости механических характеристик, перегрузочной способности) при невысоких требованиях к качеству переходных процессов. К их числу могут быть отнесены краны, насосы, подъемные установки, различные механизмы промышленного транспорта. Наибольшее распространение в системах скалярного ЧУ ввиду его удобства получил закон управления, обеспечивающий в некотором диапазоне регулирования частоты примерное постоянство потокосцепления статора асинхронного двигателя (АД) –  , достигаемый за счет компенсации падения напряжения в активном сопротивлении обмотки статора (так называемая IR-компенсация). Диапазон регулирования частоты вращения в таких ЭП вниз от номинальной ограничен из-за возникающего при этом насыщения магнитной цепи двигателя и, как правило, не превышает отношения (3…5):1 [1].
, достигаемый за счет компенсации падения напряжения в активном сопротивлении обмотки статора (так называемая IR-компенсация). Диапазон регулирования частоты вращения в таких ЭП вниз от номинальной ограничен из-за возникающего при этом насыщения магнитной цепи двигателя и, как правило, не превышает отношения (3…5):1 [1].
Диапазон регулирования можно расширить за счет поддержания постоянства магнитного потокосцепления АД в воздушном зазоре  . В современных комплектных ЭП предусмотрена возможность задания отдельных точек закона ЧУ (вольт-частотной характеристики) для последующей его линейной интерполяции, что позволяет обеспечить требуемые жесткость характеристик и перегрузочную способность АД для конкретного применения ЭП.
. В современных комплектных ЭП предусмотрена возможность задания отдельных точек закона ЧУ (вольт-частотной характеристики) для последующей его линейной интерполяции, что позволяет обеспечить требуемые жесткость характеристик и перегрузочную способность АД для конкретного применения ЭП.
Анализ исследований и публикаций. Основные соотношения для координат и параметров АД, позволяющие определить рациональные способы ЧУ двигателем, приведены в [2]. Там же показана общая зависимость для магнитного потока, которая позволяет оценить степень его увеличения при снижении частоты (в области насыщения магнитной цепи АД). Достаточно полный обзор законов ЧУ, имеющий в настоящее время практическое применение, выполнен, в частности, в [1, 3]. При этом, однако, отсутствуют практические рекомендации для расчета зависимости амплитуды подводимого к статору АД напряжения в функции его частоты для реализации закона  , который позволит улучшить качество статических характеристик ЭП в области низкой частоты и расширить диапазон регулирования.
, который позволит улучшить качество статических характеристик ЭП в области низкой частоты и расширить диапазон регулирования.
Цель статьи. Вывод аналитических выражений для закона ЧУ  , позволяющих дать практические рекомендации для настройки преобразователя частоты (ПЧ). Анализ динамических характеристик частотно-регулируемого АД с целью определения факторов, ограничивающих применение подобного регулирования на низкой частоте.
, позволяющих дать практические рекомендации для настройки преобразователя частоты (ПЧ). Анализ динамических характеристик частотно-регулируемого АД с целью определения факторов, ограничивающих применение подобного регулирования на низкой частоте.
Результаты исследований. При математическом описании процессов в АД приняты допущения о его строгой симметричности, синусоидальности всех электромагнитных величин, отсутствии влияния пазов статора и ротора, отсутствии потерь в стали статора и ротора и сосредоточенности параметров обмоток. Считается, что значения параметров ротора приведены к обмотке статора.
Все параметры и координаты АД рассматриваются в относительных единицах. В качестве базисных параметров приняты:
– 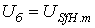 – амплитуда номинального фазного напряжения статора;
– амплитуда номинального фазного напряжения статора;
–  – амплитуда номинального фазного тока статора;
– амплитуда номинального фазного тока статора;
–  – номинальная угловая частота напряжения сети;
– номинальная угловая частота напряжения сети;
– время 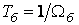 – величина, обратная базисной частоте;
– величина, обратная базисной частоте;
– потокосцепление  ;
;
– сопротивление 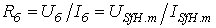 ;
;
– индуктивность 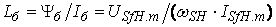 .
.
В качестве исходных рассматриваются уравнения Парка – Горева, записанные в ортогональной системе координат x, y, вращающейся относительно неподвижного статора с синхронной угловой частотой
где 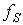 – заданная частота напряжения статора.
– заданная частота напряжения статора.
Уравнения электрического равновесия цепей статора и ротора имеют вид
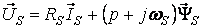 |
(1) |
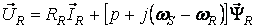 |
(2) |
где 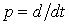 – оператор дифференцирования;
– оператор дифференцирования;
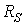 – активное сопротивление обмотки фазы статора;
– активное сопротивление обмотки фазы статора;
 – электрическая частота вращения ротора.
– электрическая частота вращения ротора.
Вектор главного магнитного потокосцепления АД (потокосцепления в воздушном зазоре) равен
 |
(3) |
где 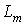 – главная взаимная индуктивность между фазой статора и фазами ротора.
– главная взаимная индуктивность между фазой статора и фазами ротора.
Уравнения для потокосцеплений статора и ротора
 |
(4) |
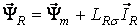 |
(5) |
где 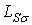 ,
, 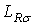 –индуктивности рассеяния статора и ротора.
–индуктивности рассеяния статора и ротора.
Из уравнений (1) – (5) можно получить выражение в общем виде, отражающее связь между вектором напряжения, приложенного к статору, и вектором главного магнитного потокосцепления АД
где 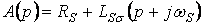 ,
, 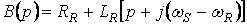 ,
,
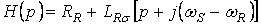 – степенные полиномы с переменными коэффициентами, зависящими от электрической частоты вращения полей статора
– степенные полиномы с переменными коэффициентами, зависящими от электрической частоты вращения полей статора  и ротора
и ротора  ;
;
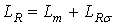 – полная индуктивность ротора.
– полная индуктивность ротора.
Для частотно-регулируемого короткозамкнутого АД ( ) уравнение (6) после преобразований можно представить в виде
) уравнение (6) после преобразований можно представить в виде
 |
(7) |
где  ;
;
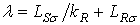 ; ;
; ; 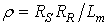 ;
;
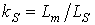 ,
, 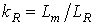 – коэффициенты электромагнитной связи статора и ротора;
– коэффициенты электромагнитной связи статора и ротора;
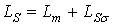 – полная индуктивность статора
– полная индуктивность статора
 .
.
Уравнение, записанное для модулей величин и являющееся частным случаем (7), представлено в [2], однако там не выполнено анализа полученной зависимости на предмет применения к закону  . К тому же, записанная для модулей величин зависимость не позволяет оценить динамические свойства АД при указанном управлении.
. К тому же, записанная для модулей величин зависимость не позволяет оценить динамические свойства АД при указанном управлении.
На основании (7) с использованием уравнения (2) можно получить выражение для потокосцепления статора
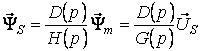 |
(8) |
где  ;
; 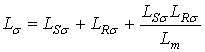 .
.
Анализ выражения (8) теоретически позволяет оценить запас для расширения диапазона регулирования частоты за счет использования закона управления  вместо закона
вместо закона  . В частности, если
. В частности, если  , этот запас выражается величиной, обратной значению коэффициента электромагнитной связи статора
, этот запас выражается величиной, обратной значению коэффициента электромагнитной связи статора 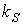 .
.
С помощью (8) при принятии допущения о постоянстве частоты вращения ротора ( ) может быть оценен характер электромагнитных переходных процессов в АД на основании аналитического либо численного решения характеристического уравнения
) может быть оценен характер электромагнитных переходных процессов в АД на основании аналитического либо численного решения характеристического уравнения
Дальнейшие исследования проводятся на примере двигателя 4А-112-М4 (5,5 кВт; 1448 об/мин; 380 В; 10,4 А).
Графики корней 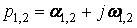 уравнения (9), рассчитанные при
уравнения (9), рассчитанные при 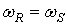 , представлены на рисунке 1. Таким образом, интенсивность затухания колебаний, вызванных действием возмущающих факторов (например, изменением напряжения сети, момента сопротивления на валу АД), оцениваемая по значению
, представлены на рисунке 1. Таким образом, интенсивность затухания колебаний, вызванных действием возмущающих факторов (например, изменением напряжения сети, момента сопротивления на валу АД), оцениваемая по значению  меньшей по абсолютному значению действительной части одного из корней (
меньшей по абсолютному значению действительной части одного из корней ( ), существенно снижается в области низкой частоты.
), существенно снижается в области низкой частоты.

Рисунок 1 – Корни 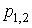 характеристического уравнения (9) при характеристического уравнения (9) при 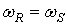 |
Абсолютное скольжение 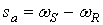 практически влияет только на частоту
практически влияет только на частоту  и
и  свободных колебаний. При этом
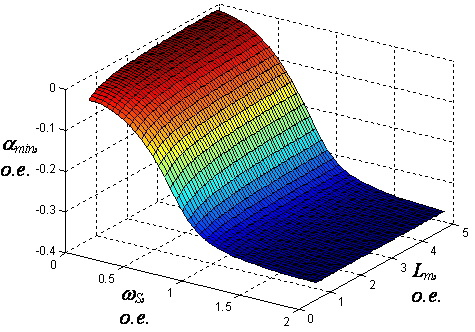
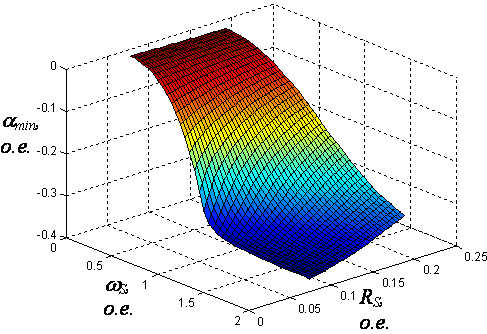
свободных колебаний. При этом  зависит от значений активных сопротивлений статора и ротора (определяемых тепловым состоянием их обмоток) и главной взаимной индуктивности (изменяющейся вследствие нелинейности магнитной цепи АД). Анализ соответствующих зависимостей (рисунок 2) позволяет сделать вывод о дополнительном снижении интенсивности затухания при низкой температуре обмоток АД (близкой к практически холодному состоянию), а также при больших значениях индуктивности
зависит от значений активных сопротивлений статора и ротора (определяемых тепловым состоянием их обмоток) и главной взаимной индуктивности (изменяющейся вследствие нелинейности магнитной цепи АД). Анализ соответствующих зависимостей (рисунок 2) позволяет сделать вывод о дополнительном снижении интенсивности затухания при низкой температуре обмоток АД (близкой к практически холодному состоянию), а также при больших значениях индуктивности 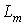 (при ослаблении поля вследствие некорректного задания закона ЧУ), особенно при низкой частоте
(при ослаблении поля вследствие некорректного задания закона ЧУ), особенно при низкой частоте 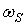 напряжения статора.
напряжения статора.
 а)
а)
 б)
Рисунок 2 – Зависимости, отражающие влияние изменения параметров Lm (а) и RS (б) двигателя на интенсивность затухания переходных процессов
б)
Рисунок 2 – Зависимости, отражающие влияние изменения параметров Lm (а) и RS (б) двигателя на интенсивность затухания переходных процессов |
Указанные закономерности справедливы при произвольном законе ЧУ, однако при  это обстоятельство может служить ограничением при регулировании частоты в области малых значений.
это обстоятельство может служить ограничением при регулировании частоты в области малых значений.
Рассмотрим (8) применительно к установившимся режимам для определения зависимости  , позволяющей реализовать закон
, позволяющей реализовать закон  . Положив
. Положив  , можно записать
, можно записать
Вынеся в знаменателе  как общий множитель, последнее выражение запишем в виде:
как общий множитель, последнее выражение запишем в виде:
Обозначив 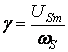 , для модулей векторов можно записать
, для модулей векторов можно записать
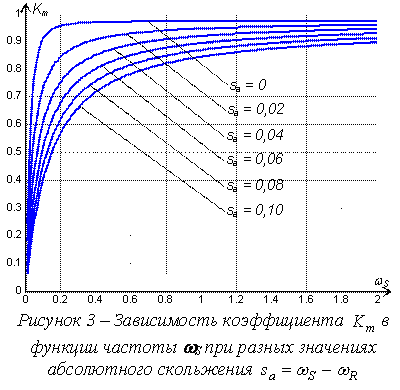
Последнему выражению соответствуют графические зависимости, представленные на рисунке 3 для разных значений абсолютного скольжения 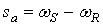 . Зависимости следует рассматривать с учетом того, что при
. Зависимости следует рассматривать с учетом того, что при 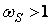 дальнейшее повышение частоты выполняется при неизменном напряжении, равном номинальному (
дальнейшее повышение частоты выполняется при неизменном напряжении, равном номинальному ( ).
).
 |
Исследования показали, что ни изменение активных сопротивлений двигателя, ни изменение главной взаимной индуктивности не оказывают значимого влияния на значение коэффициента Km. Следовательно, зависимость для закона управления, позволяющего обеспечить 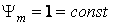 , может быть определена как обратная зависимость по отношению к изображенной на рисунке 3, умноженная на текущее значение заданной частоты (рисунок 4).
, может быть определена как обратная зависимость по отношению к изображенной на рисунке 3, умноженная на текущее значение заданной частоты (рисунок 4).
Анализ представленных зависимостей показывает, что в зависимости от жесткости характеристик АД для реализации закона  в зоне номинальной частоты требуемая амплитуда напряжения статора может превышать номинальное напряжение на 10…20%. Это, с одной стороны, требует применения ПЧ с соответствующим запасом по напряжению, а с другой стороны, велика вероятность возникновения насыщения зубцовой зоны статора из-за увеличения потокосцепления статора
в зоне номинальной частоты требуемая амплитуда напряжения статора может превышать номинальное напряжение на 10…20%. Это, с одной стороны, требует применения ПЧ с соответствующим запасом по напряжению, а с другой стороны, велика вероятность возникновения насыщения зубцовой зоны статора из-за увеличения потокосцепления статора 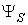 . В области низкой частоты такой закономерности не наблюдается, однако как было показано выше, имеет место существенное снижение интенсивности затухания переходных процессов как при изменении нагрузки, так и при колебаниях напряжения сети. Указанные обстоятельства служат ограничением для применения рассматриваемого закона ЧУ.
. В области низкой частоты такой закономерности не наблюдается, однако как было показано выше, имеет место существенное снижение интенсивности затухания переходных процессов как при изменении нагрузки, так и при колебаниях напряжения сети. Указанные обстоятельства служат ограничением для применения рассматриваемого закона ЧУ.
Таким образом, закон позволяет обеспечить достаточно качественные статические и динамические характеристики ЭП в сре днем диапазоне частоты
днем диапазоне частоты  , который ограничивается сверху условиями недопустимого возрастания потокосцепления статора
, который ограничивается сверху условиями недопустимого возрастания потокосцепления статора 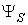 , а снизу – недопустимым снижением интенсивности затухания электромагнитных переходных процессов.
, а снизу – недопустимым снижением интенсивности затухания электромагнитных переходных процессов.
Выводы:
1. Получена в аналитическом виде зависимость между модулями вектора  напряжения, приложенного к статору, и вектора
напряжения, приложенного к статору, и вектора 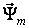 главного магнитного потокосцепления АД, которая использована для определения необходимого закона изменения заданной амплитуды напряжения статора в функции заданной частоты, используемого при реализации закона
главного магнитного потокосцепления АД, которая использована для определения необходимого закона изменения заданной амплитуды напряжения статора в функции заданной частоты, используемого при реализации закона  , а также анализа динамических свойств АД при указанном управлении.
, а также анализа динамических свойств АД при указанном управлении.
2. Установлены зависимости интенсивности затухания переходных процессов от частоты напряжения статора АД, а также от значений активного сопротивления статора и ротора и главной взаимной индуктивности. Имеет место дополнительное снижение интенсивности затухания переходных процессов при практически холодном состоянии обмоток АД, а также при ослаблении поля, которое особенно заметно при низкой частоте напряжения, прикладываемого к обмоткам статора.
3. Закон  позволяет обеспечить достаточно качественные статические и динамические характеристики ЭП в среднем диапазоне частоты, который ограничивается сверху условиями недопустимого возрастания потокосцепления статора, а снизу – недопустимым снижением интенсивности затухания электромагнитных переходных процессов.
позволяет обеспечить достаточно качественные статические и динамические характеристики ЭП в среднем диапазоне частоты, который ограничивается сверху условиями недопустимого возрастания потокосцепления статора, а снизу – недопустимым снижением интенсивности затухания электромагнитных переходных процессов.
4. Целесообразным направлением дальнейших исследований является оценка предпочтительности использования законов скалярного ЧУ для механизмов с известным характером изменения момента сопротивления в функции частоты вращения, а также экспериментальная проверка результатов исследований.
Список литературы
1. Соколовский Г.Г. Электроприводы переменного тока с частотным регулированием: Учебник для студ. высш. учеб. заведений. – М.: Издательский центр «Академия», 2006. – 272 с.
2. Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами: Учеб. пособие для вузов. – Л.: Энергоиздат. Ленингр. отд-ние, 1982. – 392 с.
3. Комплектні електроприводи: Навч. посібник / М.М. Казачковський. – Дніпропетровськ: Національний гірничий університет, 2003. – 226 с.