Введение
Известно, что при питании асинхронного двигателя от несинусоидального источника питания могут возникать определенные проблемы благодаря наличию гармоник в напряжении источника. Например, хорошо известно, что использование шестипульсного инвертора может приводить к возникновению неблагоприятных эффектов, таких как пульсации вращающего момента, сопровождаемые шумом и вибрацией. Однако менее известно, что колебания вращающего момента наряду с помехами могут также присутствовать в случае использования систем электропривода, которые имитируют синусоидальную волну, как например схемы контроля ориентации поля, в случае их входа в режим перемодуляции. Различные методы анализа были предложены для оценки влияния питания двигателя от несинусоидального источника [1–3]. Из них те, которые основаны на частотном анализе, дают результаты, не позволяющие оценить неблагоприятное влияние гармоник при использовании источника с их наличием.
Эта статья предлагает интуитивный подход к анализу неблагоприятных эффектов с особенным акцентом на колебаниях вращающего момента. Подход основан на понятии пространственно-фазового моделирования [4]. Показано, что достаточно хороший результат может быть достигнут в предсказании характера и величины колебаний вращающего момента с помощью использования сравнительно простой модели для анализа во времени.
Основные положения
Как непосредственно фазовые модели [5], так и ортогональные модели (в общем называемые d-q–моделями, основанные на теории Парка о двойном воздействии [6]), были использованы во временном анализе характеристик асинхронных двигателей. Предполагалось, что моделирование многофазных машин стало более корректным, так как непосредственно измеряемые физические величины присутствуют в моделях и влияние асимметрии питания может быть учтено относительно легко. Пространственные векторно-фазовые модели предлагают действительную и интересную альтернативу. Они включают в себя как непосредственные фазовые модели, так и ортогональные модели, выполняя прямой или обратный переход между пространственными векторно-фазовыми моделями и другими возможными. Кроме того, они корректно моделируют вращающееся поле в пределах пространства машины. Поэтому их принятие для моделирования может составлять “интуитивный” подход.
Понятие пространственно-фазового вектора
Переход от прямой фазовой к пространственной векторно-фазовой модели может сопровождаться присвоением “векторных” свойств переменным машины, зависящим от времени. Поэтому сумма токов статора и ротора для трехфазной машины в пространственном векторно-фазовом обозначении примет вид
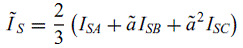 |
(1) |
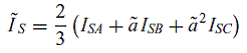 |
(2) |
Фазные напряжения статора также можно выразить через одну пространственно-векторную величину
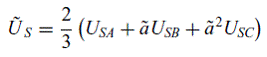 |
(3) |
Подобные рассуждения можно применить для потокосцеплений, а именно
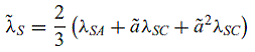 |
(4) |
где
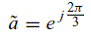 |
(5) |
 |
(6) |
Следует обратить внимание, что комплексный j-оператор использован в качестве единичного пространственно-фазового вектора 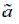 и и 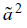 и по своему значению отличается от того, которое используется в анализе электрических цепей: он обозначает пространственный сдвиг величины, с которой он связан. и по своему значению отличается от того, которое используется в анализе электрических цепей: он обозначает пространственный сдвиг величины, с которой он связан.
Уравнения (1)–(4), показывают, что единичный пространственно-фазовый вектор может быть построен на базисах отдельных фазных обмоток многофазной машины. С другой стороны, особенно если осуществляется переход от преобразованной модели, как в случае с ортогональными моделями, суммарные токи статора и ротора в пространственном векторно-фазовом виде могут быть выражены как
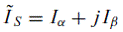 |
(7) |
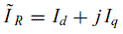 |
(8) |
Подобные рассуждения применимы для фазных напряжений статора и ротора, а также для потокосцеплений
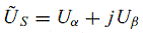 |
(9) |
 |
(10) |
 |
(11) |
 |
(12) |
Модель двигателя
В соответствии с вышеизложенным, может быть разработана пространственная векторно-фазовая модель, описывающая электромагнитное поведение полной машины. Получаем одно уравнение для статорных и одно для роторных обмоток соответственно
 |
(13) |
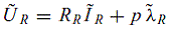 |
(14) |
где 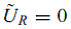 для асинхронного двигателя с короткозамкнутым ротором. Уравнения также могут быть записаны с помощью параметров электрических цепей модели для асинхронного двигателя с короткозамкнутым ротором. Уравнения также могут быть записаны с помощью параметров электрических цепей модели
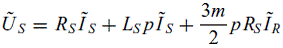 |
(15) |
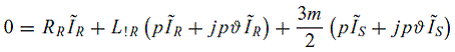 |
(16) |
Вместе с уравнением движения, приведенного ниже, эта достаточно простая модель может быть развернута с целью проведения анализа поведения многофазного асинхронного двигателя во времени.
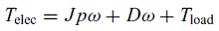 |
(17) |
В уравнениях, приведенных выше, символ р обозначает производную по времени величины, предшествующей ему.
Развиваемый приводом электромагнитный момент может быть получен как:
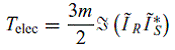 |
(18) |
Модель источника
Если предполагается работа асинхронного двигателя в системе регулирования скорости, несинусоидальный характер питающего напряжения должен быть учтен при моделировании электропривода, чтобы отразить влияние гармонического состава питающего напряжения на характеристику машины. В случае использования в качестве источника напряжения инвертора, выполненного по шестипульсной схеме, который изображен на рис. 1, периодические напряжения UА, UВ, и UС показаны на рис. 2. Цель данных рассуждений сводится к принятию модели инвертора с идеальными ключами. Рисунок 2 иллюстрирует результирующие напряжения на выходах инвертора, подающие “шестипульсные” напряжения на статорные обмотки двигателя.
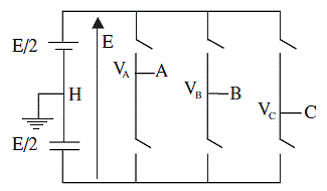
Рисунок 1. Инвертор источника напряжения |

Рисунок 2. Напряжения на выходе преобразователя |
В пространственной векторно-фазовой форме полученные “шестипульсные” напряжения, могут быть удобно получены в виде ортогональных составляющих
 |
(19) |
 |
(20) |
 |
(21) |
Подвергнув  и и 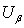 разложению Фурье, получим разложению Фурье, получим
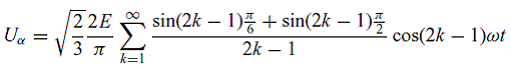 |
(22) |
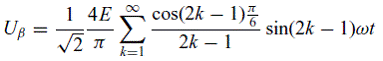 |
(23) |
Очевидно, не все гармоники в (22) и (23) существенны с точки зрения порождения неблагоприятных эффектов. Только те гармоники, которые являются существенными и могут достаточно сильно влиять на характеристики, должны быть учтены в модели источника питания.
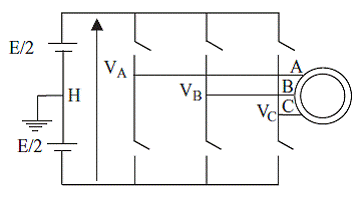 Рисунок 3. Типовой асинхронный привод с инвертором
Рисунок 3. Типовой асинхронный привод с инвертором |
Модель системы управления
Управляемый преобразователем асинхронный двигатель может быть смоделирован объединением пространственной векторно-фазовой модели машины с моделью источника питания, представляющего несинусоидальный инвертор напряжения. Рисунок 3 поясняет полученную в результате модель.
Все электромагнитные величины в (15) и (16) выражены через пространственно-фазовые векторы благодаря переходу от фактической трехфазной модели машины к ортогональной модели с альфа-бета и d-q осями, напряжения и токи которых объединены с целью получения упрощенного представления системы привода. К тому же, становится возможным оценить влияние гармоник источника питания простым добавлением условного источника гармоник в (15).
Результаты моделирования
Смоделированные выходные напряжения альфа-бета, содержащие существенные гармоники, были взяты для дальнейшего моделирования. Колебания вращающего момента вместе с этими напряжениями для состояния без и с нагрузкой показаны на рис. 4 и 5 соответственно, полученные в результате решения системы уравнений (15)-(17).
Результаты моделирования показывают, что колебания вращающего момента уже имеют значительную величину, когда двигатель не нагружен. Под нагрузкой, как видно из рисунка, диапазон колебаний расширяется. Электромагнитные величины, не приведенные здесь, позволяют предположить возможность ухудшения ситуации. Результаты существенны и они показывают, что использованный метод моделирования пригоден для оценки неблагоприятного поведения вращающего момента.
Экспериментальная проверка
Обоснованность подхода была проверена экспериментально на трехфазном асинхронном двигателе мощностью 1,5 кВт, управляемом преобразователем. Использовалось управление ориентацией поля с сильной перемодуляцией, что приводило к появлению гармоник в напряжении источника, характер и величина которых были похожими на аналогичные в случае использования шестипульсного инвертора. Таблица 1 представляет необходимые данные исследуемого двигателя, с использованием которых проводилось моделирование, описанное выше. Рисунок 6 отображает измеренный диапазон колебаний вращающего момента при установившемся состоянии в условиях полной нагрузки. Как видно, характер и относительная величина вращающего момента практически повторяют результаты моделирования. Рисунок 7 показывает колебания вращающего момента без нагрузки. Величина колебаний возросла под нагрузкой в сравнении с холостым режимом – это также наблюдение, подтвержденное моделированием.
Очевидно, простое представление на модели не позволяет точно предсказать колебания момента во всем диапазоне, в том числе измеренные отклонения в колебаниях вращающего момента. Однако достигнутая аппроксимация является удовлетворительной.
Заключение
Интуитивный метод анализа, основанный на понятии пространственно-фазового вектора дает адекватную и точную информацию о характере возможных колебаний вращающего момента в асинхронном двигателе, управляемом с помощью инвертора. Достаточно легко получить вероятные результаты с затратой минимальных усилий на вычисления. Хотя подход был продемонстрирован для привода с шестипульсным инвертором, он также применим к более сложным системам привода.
Ссылки
[1] T. Lipo, P.C. Krause, H.E. Jordan, Harmonic torque and speed pulsations in a rectifier-inverter
induction motor drive, IEEE Trans., Vol. PAS-88, No. 5, pp. 579–587, 1969.
[2] S.T.D. Robertson, K.M. Hebbar, Torque pulsations in induction motors with inverter drives,
IEEE Trans. Ind. Gen. Appl., Vol. IGA-7, No. 2, pp. 318–323, 1971.
[3] G.B. Klimann, A.B. Plunkett, Modulation strategy for a PWM inverter drive, IEEE Trans. Ind.
Appl., Vol. IA-15, No.1, pp. 72–79, 1979.
[4] K.P. Kovacs, J. Racz, Transiente Vorg?ange in Wechselstrommaschinen, Budapest: Academiai
Kiado, 1959.
[5] R.J.W. Koopman, Direct simulation of AC machinery including third-harmonic effects, IEEE
Trans. Power Apparatus Syst., Vol. PAS 88, No. 4, pp. 465–470, 1969.
[6] R.H. Park, Two-reaction theory of synchronous machinery—Part I, AIEE Trans., Vol. 48, pp. 716–730, 1929. |